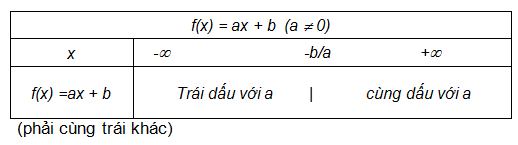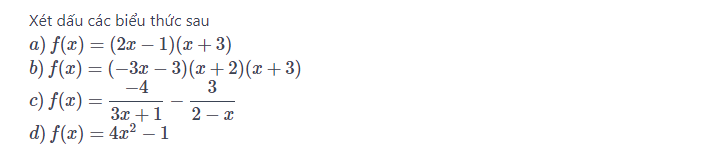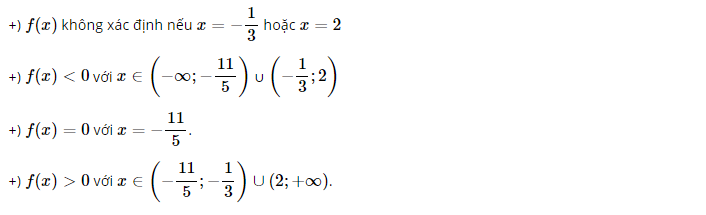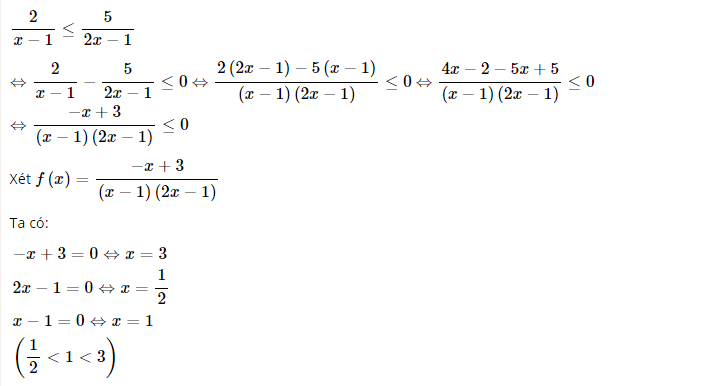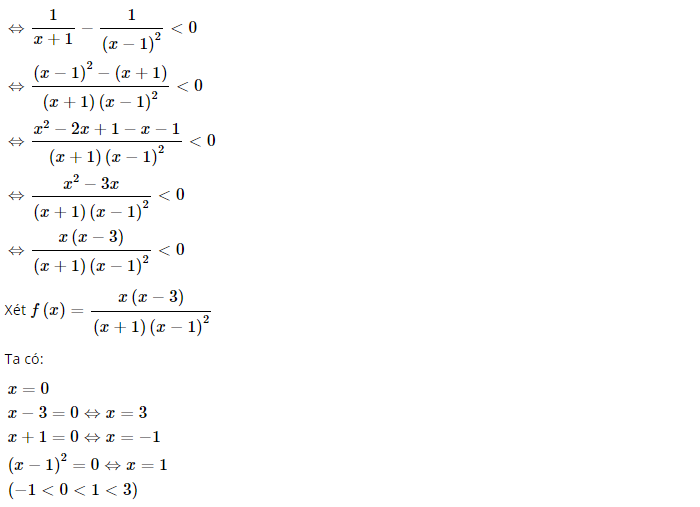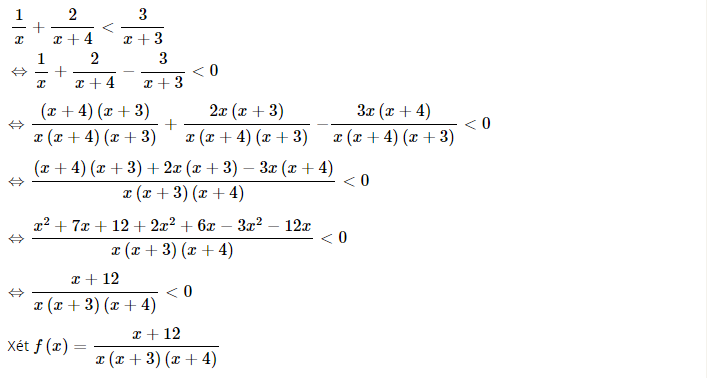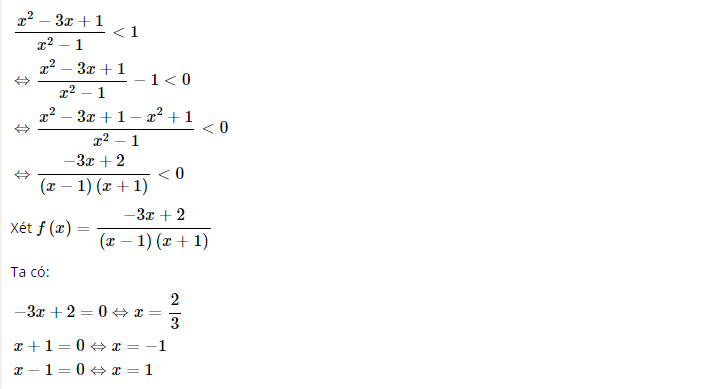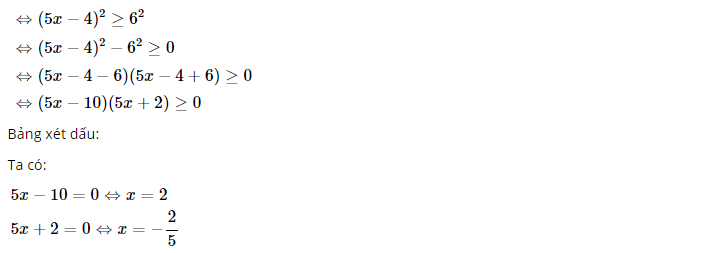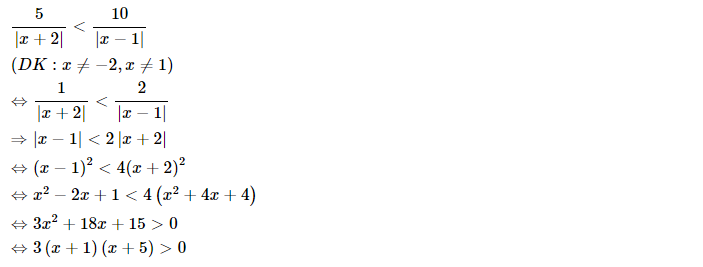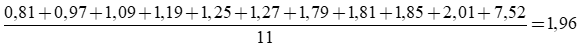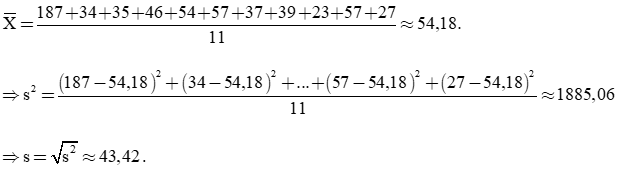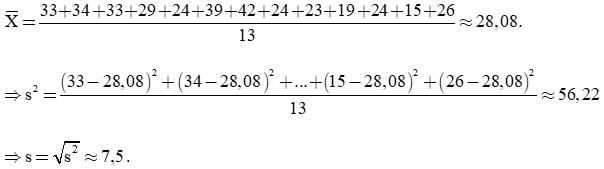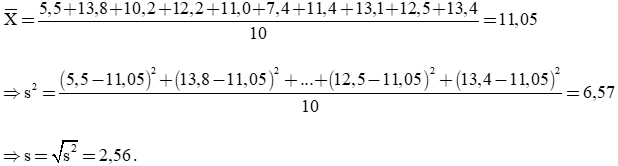Nhị thức là gì? Nhị thức bậc nhất là gì? Lý thuyết và bài tập?

1. Nhị thức là gì? nhị thức bậc nhất là gì?

Nhị thức (hay còn gọi là hệ số nhị thức) là một khái niệm trong toán học, dùng để tính số cách sắp xếp hoặc chọn một số phần tử trong một tập hợp. Ký hiệu của nhị thức là “nCk” hoặc “C(n, k)”, trong đó “n” và “k” là các số nguyên dương và “n” lớn hơn hoặc bằng “k”.

Nhị thức được tính theo công thức sau:

C(n, k) = n! / (k! * (n – k)!)

Trong đó, “n!” đại diện cho giai thừa của “n”, tức là tích của tất cả các số nguyên dương từ 1 đến “n”.

Một nhị thức bậc nhất là nhị thức khi “k” bằng 1, nghĩa là chỉ chọn một phần tử từ tập ban đầu. Công thức nhị thức bậc nhất là:

C(n, 1) = n! / (1! * (n – 1)!) = n

Nhị thức bậc nhất chỉ đơn giản là số phần tử trong tập hợp ban đầu.

2. Lý thuyết về nhị thức bậc nhất:

Định lý nhị thức bậc nhất

Ta có biểu thức f(x) = ax + b trong đó a, b là các số thực cho trước với điều kiện a # 0. Biểu thức trên là một nhị thức bậc nhất với ẩn x.

Định lý cơ bản về dấu của nhị thức bậc nhất

Cho nhị thức f(x) = ax + b (a #0).

• Dấu của nhị thức cùng dấu với hệ số a khi x nhận giá trị trong khoảng (-b/a; +∞).
• Dấu của nhị thức ngược dấu với hệ số a khi giá trị của x nằm trong khoảng (- ∞; -b/a).

Ta có bảng dấu của các nhị thức như sau:

Cách xét dấu hoặc thương của biểu thức nhị thức bậc nhất

Cho F(x) là tích của các nhị thức bậc nhất. Áp dụng định lý dấu cho các nhị thức bậc nhất ta xét được dấu của từng thừa số. Lập bảng dấu chung cho mọi nhị thức F(x) Ta tìm được dấu của F(x). Trường hợp F(x) là thương cũng được thực hiện tương tự.

Vận dụng lý thuyết đã sửa để giải các bất phương trình

Khi giải bài toán 10 dấu của nhị thức bậc nhất đối với bất phương trình f(x) > 0 ta xét dấu của biểu thức f(x) để biết khi nào biểu thức nhận giá trị dương, khi nào biểu thức nhận giá trị âm .

a) Giải các bất phương trình chứa ẩn ở mẫu

Làm thế nào để giải quyết vấn đề:

• Xác định điều kiện (Điều kiện) của bất phương trình.
• mẫu số đã cho
• Xét dấu của nhị thức và rút ra kết luận về tập nghiệm.

b) Giải bất phương trình chứa dấu tuyệt đối

Áp dụng tính chất của giá trị tuyệt đối, ta dễ dàng giải được các bài toán bất phương trình dạng |f(x)| ≤ a và |f(x)| ≥ a với điều kiện a > 0.

Ta có > 0:

Nếu |f(x)| ≤ a thì -a ≤ f(x) ≤ a

Nếu |f(x)| ≥ a thì f(x) -a hoặc giá trị f(x) ≥ a

3. Bài tập về nhị thức bậc nhất:

3.1. Bài tập 1 – Bài tập về nhị thức bậc nhất:

a) Từ biểu thức f(x) = (2x -1)(x +3) ta có hệ phương trình sau:

2x – 1 = 0 (1) và x + 3 = 0 (2). Giải (1) và (2) ta được:

x_{Đầu tiên} = ½

x₂ = -3

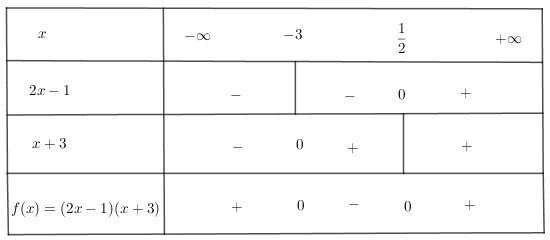
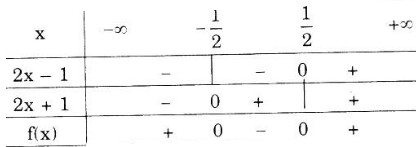
Ta có bảng dấu nhị thức sau:

Từ bảng trên, ta kết luận:

f(x) < 0 khi -3 < x < ½

f(x) = 0 nếu x = -3 hoặc x =

f(x) > 0 nếu x < -3 or x >

b) f(x) = (-3x -3)(x + 2)(x + 3)

Ta được hệ phương trình sau:

-3x – 3 = 0 (1)

x + 2 = 0 (2)

x + 3 = 0 (3)

Giải (1), (2) và (3) ta được các nghiệm sau: x_{Đầu tiên} = -1; x₂ = -2; x₃ = -3

Ta có bảng dấu nhị thức sau:

Vì vậy, chúng ta có thể kết luận:

f(x) < 0 khi x ∈ (-3; -2) ∪ (-1; + )

f(x) = 0 khi x = -3; x = -2 hoặc x = -1

f(x) > 0 khi x ∈ (- ; -3) ∪ ( -2; -1)

c) Biểu thức

Ta có bảng dấu nhị thức sau:

Từ bảng trên, ta kết luận:

d) Ta có: 4x² -1 = 0 (2x -1)(2x +1) = 0

Ta được hệ phương trình:

2x – 1 = 0 (1)

2x + 1 = 0 (2)

Giải (1) và (2) ta được x_{Đầu tiên} = ; x₂ = -½

Ta có bảng dấu nhị thức sau:

Từ bảng trên, chúng ta có thể kết luận:

f(x) < 0 khi x ∈ (-½ ; )

f(x) > 0 khi x ∈ ( -∞; -½ ) ∪ ( ½ ; +∞)

f(x) = 0 khi x = ±

Bài 2: SGK – 94

a) Ta có:

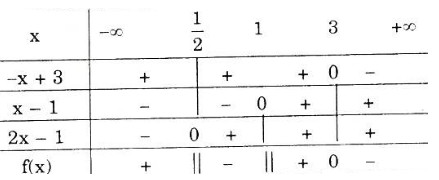
Ta có bảng dấu nhị thức sau:

Vậy phương trình đã cho có tập nghiệm S = (½ ; 1) [3; +∞)

b) Ta có:

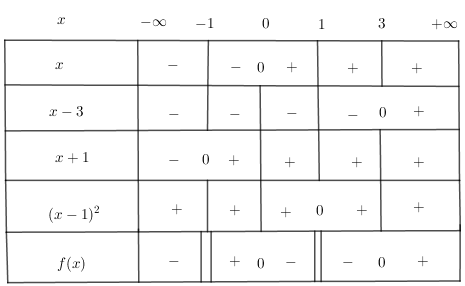
Ta có bảng xét dấu của nhị thức sau:

Vậy S = (-∞; -1) ∪ (0; 1) ∪ (1; 3) là nghiệm của phương trình trên.

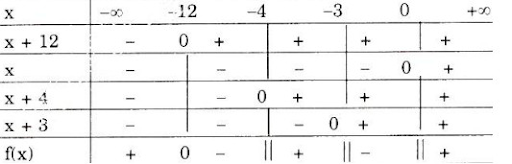
c) Ta có:

Có:

x = 0

x + 12 = 0 ⇔ x = -12

x + 4 = 0 ⇔ x = -4

x + 3 = 0 ⇔ x = -3

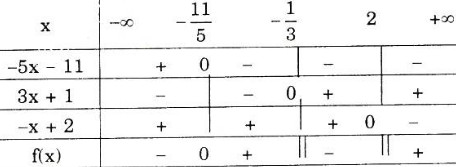
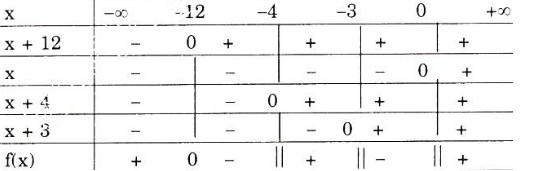
Ta có bảng xét dấu nhị thức:

Vậy S = (-12; -4) ∪ (-3; 0) là nghiệm của phương trình trên.

d) Ta có:

Ta có bảng xét dấu của nhị thức trên:

Ta có S= (-1; ⅔ ) ∪ ( 1; + ∞) là nghiệm của phương trình trên.

Bài 3: SGK – 94

a) Bình phương 2 vế ta được:

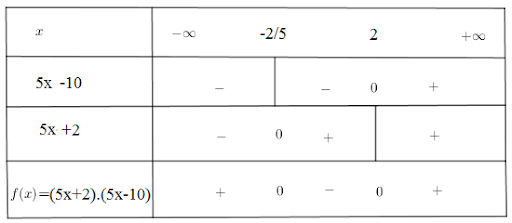
Ta có bảng xét dấu nhị thức:

Vậy S = ( –∞; -⅖ ] ∪[2;+∞)lànghiệmcủaphươngtrình[2;+∞)lànghiệmcủaphươngtrìnhđãcho[2;+∞)isthesolutionofthegivenequation[2;+∞)lànghiệmcủaphươngtrìnhđãcho

b) Ta có:

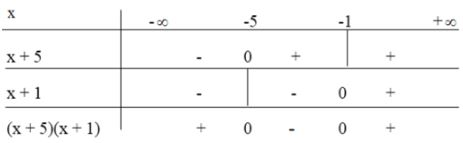
Bảng dấu của nhị thức:

Từ bảng các dấu hiệu, chúng tôi nhận được: x < -5 and x > -1

Kết hợp các điều kiện x # -2 và x # 1 ta thấy S = ( -∞; -5) ∪ (-1; 1) ∪ (1; +∞) là tập nghiệm của phương trình trên.

3.2. Bài tập 2 – Bài tập về nhị thức bậc nhất:

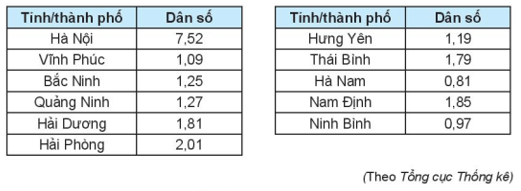
Bảng dưới đây thể hiện dân số các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (tính bằng triệu người).

a) Tìm giá trị trung bình và trung vị của mẫu số liệu trên.

b) Giải thích tại sao số trung bình và số trung vị lại khác nhau như vậy.

c) Giá trị trung bình hay số trung vị phải đại diện cho dân số các tỉnh đồng bằng Bắc Bộ?

Câu trả lời:

Sắp xếp dãy số liệu trên theo thứ tự không giảm, ta được:

0,81; 0,97; 1,09; 1,19; 1,25; 1,27; 1,79, 1,81; 1,85; 2,01; 7.52.

Trung bình cộng của chuỗi số liệu trên là:

Vì n = 11 là số lẻ nên trung vị là số ở giữa: Q₂ = 1,27.

b) Trong dữ liệu có giá trị ngoại lệ 7,52 ảnh hưởng đến giá trị trung bình của dữ liệu. Điều này dẫn đến sự khác biệt giữa giá trị trung bình và trung bình.

c) Trung bình và trung vị là các thuật ngữ thống kê có vai trò hơi giống nhau trong việc hiểu xu hướng trung tâm của tập hợp thống kê. Nhưng có giá trị 7,52 là một giá trị khác với phần còn lại, vì vậy nó ảnh hưởng đến mức trung bình. Vì vậy, chúng ta nên lấy trung vị là đại diện cho dân số của các tỉnh đồng bằng Bắc Bộ.

Bài 5.25 trang 90 Toán 10 Tập 1: Hai mẫu số liệu sau cho biết số trường trung học phổ thông của mỗi tỉnh ở đồng bằng Bắc Bộ?

Đồng bằng sông Hồng: 187 34 35 46 54 57 37 39 23 57 27.

ĐBSCL: 33 34 33 29 24 39 42 24 23 19 24 15 26.

a) Tính giá trị trung bình, trung vị, tứ phân vị, chế độ, phạm vi, phạm vi liên tứ phân vị và độ lệch chuẩn cho từng mẫu dữ liệu trên.

b) Tại sao giá trị trung bình của hai mẫu dữ liệu khác nhau rất nhiều trong khi trung vị thì không?

c) Tại sao khoảng và độ lệch chuẩn của hai mẫu dữ liệu khác nhau rất nhiều trong khi khoảng tứ phân vị thì không?

Câu trả lời:

a) +) Dữ liệu mẫu của Đồng bằng sông Hồng:

Giá trị trung bình của mẫu dữ liệu:

Sắp xếp các dữ liệu trên theo thứ tự không giảm, ta được:

23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.

Vì n = 11 là số lẻ nên trung vị là Q₂ = 39.

Nửa bên trái có tứ phân vị đầu tiên: Q_{Đầu tiên} = 34.

Nửa bên phải có phần tư thứ ba: Q₃ = 57.

Khoảng tứ phân vị là:

Δ_Hỏi = Q₃ – Hỏi_{Đầu tiên} = 57 – 34 = 23.

Ta có giá trị lớn nhất của dữ liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng dao động là: R = 187 – 23 = 164.

Theo quan sát dữ liệu ta thấy giá trị 57 có tần suất xuất hiện nhiều nhất nên mode là 57.

+) Dữ liệu mẫu của Đồng bằng sông Cửu Long:

Giá trị trung bình của mẫu dữ liệu:

Sắp xếp các dữ liệu trên theo thứ tự không giảm, ta được:

15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.

Vì n = 13 là số lẻ nên trung vị Q₂ = 26.

Nửa bên trái có tứ phân vị đầu tiên: Q_{Đầu tiên} = (23 + 24) : 2 = 23,5.

Nửa bên phải có phần tư thứ ba: Q₃ = (33 + 34):2 = 33,5.

Khoảng tứ phân vị là:

Δ_Hỏi = Q₃ – Hỏi_{Đầu tiên} = 33,5 – 23,5 = 10.

Ta có giá trị lớn nhất của dữ liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng dao động là: R = 42 – 15 = 27.

Theo quan sát dữ liệu ta thấy giá trị 24 có tần suất xuất hiện nhiều nhất nên mode là 24.

b) Do ở mẫu số liệu thứ nhất có giá trị ngoại lệ là 187 ảnh hưởng đến số trung bình cộng của mẫu số liệu thứ nhất nên giữa hai số trung bình của hai mẫu số liệu còn lại có sự chênh lệch lớn. hương vị không.

c) Do trong mẫu số liệu thứ nhất có giá trị ngoại lệ là 187, là giá trị lớn nhất ảnh hưởng đến biên độ dao động của mẫu số liệu thứ nhất. Trong khi đó, các giá trị của mẫu dữ liệu hai không có ngoại lệ. Do đó, biên độ dao động của hai mẫu dữ liệu là khác nhau.

Độ phân tán của dữ liệu mẫu một lớn hơn nhiều so với mẫu hai. Do đó, độ lệch chuẩn của hai dữ liệu sau là khác nhau.

Khoảng tứ phân vị là khoảng biến thiên nằm ở giữa 50% dữ liệu mà giá trị trung vị của hai mẫu không quá chênh lệch. Do đó, khoảng tứ phân vị của hai mẫu không quá chênh lệch.

3.3. Bài tập 3 – Bài tập về nhị thức bậc nhất:

Bài tập: Tỷ lệ trẻ em suy dinh dưỡng (tính theo cân nặng theo tuổi) của 10 tỉnh vùng đồng bằng sông Hồng như sau:

5,5 13,8 10,2 12,2 11,0 7,4 11,4 13,1 12,5 13,4.

a) Tính giá trị trung bình, trung vị, khoảng và độ lệch chuẩn của mẫu dữ liệu trên.

b) Thực hiện làm tròn đến hàng đơn vị cho tất cả các giá trị trong mẫu dữ liệu. Sai số tuyệt đối của phép làm tròn này không vượt quá bao nhiêu?

Câu trả lời:

a) Giá trị trung bình của mẫu dữ liệu là:

Sắp xếp dãy số liệu theo thứ tự không giảm, ta được:

5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13.8.

Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị ở giữa:

(11,4 + 12,2) : 2 = 11,8.

Ta có giá trị lớn nhất của dữ liệu là 13,8 và giá trị nhỏ nhất là 5,5. Khi đó biên độ dao động là: R = 13,8 – 5,5 = 8,3.

b) Thực hiện làm tròn đến hàng đơn vị cho các giá trị trong mẫu dữ liệu, ta được:

5,5; 7,4; 10,2; 11,0; 11,4; 12,2; 12,5; 13,1; 13,4; 13.8.

6 ; 7; mười; 11; 11; thứ mười hai; 13; 13; 13; 14.

Sai số của phép làm tròn này không vượt quá

Một	$\overline{\mathrm{Một}}$	$\left|\mathrm{Một}–\overline{\mathrm{Một}}\right|$
6	5,5	0,5
7	7.4	0,4
mười	10.2	0,2
11	11,0	0
11	11.4	0,4
thứ mười hai	12.2	0,2
13	12,5	0,5
13	13.1	0,1
13	13.4	0,4
14	13,8	0,2

Sai số tuyệt đối của phép làm tròn này không vượt quá 0,5.