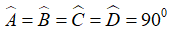Hình chữ nhật là gì? Tính chất, dấu hiệu nhận biết hình chữ nhật?

Bạn đang xem: Hình chữ nhật là gì? Tính chất, dấu hiệu nhận biết hình chữ nhật? tại truongptdtntthptdienbiendong.edu.vn

Hình chữ nhật là gì? Nhận biết hình chữ nhật? Các tính chất của một hình chữ nhật là gì? Ví dụ về hình chữ nhật? Bài tập ứng dụng?

1. Thế nào là hình chữ nhật?

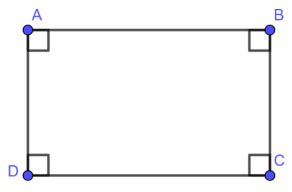
Định nghĩa: Hình chữ nhật là hình học quen thuộc, chúng ta dễ dàng bắt gặp những đồ vật có dạng hình chữ nhật. Hình chữ nhật là một tứ giác đặc biệt có bốn góc vuông.

Hình chữ nhật là gì? Định Nghĩa, Tính Chất Của Chi Tiết Hình Chữ Nhật

Tứ giác ABCD là hình chữ nhật Hình chữ nhật là gì? Định Nghĩa, Tính Chất Của Chi Tiết Hình Chữ Nhật

2. Nhận dạng hình chữ nhật:

Tứ giác có ba góc vuông là hình chữ nhật. Vì tổng các góc của một tứ giác bằng 180 độ nên khi một tứ giác có 3 góc vuông ta dễ dàng suy ra góc còn lại cũng bằng 90 độ. Vì tứ giác có 4 góc 90 độ nên ta có thể kết luận đó là hình chữ nhật.

Hình thang cân có một góc vuông là hình chữ nhật. Điều này chúng ta cũng có thể dễ dàng suy ra từ tính chất của hình thang cân.

Hình bình hành có một góc vuông là hình chữ nhật.

Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

3. Tính chất của hình chữ nhật:

Hình chữ nhật có tất cả các tính chất của hình bình hành và hình thang cân

Trong một hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường chéo. Hình chữ nhật có các cạnh đối song song và bằng nhau.

4. Ví dụ về hình chữ nhật:

Ví dụ 1: Tìm độ dài đường trung tuyến cạnh huyền của một tam giác vuông có các cạnh là 7 cm và 24 cm.

Câu trả lời gợi ý:

Gọi a là độ dài cạnh huyền của tam giác vuông.

Theo định lý Pitago ta có:

Một² = 7² + 24² = 625

một = 25cm

⇒ Độ dài đường trung tuyến đến cạnh huyền bằng: $frac{a}{2}$ = $frac{25}{2}$ = 12,5 (cm).

Ví dụ 2:

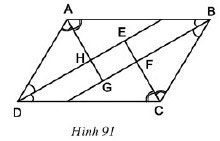
Cho ABCD là hình bình hành. Các tia phân giác của các góc A, B, C, D cắt nhau như hình 91. Chứng minh EFGH là hình chữ nhật.

bài học 64

Câu trả lời gợi ý:

Giả sử ABCD là hình bình hành, AD//BC, AB//CD

Bởi vì $AD//BC Mũi tên phải mũ rộng {DAB} + mũ rộng {ABC}= {180^0}$ (hai góc trong cùng phía phụ nhau)

Vì AG là tia phân giác $mũ rộng {DAB}$ (giả thiết)

$Rightarrow widehat {BAG}=widehat {DAH} = dfrac{1}{2}widehat {DAB}$ (tính chất của tia phân giác)

Vì BG là tia phân giác $mũ rộng {ABC}$ (giả thiết)

$Rightarrow widehat {ABG} = dfrac{1}{2}widehat {ABC}$

Vì thế: $widehat {BAG} + widehat {ABG} = dfrac{1}{2}left( {widehat {DAB} + widehat {ABC}} right) = dfrac{1}{2}{.180^0} = {90^ 0}$

Coi như $đồng bằng AGB$ Có:

$mũ rộng {BAG} + mũ rộng {ABG} = {90^0}$

Áp dụng định lý tổng ba góc trong một tam giác vào tam giác AGB, ta có:

$mũ rộng {BAG} + mũ rộng {ABG} + mũ rộng {AGB} = {180^0}$

$Rightarrowwidehat {AGB} =180^0- (widehat {BAG} + widehat {ABG} )=180^0-{90^0}=90^0$

$+ Vì$ AB//DC Mũi tên phải mũ rộng {DAB} + mũ rộng {ADC}= {180^0}

(hai góc trong cùng phía phụ nhau) $Vì DE là tia phân giác$ mũ rộng {ADC}

$(giả thiết)$ Rightarrow widehat {ADH}=widehat {EDC} = dfrac{1}{2}widehat {ADC}

(tính chất của tia phân giác) $Vì thế:$

widehat {DAH} + widehat {ADH} = dfrac{1}{2}left( {widehat {DAB} + widehat {ADC}} phải) = dfrac{1}{2}{.180^0} = {90^ 0}

$Áp dụng định lý tổng ba góc trong một tam giác vào tam giác ADH ta có:$

$mũ rộng {DAH} + mũ rộng {ADH} + mũ rộng {AHD} = {180^0}$

Rightarrowwidehat {AHD} =180^0- (widehat {DAH} + widehat {ADH} )=180^0-{90^0}=90^0 $tôi đoán$ AHbot HD $nên$

mũ rộng {EHG}=90^0 (**)

Chứng minh tương tự: $Chúng ta có:$ mũ rộng {DCB} + mũ rộng {ADC}= {180^0}

(hai góc trong cùng phía phụ nhau) $Nhưng$ widehat{ECD}=dfrac{1}2widehat {DCB}

(do CE là tia phân giác của góc DCB) $Nên$

widehat {EDC} + widehat {ECD} = dfrac{1}{2}left( {widehat {ADC} + widehat {DCB}} right) = dfrac{1}{2}{.180^0} = {90^ 0}

$Lại có:$ mũ rộng {EDC} + mũ rộng {ECD} + mũ rộng {DEC} = {180^0}

$(tổng ba góc trong tam giác DEC)$

Rightarrowwidehat {DEC} =180^0- (widehat {EDC} + widehat {ECD} )=180^0-{90^0}=90^0 $cỏ khô$

mũ rộng {HEF} = {90^0} (***)

Từ

(**) và (***) ta thấy tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

5. Bài tập áp dụng: A. Câu đố

Bài 1:

Chọn câu trả lời đúng nhất trong các phương án sau?

A. Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.

B. Hình chữ nhật là tứ giác có bốn góc vuông.

C. Hình chữ nhật là tứ giác có hai góc vuông. D. Các phương án trên đều không đúng.

Bài 2:

Tìm lỗi sai trong các câu sau

A. Trong hình chữ nhật có hai đường chéo bằng nhau.

B. Trong một hình chữ nhật, hai đường chéo cắt nhau tại trung điểm của mỗi đường chéo.

C. Trong hình chữ nhật, hai cạnh kề bằng nhau. D. Trong hình chữ nhật, giao điểm của hai đường chéo là tâm hình chữ nhật

Bài 3:

Dấu hiệu nào sau đây không đúng?

A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.

B. Tứ giác có ba góc vuông là hình chữ nhật.

C. Hình thang cân có một góc vuông là hình chữ nhật. D. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Bài 4:

Khoanh tròn câu trả lời sai

A. Trong một tam giác vuông, đường trung tuyến bằng cạnh huyền và bằng nửa cạnh huyền.

B. Trong một tam giác, đường trung tuyến bằng một cạnh và bằng nửa cạnh thì tam giác đó là tam giác vuông.

C. Trong một tam giác vuông, đường trung bình của cạnh góc vuông không bằng cạnh đó. D. Trong một tam giác vuông, đường trung tuyến của cạnh huyền vuông góc với cạnh huyền.

Bài 5:

Hình chữ nhật có các kích thước lần lượt là 5 cm và 12 cm. Độ dài đường chéo của hình chữ nhật là bao nhiêu?

MỘT.17 cm

B. 13cm

C. 119cm

D. 12cm

B. Tự luận

Bài 1:

Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh MNPQ là hình bình hành.

Tứ giác ABCD cần điều kiện gì thì MNPQ là hình chữ nhật.

Bài 2:

Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo (không vuông góc), I, K lần lượt là trung điểm của BC, CD. Gọi M, N lần lượt là điểm đối xứng của điểm O qua các tâm I, K.

a) Chứng minh tứ giác BMND là hình bình hành.

b) Hai đường chéo AC và BD với điều kiện gì thì tứ giác BMND là hình chữ nhật.

c) Chứng minh 3 điểm M, C, N thẳng hàng.

Bài 3:

Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của điểm M qua B. Gọi Q là điểm đối xứng của điểm N qua G.

a/ Tứ giác MNPQ là hình gì? Tại sao?

b/ Nếu ABC cân tại A thì tứ giác MNPQ là hình gì? Tại sao?

bài 4

Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của điểm M qua B. Gọi Q là điểm đối xứng của điểm N qua G.

a) Tứ giác MNPQ là hình gì? Tại sao? b) Nếu ABC cân tại A thì tứ giác MNPQ là hình gì? Tại sao?

Bài 5.

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G, K.

a) Chứng minh tứ giác AHCE là hình chữ nhật. b) Chứng minh HG = GK = KE.

Bài 6. Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì?

Bài 7.

Cho tam giác ABC vuông tại A. Về phía ngoài của tam giác ABC, vẽ hai tam giác vuông ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:

a) Ba điểm D, A, E thẳng hàng.

b) Tứ giác IAKM là hình chữ nhật. c) Tam giác DME là tam giác vuông cân.

Bài 8.

Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AD, BD, AC, BC.

a) Chứng minh bốn điểm M, N, P, Q thẳng hàng.

b) Chứng minh tứ giác ABPN là hình thang cân. c) Tìm hệ thức giữa AB và CD để ABPN là hình chữ nhật.

a) Chứng minh các tứ giác MNFD và MEFP là hình chữ nhật. b) Để các đoạn thẳng MD, ME và DP bằng nhau thì ABC phải là tam giác gì?