một vòng tròn là gì? Các tính chất của một vòng tròn là gì? một vòng tròn là gì? Cung và dây của một vòng tròn? Tính chất quan trọng của đường tròn – liên quan đến góc? Công Thức Hình Tròn Quan Trọng: Diện Tích Và Chu Vi? Áp dụng các tính chất trong câu hỏi?
1. Hình tròn là gì?
Đường tròn tâm O bán kính R là hình gồm tập hợp các điểm cách tâm O một khoảng bằng bán kính R. Điểm nào nằm trên đường tròn này và có đường nối nó với tâm O gọi là nửa -vòng tròn. kính.
(Trong đó: Điểm cố định trong đường tròn gọi là tâm; Bán kính là khoảng cách cố định giữa tâm và tập hợp các điểm. Kí hiệu là “R”)
Vị trí tương đối của một điểm bất kỳ với đường tròn tâm O, bán kính R
Ta nhận thấy có 3 vị trí tương đối giữa một điểm chẳng hạn A và đường tròn tâm O bán kính R bao gồm:
– Nếu điểm A nằm trong đường tròn (O,R) => OA < R
– Nếu điểm A nằm trên đường tròn (O,R) => OA = R
– Nếu điểm A nằm ngoài đường tròn (O,R) => OA < R
2. Tính chất của đường tròn:
Các đường tròn có chu vi bằng nhau thì bằng nhau.
Đường kính là đoạn thẳng dài nhất trong một vòng tròn:
– Đường kính là đoạn thẳng có các điểm biên là các đường tròn làm điểm cuối và đi qua tâm.
Vì vậy, về mặt logic, đường kính có thể được chia thành hai phần:
– Phần từ một điểm biên của đường tròn đến tâm
– Và, một phần khác từ trung tâm đến một điểm biên khác.
– Do đó, Đường kính = Hai lần chiều dài của bán kính hoặc “D = 2R”
Bán kính của các đường tròn bằng nhau sẽ bằng nhau.
Chu vi của hai hình tròn khác nhau sẽ tỉ lệ thuận với bán kính tương ứng của mỗi hình tròn.
Góc nằm ngang ở tâm của hình tròn là 360 độ.
Hai tiếp tuyến bất kỳ vẽ trên cùng một đường tròn từ một điểm bất kỳ ở ngoài sẽ có cùng độ dài.
Mọi tiếp tuyến của đường tròn đều vuông góc với bán kính tại tiếp điểm.
Hình tròn là hình có tâm và trục đối xứng với nhau.
3. Hình tròn là gì?
Đường tròn là tập hợp các điểm nằm trên đường tròn và nằm bên trong đường tròn đó.
4. Cung và dây hình tròn:
4.1. Cây cung:
Cung của hình tròn là một phần của chu vi. Chu vi là độ dài của hình tròn
Từ hai điểm bất kỳ nằm trên đường tròn vẽ được hai cung: cung nhỏ và cung lớn.
– Nơ nhỏ: Cung ngắn hơn được hình thành bởi hai điểm.
– Chính điện: Vòng cung dài hơn được tạo thành từ hai điểm.
Nếu hai điểm B và C bất kì nằm trên cùng một đường tròn (không trùng nhau) và đã chia đường tròn thành 2 phần thì mỗi phần là một cung. Hai điểm B và C gọi là hai điểm cuối của hai cung.
Nhìn vào hình dưới đây, chúng ta có thể thấy đâu là cung lớn và cung nhỏ.

4.2. Dây điện:
Đoạn thẳng nối hai điểm cuối B và C trong cung như hình vẽ trên gọi là dây cung. Nếu hai điểm cuối B và C đi qua tâm của đường tròn thì gọi là đường kính. Trong hình trên đường kính là đoạn thẳng AB.
4.3. Mối quan hệ giữa cung và dây:
Định lý 1:
Nếu 2 cung nhỏ của cùng một đường tròn hoặc 2 đường tròn bằng nhau thì:
- Nếu hai cung bằng nhau thì hai dây cung bằng nhau.
- Nếu hai dây bằng nhau thì các cung bằng nhau.
Định lý 2:
Nếu 2 cung nhỏ của cùng một đường tròn hoặc 2 đường tròn bằng nhau thì:
– Cung càng to thì dây càng to.
– Càng nhiều thì nguồn cung càng lớn.
Bên cạnh đó:
– Trong một đường tròn, đường kính AB đi qua trung điểm của một cung nào thì vuông góc với dây căng qua cung đó và chiều ngược lại cũng đúng.
– Đường kính AB đi qua trung điểm của một sợi dây bất kỳ và không đi qua tâm của đường tròn sẽ đi qua trung điểm của dây cung đã căng sẵn của sợi dây đó.
– Đường kính AB đi qua trung điểm của một cung bất kỳ thì cũng đi qua trung điểm của đoạn dây đã căng sẵn cung đó.
– Hai dây bị chặn giữa hai dây song song bất kỳ sẽ bằng nhau.
Đường tiếp tuyến:
Tiếp tuyến là tiếp tuyến của đường tròn tại một điểm bất kỳ.
Tính chất tiếp tuyến: Bán kính luôn vuông góc với tiếp tuyến tại điểm tiếp tuyến của đường tròn.
5. Tính chất quan trọng của đường tròn – liên quan đến góc:
góc nội tiếp
Góc nội tiếp là góc tạo thành giữa hai dây cung khi chúng cắt nhau trên một đường tròn.
Tính chất của góc nội tiếp
Đầu tiên Các góc tạo bởi cùng một cung trên một đường tròn luôn bằng nhau
2. Góc trong hình bán nguyệt luôn bằng 90°.
Góc trung tâm:
Góc ở tâm là góc được tạo thành khi hai đoạn thẳng cắt nhau sao cho một trong các điểm cuối của cả hai đoạn thẳng nằm ở tâm và điểm còn lại nằm ở ranh giới của đường tròn.
Tính chất của góc ở tâm
Góc tạo bởi cung ở tâm gấp đôi góc nội tiếp tạo bởi cung đó.
6. Công thức hình tròn quan trọng: Diện tích và chu vi:
Dưới đây là một số công thức toán học sẽ giúp bạn tính diện tích và chu vi/chu vi hình tròn.
Chu vi:
– Chu vi hoặc Chu vi hình tròn = 2 × π × R.
– Độ dài cung = (Góc ở tâm tạo bởi cung/360°) × 2 × π × R.
diện tích:
– Diện tích hình tròn = × R²
– Diện tích của diện tích =(Góc tâm tạo bởi diện tích/360°) × π × R².
Dưới đây là danh sách tóm tắt tất cả các thuộc tính mà chúng ta đã học được trong bài viết cho đến nay.
| thuộc tính quan trọng | ||
| Các dòng trong một vòng tròn | Dây nhau | Điểm rơi vuông góc từ tâm chia hợp âm thành hai phần bằng nhau. |
| Đường tiếp tuyến | Bán kính luôn vuông góc với tiếp tuyến tại điểm tiếp tuyến của đường tròn. | |
| Góc trong một vòng tròn | góc nội tiếp | 1. Các góc tạo bởi cùng một đường tròn thì luôn bằng nhau. 2. Góc trong nửa đường tròn luôn bằng 90. |
| góc trung tâm | Góc tạo bởi cung ở tâm gấp đôi góc nội tiếp tạo bởi cung đó. | |
| Công thức quan trọng | Chu vi của một vòng tròn | 2×π×R. |
| Chiều dài của một cung |
|
|
| khu vực vòng tròn | ×R | |
| Diện tích của một ngành công nghiệp | (Góc ở tâm tạo bởi cung/360°) × × R² | |
7. Áp dụng các tính chất trong câu hỏi:
câu hỏi 1
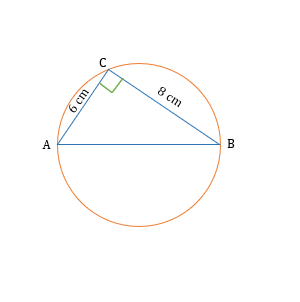
Độ dài hai cạnh góc vuông trong tam giác vuông khác cạnh huyền là 6 cm và 8 cm. Nếu tam giác vuông này nội tiếp trong một đường tròn thì diện tích hình tròn đó là bao nhiêu?
A. 5π
B. 10π
C. 15π
D. 20π
E. 25π
Giải pháp
Bước 1: Cho
Độ dài của hai cạnh khác cạnh huyền của một tam giác vuông là 6 cm và 8 cm.
Tam giác này được ghi trong một vòng tròn.
Bước 2: Để tìm
Khu vực hình tròn.
Bước 3: Tiếp cận và giải quyết
Hãy để chúng tôi vẽ biểu diễn sơ đồ.
Bằng cách áp dụng tính chất góc trong một hình bán nguyệt 90º, chúng ta có thể nói rằng AB là đường kính của hình tròn.
Và, một khi chúng ta tìm được độ dài của đường kính, chúng ta có thể tìm được bán kính, và sau đó chúng ta cũng có thể tìm được diện tích của hình tròn.
Áp dụng định lý Pythagoras trong △ ABC,
AB² = AC² + BC²
AB² = 6² + 8² = 36 +64 = 100
AB = 10 cm
Vì AB là đường kính nên AB = 2R = 10
Do đó, R = 5 cm.
Diện tích hình tròn = π × R²= π × 5² = 25 π.
Do đó, đáp án đúng là phương án E.
Câu hỏi 2
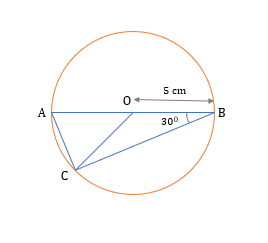
Trong sơ đồ trên, O là tâm của vòng tròn. Cho OB = 5 cm và ABC = 30 0 độ dài cung AC là bao nhiêu?
A. 5π/6
B. 5π/3
C. 5π/2
D. 5π
E. 10π
Giải pháp
Bước 1: Cho
– OB = 5 cm
– ABC = 30°
Bước 2: Để tìm
chiều dài cung
Bước 3: Tiếp cận và giải quyết
Độ dài cung = (Góc tâm tạo bởi cung/360°) × 2 × π × R.
Để tìm độ dài của cung, chúng ta cần giá trị của hai biến, góc ở tâm tạo bởi cung và bán kính.
– Ta đã cho bán kính OB = 5cm
– Tôi cần tìm AOC
Quan sát đồ thị, góc nội tiếp bởi cung AC là ∠ABC, góc có tâm bởi cung AC là ∠AOC.
– Do đó ta có thể áp dụng tính chất góc tạo bởi một dây cung bằng hai lần góc nội tiếp tạo bởi chính dây cung đó.
– Do đó, AOC = 2 × ∠ABC = 2 × 30° = 60°
Bây giờ, chúng ta cũng biết góc ở tâm tạo bởi cung.
- Do đó, độ dài cung AC =(Góc ở tâm tạo bởi cung/360°) × 2 × π × R.
- =(60°/360°) × 2 × π × 5.
- =(1/6) × 2 × π × 5.
- =(5π/3) cm
Như vậy, đáp án đúng là phương án B.