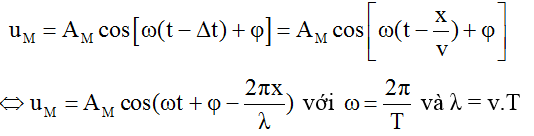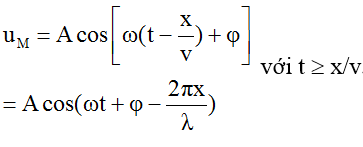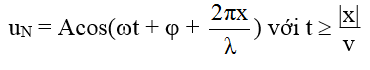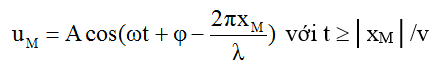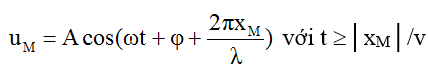Sóng là một
Bước sóng (Wavelength): Bước sóng là khoảng cách giữa hai điểm liên tiếp trên cùng một chu kỳ của sóng. Nó được ký hiệu bằng λ (lambda) và đo bằng mét (m) hoặc các đơn vị dài khác tùy vào quy mô của sóng. Bước sóng
Tần số (Frequency): Tần số là số lần dao động của sóng xảy ra trong một đơn vị thời gian. Đơn vị đo tần số thường được sử dụng là Hz (Hertz), tương đương với một dao động trong một giây. Tần số đảm bảo tính chất âm thanh và tần số của ánh sáng.
Biên độ (Amplitude): Biên độ của sóng là khoảng cách tối đa mà các phần tử dao động lên và xuống từ vị trí cân bằng trong quá trình dao động. Biên độ quyết định độ lớn của dao động.
Tốc độ lan truyền (Propagation Speed): Tốc độ lan truyền của sóng là tốc độ mà sóng di chuyển qua không gian. Nó liên quan đến bước sóng và tần số thông qua công thức v = λf.
Pha (Phase): Pha của sóng chỉ ra vị trí tương đối của một điểm trên sóng tại một thời điểm cụ thể. Nó được đo bằng radian hoặc độ. Pha quyết định vị trí và hình dạng của sóng tại một thời điểm nhất định.
Hướng dao động (Polarization): Hướng dao động chỉ ra hướng mà các phần tử dao động của sóng chuyển động. Có thể là ngang-trên, ngang-dưới (cho sóng ngang) hoặc lên-xuống, trái-phải (cho sóng dọc).
Cường độ (Intensity): Cường độ của sóng chỉ ra năng lượng truyền tải qua một đơn vị diện tích trong một đơn vị thời gian. Điều này thường liên quan đến độ sáng trong trường hợp ánh sáng.
Năng lượng (Energy): Năng lượng của sóng liên quan đến cường độ và thời gian tồn tại của sóng. Nó cũng liên quan mật thiết với tính chất của sóng và cách nó tương tác với các vật thể khác.
Độ pha (Phase Velocity): Độ pha của sóng là tốc độ mà một điểm trên sóng dao động qua một điểm cố định trong không gian. Độ pha liên quan chặt chẽ với tốc độ lan truyền.
Độ dài sóng biểu thị (Waveform Representation): Độ dài sóng biểu thị một cách diễn đạt các biến thiên của sóng theo thời gian. Điều này quan trọng trong việc biểu diễn sóng và phân tích sự biến đổi của nó.
Tóm lại, các đại lượng đặc trưng của sóng đóng vai trò quan trọng trong việc mô tả và hiểu hiện tượng sóng trong nhiều lĩnh vực khác nhau của vật lý và kỹ thuật. Chúng giúp chúng ta phân tích và ứng dụng sóng một cách hiệu quả, từ âm thanh, ánh sáng đến các loại sóng khác
5. Phường trình của sóng:
5.1. Phương trình sóng tại một điểm:
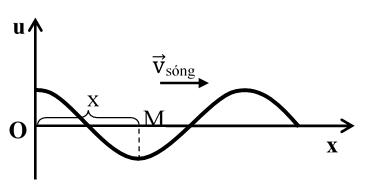
* Xét một sóng hình sin đang lan truyền trong một
Điểm M cách O một khoảng x. Sóng từ O truyền đến M mất khoảng thời gian ∆t = x/v.
Phương trình dao động của M là:
Nếu bỏ qua mất mát năng lượng trong quá trình truyền sóng thì biên độ sóng tại O và M bằng nhau: Ao = AM = A thì:
Chú ý: Phương trình sóng truyền theo chiều âm trục Ox đến điểm N có tọa độ x là:
5.2. Tổng quát:
Tại điểm O: uo = Acos( ωt + j) (ở đây O là gốc tọa độ nhưng không phải là nguồn sóng)
* Tại điểm M cách O một đoạn x trên phương truyền sóng.
+ Nếu sóng truyền theo chiều dương của trục Ox thì:
+ Sóng truyền theo chiều âm của trục Ox thì:
+ Tại một điểm M xác định trong môi trường sóng: x = const; uM là hàm điều hòa theo t với chu kỳ T.
+ Tại một thời điểm xác định t = const ; uM là hàm biến thiên điều hòa theo không gian x với chu kỳ λ.
Chú ý:
+ Tập hợp các điểm cùng khoảng cách đến nguồn sóng đều dao động cùng pha!
+ Nếu tại thời điểm t < |xM|/v thì li độ dao động điểm M luôn bằng 0 (uM = 0) vì sóng chưa truyền đến M.
5.3. Độ lệch pha 2 điểm M1, M2 do cùng 1 nguồn truyền đến:
Phương trình dao động tại nguồn là: u = a.cos(ωt + Φ).
– Phương trình dao động của nguồn truyền đến M1: u1M = a.cos(ωt + Φ – 2πd1/λ) với t ≥ d1/v
– Phương trình dao động của nguồn truyền đến M2: u2M = a.cos(ωt + Φ – 2πd2/λ) với t ≥ d2/v
– Độ lệch pha giữa M1 và M2 là: ΔΦ = 2π/λ.(d2 – d1)
– Để hai dao động cùng pha thì ΔΦ = 2kπ => (d2 – d1) = 2kπ => (d2 – d1) = k.λ
– Để hai dao động ngược thì ΔΦ = (2k+1)π
=> .(d2 – d1) = (2k + 1)π => (d2 – d1) = (k + 0,5)λ
Vậy khoảng cách giữa hai điểm trên phương truyền sóng lệch pha nhau góc ΔΦ (rad) là: L = ΔΦ/2π.λ
=> Trong hiện tượng truyền sóng, khoảng cách ngắn nhất trên phương truyền sóng giữa hai điểm dao động cùng phaa là 1λ, dao động ngược pha là λ/2, dao động vuông pha là λ/4 và dao động lệch pha nhau π/4 là λ/8.
Lưu ý:
+ Đơn vị của x, x1, x2, d, l và v phải tương ứng với nhau.
+ Trong hiện tượng truyền sóng trên sợi dây thép, dây được kích thích dao động bởi nam châm điện với tần số dòng điện là f thì tần số dao động của dây là 2f → fsóng = 2f.
6. Bài tập vận dụng:
Câu 1: Sóng dọc lan truyền trong một môi trường với bước sóng 15 cm với biên độ không đổi A = 5√3 cm . Gọi M và N là hai điểm cùng nằm trên một phương truyền sóng mà khi chưa có sóng truyền đến lần lượt cách nguồn các khoảng 20 cm và 30 cm. Khoảng cách xa nhất và gần nhất giữa 2 phần tử môi trường tại M và N khi có sóng truyền qua là bao nhiêu?
A. lmax = 11,5cm, lmin = 8,5cm B. lmax = 20cm, lmin = 0cm
C. lmax = 15cm, lmin = 5cm D. lmax = 14cm, lmin = 5cm
Lời giải:
Chọn A
Giả sử sóng truyền qua M rồi đến N thì dao động tại M sớm pha hơn dao động tại N: Δφ = 2πMN/λ = 4π/3
Chọn lại gốc thời gian để phương trình dao động tại M là: u1 = 5√3 cos ωt (mm) thì phương trình dao động tại N là u2 = 5√3 cos (ωt – 4π/3) mm .
Độ lệch li độ của hai phần tử tại M và tại N:
Δu = u2 – u1 = 5√3cos(ωt – 4π/3) – 5√3 cos(ωt) = 15 cos (ωt + 5π/6) cm
→ ∆umax = 15mm = 1,5cm < MN.
Vì đây là sóng dọc nên khoảng cách xa nhất và gần nhất giữa hai phần tử tại M và N:
Câu 2: Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, biên độ 4cm có tốc độ 12 m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 15cm. Nếu là sóng ngang thì hai phần tử môi trường tại A và B cách nhau đoạn lớn nhất là
A. 26cm. B. 15cm C. √257 cm D. 10√5 .
Lời giải:
Chọn C
Bước sóng: λ = v/f = 12/20 = 0,6m = 60cm.
Giả sử sóng truyền qua A rồi mới đến B thì dao động tại A sớm hơn dao động tại B: Δφ = 2πAB/λ = π/2
Độ lệch li độ của hai phần tử tại M và tại N:
Δu = uB – uA = 4cos(40πt) – 4cos(40πt + π/2) = 4√2 cos (20πt – π/4) cm
=> Δumax = 4√2 cm
Khoảng cách xa nhất giữa hai phần tử tại A và B: