1. Dao động điều hòa là gì?
1.1. Một số khái niệm liên quan:
Dao động cơ học là sự chuyển động của một vật quanh một vị trí xác định gọi là vị trí cân bằng, bao gồm 2 dạng phổ biến là Dao động tuần hoàn và Dao động điều hòa.
Một dao động cơ học của con lắc lò xo được biểu diễu theo hàm Sin hoặc Cos theo thời gian t như sau: x = A.cos ( ωt + Ψ ), v = – ωA.sin( ωt + Ψ ), a = -ω².cos ( ωt + Ψ )
Trong đó: x – Li độ ( cm hoặc m ), v – Vận tốc ( m / s hoặc cm / s ), a – Gia tốc ( cm / s² hoặc m / s² ), t – Thời gian ( s ), A – Biên độ ( cm ), ω – Tần số góc ( rad / s ), Ψ – Pha ban đầu ( rad )
Dao động tuần hoàn là dao động có tuần xuất lặp đi lặp lại sau một thời gian nhất định.
1.2. Khái niệm dao động điều hòa:
Dao động điều hòa là một loại dao động tuần hoàn đơn giản, có li độ (x) là hàm sin hoặc hàm cosin (hàm số lượng giác). Do đó, các đồ thị của dao động điều hòa thường được biểu diễn bằng đồ thị hàm số sin hoặc cosin.
Dao động điều hòa là trường hợp đơn giản nhất của dao động tuần hoàn.
2. Phương trình dao động điều hòa:
Tìm A:
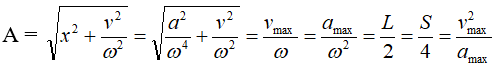
Trong đó:
– L là chiều dài quỹ đạo của dao động
– S là quãng đường vật đi được trong một chu kỳ
– Tìm ω:
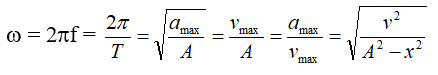
– Tìm φ
Cách 1: Dựa vào t = 0 ta có hệ sau:
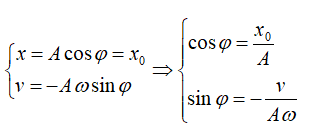
(Lưu ý: v.φ < 0)
Cách 2: Sử dụng vòng tròn lượng giác (VLG)
Góc Φ là góc hợp bởi giữa trục Ox và OM tại thời điểm ban đầu.
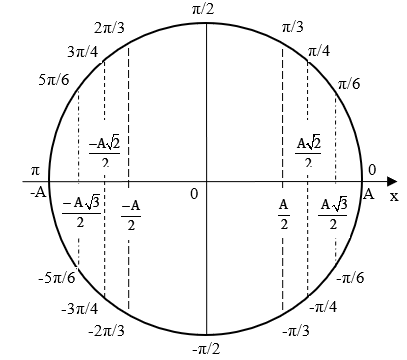
Cách 3: Thay kết quả vào phương trình: x = Acos(ωt + Φ ) được phương trình dao động điều hòa của vật.
Như vậy, ta có dao động điều hòa:
Phương trình x = Acos( ωt + φ) được gọi là phương trình dao động điều hòa
+ Với : A: biên độ dao động
ωt + φ (rad): pha dao động tại thời điểm t
φ(rad): pha ban đầu tại t = 0
Chú ý: Dao động điều hòa là hình chiếu của chuyển động tròn đều.
3. Chu kì, tần số, tần số góc của dao động điều hòa:
Chu kì T của dao động điều hòa là khoảng thời gian để thực hiện được một dao động toàn phần. Đơn vị: giây (s)
Tần số f của dao động điều hòa là số dao động toàn phần thực hiện được trong một giây. Đơn vị: héc (Hz)
Tần số góc ω là đại lượng liên hệ với chu kì T hay với tần số f qua hệ thức dưới đây:
ω=T2π=2πf
– Đơn vị của tần số góc là rad/s.
– Một chu kì dao động vật đi được quãng đường là S = 4A.
– Chiều dài quỹ đạo chuyển động của vật là L = 2A.
4. Vận tốc và gia tốc của dao động điều hòa:
– Vận tốc của dao động điều hòa có công thức:
– Gia tốc của dao động điều hòa:
a=v′=x′′=−ω2A=−ω2Acos(ωt+φ)=ω2Acos(ωt+φ+π)
Vecto gia tốc luôn có vị trí cân bằng
Gia tốc có độ lớn tỉ lệ với độ lớn của li độ
Tại biên, gia tốc có độ lớn cực đại
Tại VTCB, gia tốc có độ lớn bằng 0
Gia tốc nhanh pha hơn độ lớn một góc và ngược pha với số độ góc
5. Mối liên hệ dao động điều hòa và chuyển động tròn đều:
Dao động điều hòa có thể hiểu là hình chiếu của 1 chuyển động tròn đều xuống 1 trục nằm trong mặt phẳng quỹ đạo. Dựa vào hình chiếu này ta có thể dễ dàng xác định được trạng thái ban đầu và trạng thái dao động của vật. Để xác định đơn giản, ta thực hiện theo các bước sau:
- Bước 1: Vẽ đường tròn và hệ trục tọa độ với tâm nằm ở gốc tọa độ; bán kính bằng biên độ (A)
- Bước 2: Tại t = 0 xét vật bắt đầu ở đâu và chuyển động theo chiều âm hay dương.
- φ > 0: Chuyển động theo chiều âm (về biên âm)
- φ < 0: Chuyển động theo chiều dương (về biên dương)
- Bước 3: Xác định được điểm tới góc quét từ đó suy ra được quãng đường và thời gian chuyển động.
6. Bài tập vận dụng lý thuyết về dao động điều hòa:
Đây là dạng toán xác định đại lượng như biên độ A, vận tốc góc ω, chu kỳ, tần số, pha ban đầu từ một số dữ kiện cho trước … bằng cách đồng nhất với phương trình dao động điều hòa chuẩn.
– Dao động điều hòa được xem là một dao động mà li độ của vật được mô tả bằng hàm cosin hay sin theo biến thời gian. Một cách khác, một dao động điều hòa có phương trình là nghiệm của phương trình vi phân: x’’ + ω2x = 0 có dạng như sau:
x = Acos(ωt + φ)
Trong đó:
x: Li độ, li độ là khoảng cách từ vật đến vị trí cân bằng ( Đơn vị độ dài)
A: Biên độ (li độ cực đại) ( Đơn vị độ dài)
ω: Vận tốc góc (rad/s)
ωt + φ: Pha dao động (rad/s) tại thời điểm t, cho biết trạng thái dao động của vật ( gồm vị trí và chiều )
φ : Pha ban đầu (rad) tại thời điểm t = 0s, phụ thuộc vào cách chọn gốc thời gian, gốc tọa độ.
Chú ý: φ, A là những đại lượng hằng, lớn hơn 0.
– Phương trình vận tốc v (m/s)
v = x’ = ωAcos(ωt + φ + π/2)
Suy ra: vmax = ωA Tại vị trí cân bằng x = 0, vmin = 0 đạt được tại 2 biên.
Nhận xét: Xét 1 dao động điều hoà, ta có vận tốc sẽ sớm pha hơn li độ góc π/2.
– Phương trình gia tốc a (m/s2)
a = v’ = x’’ = a = – ω2x = ω2Acos(ωt + φ + π/2)
suy ra: amax = ω2A tại 2 biên, amin = 0 tại vtcb x = 0
Nhận xét: dựa vào các biểu thức trên, khi xét 1 dao động điều hòa ta có gia tốc ngược pha với li độ và sớm pha hơn vận tốc góc π/2
– Chu kỳ: T = 2/ω
Định nghĩa chu kì là thời gian để vật thực hiện được một dao động hoặc thời gian ngắn nhất để trạng thái dao động lặp lại như cũ.
– Tần số: f = ω/2 = 1/T
Bài tập 1:
Cho một vật dao động điều hòa với phương trình x = 5cos(4πt + π).Xác định chu kỳ, biên độ và vị trí tại thời điểm t = 0 ?
Hướng dẫn giải:
Dựa vào phương trình dao động điều hòa chuẩn, ta có:
A = 5, T = 2π/ω = 2π/4π = 1/2
Tại thời điểm t = 0, thế vào phương trình ta được: x = 5cos(π) = -5
Câu hỏi trắc nghiệm:
Dao động điều hòa là:
A. dao động được mô tả bằng định luật hàm sin hay hàm cos theo thời gian.
B. chuyển động tuần hoàn trong không gian, lặp đi lặp lại xung quanh một vị trí cố định.
C. dao động có năng lượng không đổi theo thời gian.
D. dao động được lặp đi lặp lại như cũ sau những khoảng thời gian xác định.
Đáp án đúng: A
Bài tập 2: (Bài 6 trang 8 Sách giáo khoa Vật lý 12) Một vật dao động điều hòa theo phương trình x = Acos(ωt + φ).
a) Lập công thức tính vận tốc và gia tốc của vật.
b) Ở vị trí nào thì vận tốc bằng 0? Ở vị trí nào thì gia tốc bằng 0?
c) Ở vị trí nào thì vận tốc có độ dài cực đại? Ở vị trí nào thì gia tốc có độ lớn cực đại?
Hướng dẫn giải:
a) Công thức vận tốc v = x’


