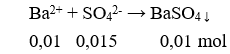1. Các trường hợp tam giác bằng nhau:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết : 
1.1. Trường hợp bằng nhau thứ nhất của tam giác (cạnh – cạnh – cạnh):
+ Xét ∆ABC và ∆DFE có:
AB = DF (gt)
AC = DE (gt)
BC = EF (gt)
Suy ra ∆ABC = ∆DFE (c – c – c)
(các cặp góc tương ứng)
2.2. Trường hợp bằng nhau thứ hai của tam giác (cạnh – góc – cạnh):
Định lý
Nếu góc xen giữa và hai cạnh của tam giác này bằng góc xen giữa và hai cạnh của tam giác kia thì hai tam giác đó bằng nhau.
+ Xét ∆ABC và ∆DFE có:
AB = DF (gt)
(gt)
AC = DE (gt)
Suy ra ∆ABC = ∆DFE (c – g – c)
(góc tương ứng) và BC = EF (cạnh tương ứng)
Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
Áp dụng cho tam giác vuông
Nếu hai cạnh của một tam giác vuông bằng lần lượt hai cạnh của một tam giác vuông khác, ta có thể kết luận rằng hai tam giác vuông đó là như nhau. Tương tự, nếu cạnh góc vuông và cạnh huyền của một tam giác tương ứng bằng với cạnh góc vuông và cạnh huyền của một tam giác khác, ta có thể kết luận rằng hai tam giác vuông đó là như nhau.
Dạng bài toán phổ biến
Dạng 1: Chứng minh sự tương đồng giữa hai tam giác dựa trên trường hợp cạnh – góc – cạnh.
Phương pháp giải:
Sử dụng định nghĩa: “nếu góc xen giữa và hai cạnh của một tam giác này bằng góc xen giữa và hai cạnh của một tam giác khác, thì hai tam giác đó là như nhau.” Hoặc sử dụng hệ quả: “nếu hai cạnh của một tam giác vuông bằng với hai cạnh lần lượt của tam giác vuông khác, thì hai tam giác vuông đó là như nhau.”
Dạng 2: Chứng minh sự bằng nhau của đoạn thẳng hoặc các góc. Tính độ dài của đoạn thẳng và số đo góc.
Phương pháp giải:
Chọn hai tam giác có các yếu tố cần chứng minh hoặc cần tính. Chứng minh sự tương đồng giữa hai tam giác theo trường hợp cạnh – góc – cạnh. Suy ra các thông tin cần thiết để giải quyết bài toán.
2.3. Trường hợp bằng nhau thứ ba của tam giác (góc – cạnh – góc):
Định lý
Nếu hai góc kề và một cạnh của một tam giác này bằng với hai góc kề và một cạnh của tam giác kia thì hai tam giác đó là tam giác bằng nhau.
+ Xét ∆ABC và ∆DFE có:
(gt)
AB = DF (gt)
Suy ra ∆ABC = ∆DFE (g – c – g)
(góc tương ứng) và AC = DE, BC = EF (cạnh tương ứng)
Chú ý:
- Hai cạnh bằng nhau phải tạo ra hai cặp góc bằng nhau để kết luận rằng hai tam giác đó là bằng nhau.
- Khi hai tam giác đã được chứng minh là bằng nhau, chúng ta có thể suy ra những yếu tố tương ứng còn lại là bằng nhau.
Áp dụng vào tam giác vuông
Hệ quả 1: Nếu một góc nhọn của một tam giác vuông trùng với một góc nhọn và một cạnh của tam giác vuông khác, thì hai tam giác vuông đó là bằng nhau.
Hệ quả 2: Nếu góc nhọn và cạnh huyền của một tam giác vuông tương ứng với góc nhọn và cạnh huyền của tam giác vuông khác, thì hai tam giác vuông đó là bằng nhau.
Dạng toán thường gặp tam giác bằng nhau
Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc.
Phương pháp giải:
Sử dụng trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông và góc – cạnh – góc của tam giác để chứng minh tam giác bằng nhau.
Dạng 2: Chứng minh 2 đoạn thẳng bằng nhau và tính độ dài của đoạn thẳng.
Phương pháp giải:
Chọn 2 tam giác có chứa đoạn thẳng cần tính. Chứng minh hai tam giác bằng nhau theo trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc. Suy ra các yếu tố cần để giải được bài toán.
Dạng 3: Sử dụng các trường hợp tam giác bằng nhau.
Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác như cạnh – góc – cạnh, cạnh – cạnh – cạnh, góc – cạnh – góc và một số trường hợp bằng nhau của tam giác vuông.
3. Bài tập về các trường hợp bằng nhau của tam giác:
a) Trường hợp 1: cạnh – cạnh – cạnh
Bài 1: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cách nhau giữa ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC
(hai góc tương ứng bằng nhau) mà hai góc ở vị trí so le trong Do đó AD // BCBài 2: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng mình rằng AM vuông góc với BC.
Gợi ý đáp án
b) Trường hợp 2: cạnh – góc – cạnh
Bài 1: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC
(vì AM ⊥ BC) AH là cạnh chung Nên ΔAMB = ΔAMC (c-g-c) ⇒ AB = AC (hai cạnh tương ứng)Bài 2: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.
a) Chứng mình rằng: ΔAOC = ΔBOD
b) Chứng minh O là trung điểm của CD
Gợi ý đáp án
a) Xét ∆AOC và ∆BOD có:
OA = OB (gt)
(gt)
AC = BD (gt)
Suy ra ∆AOC = ∆BOD (c – g – c)
b) Vì ∆AOC = ∆BOD (cmt)
Mà tia OC và OD là hai tia nằm khác phía đối với AB nên suy ra O, C, D thẳng hàng (hai tia đối của hai góc đối đỉnh hay O nằm giữa CD) Ta có: O nằm giữa C và D nên OC = OD hay O là trung điểm của CD
c) Trường hợp 3: góc – cạnh – góc:
Bài 1: Cho ΔABC có 
. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thằng BD và CE.
(gt) BC chung 
Suy ra ∆EBC = ∆DCB (g – c – g) Suy ra BD = CE (cặp cạnh tương ứng bằng nhau)B. Bài tập tự luyện
Câu 1: Phát biểu các trường hợp bằng nhau của tam giác? Vẽ hình minh họa cho mỗi trường hợp?
Câu 2: Phát biểu các trường hợp bằng nhau của tam giác vuông? Vẽ hình minh họa cho mỗi trường hợp?
Câu 3: Phát biểu định lí một đường thẳng vuông góc với mọt trong hai đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh họa?
Câu 4: Phát biểu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết kết luận? Vẽ hình minh họa?
Câu 5: Phát biểu định lí ba đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh?
Câu 6: Các em tự tìm hiểu những t/c, định lí nào có liêu quan đến các trường hợp bằng nhau của tam giác? Kể tên?
Sau khi nắm rõ các lý thuyết bên trên về những trường hợp bằng nhau của tam giác, mời các bạn cùng làm các bài tập ứng dụng dưới đây:
B. Bài tập tự luyện
Bài 1: Cho tam giác ABC; M là trung điểm BC; N là 1 điểm trong tam giác sao cho NB = NC.
Chứng minh: ∆NMB = ∆ NMC.
Bài 2. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ABE = ACE
Bài 3. Cho tam giác ABC có góc A = 400 , AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.
Bài 4. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a. Chứng minh góc EAB = góc DAC.
b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.
c. Giả sử góc DAE = 600. Tính các góc còn lại của tam giác DAE.
Bài 5. Cho tam giác ABC có góc A = 900. Vẽ AD ⊥ AB (D, C nằm khác phía đối với AB) và AD = AB. Vẽ AE ⊥ AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.
Bài 6. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:
a. ∆ABE = ∆ACE
b. AE là đường trung trực của đoạn thẳng BC.
Bài 7. Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a. ∆BDF = ∆EDC.
b. BF = EC.
c. F, D, E thẳng hàng.
d. AD ⊥ FC
Bài 8. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).
a. Chứng minh ∆OAD = ∆OBC
b. So sánh 2 góc CAD và CBD.
Bài 9. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a. Chứng minh ΔABC = ΔABD
b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.
Bài 10. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a. ΔAOI = ΔBOI.
b. AB ⊥ OI.
