Hình chữ nhật là một trong những kiến thức toán quan trọng đã được học trong chương trình học lớp 5. Tuy nhiên, không phải ai cũng nhớ nó. công thức tính thể tích hình hộp chữ nhật cách và cách tính thể tích hình hộp chữ nhật?
Tại đây, đội ĐẢO NGƯỢC chúng tôi sẽ hướng dẫn bạn cách tính thể tích hình hộp chữ nhật Đơn giản, chi tiết, dễ hiểu qua bài viết sau.
Mục lục bài viết [Ẩn]

Hình hộp chữ nhật là gì? Thể tích của hình hộp chữ nhật là bao nhiêu?
Hình hộp chữ nhật là hình không gian có 6 mặt đều là hình chữ nhật. Trong đó 2 mặt của hình hộp chữ nhật không có cạnh chung gọi là 2 mặt đối diện và được coi là 2 mặt đáy, các mặt còn lại được coi là mặt bên.
Thể tích hình hộp chữ nhật là khoảng không gian mà hình chiếm chỗ, được tính bằng tích của diện tích đáy và chiều cao.
Tính chất của hình hộp chữ nhật:
- Hình chữ nhật có 12 cạnh, 8 đỉnh, 6 mặt.
- Các đường chéo có 2 điểm cuối là 2 đỉnh đối diện của hình hộp chữ nhật đồng quy tại 1 điểm
- Diện tích hai mặt đối diện trong hình hộp chữ nhật bằng nhau
- Chu vi hai mặt đối diện trong hình hộp chữ nhật bằng nhau
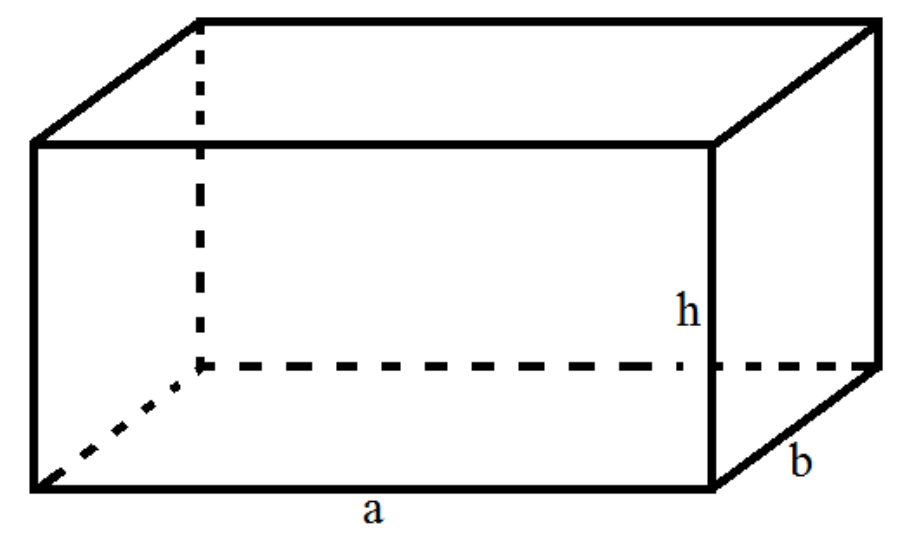
Công thức tính thể tích hình hộp chữ nhật
Thể tích hình hộp chữ nhật Nó được tính bằng chiều rộng nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
Công thức: V = axbxc
Trong đó:
- V: thể tích hình hộp chữ nhật.
- Một: chiều dài hình hộp chữ nhật.
- b: chiều rộng hình hộp chữ nhật.
- H: chiều cao hình hộp chữ nhật.
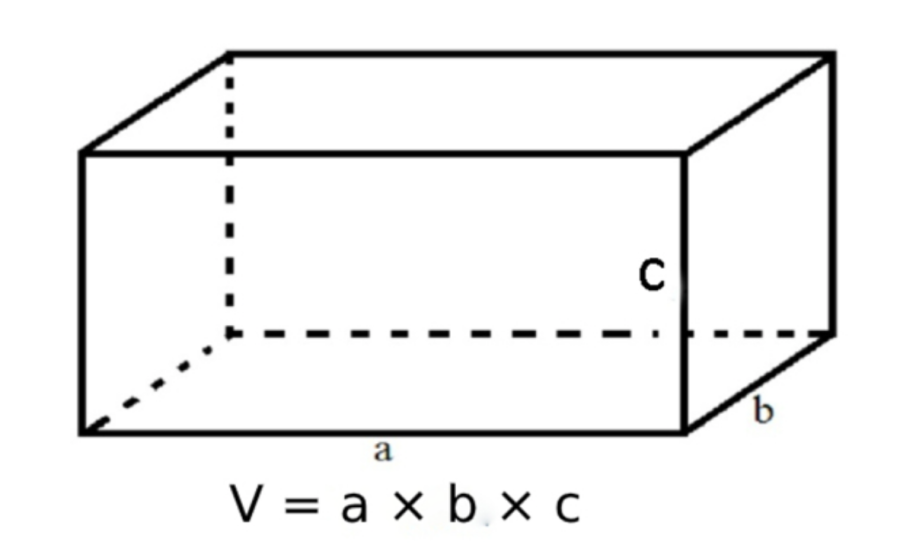
Hướng dẫn cách tính thể tích hình hộp hình chữ nhật
Để tính thể tích hình hộp chữ nhật ta làm theo các bước sau:
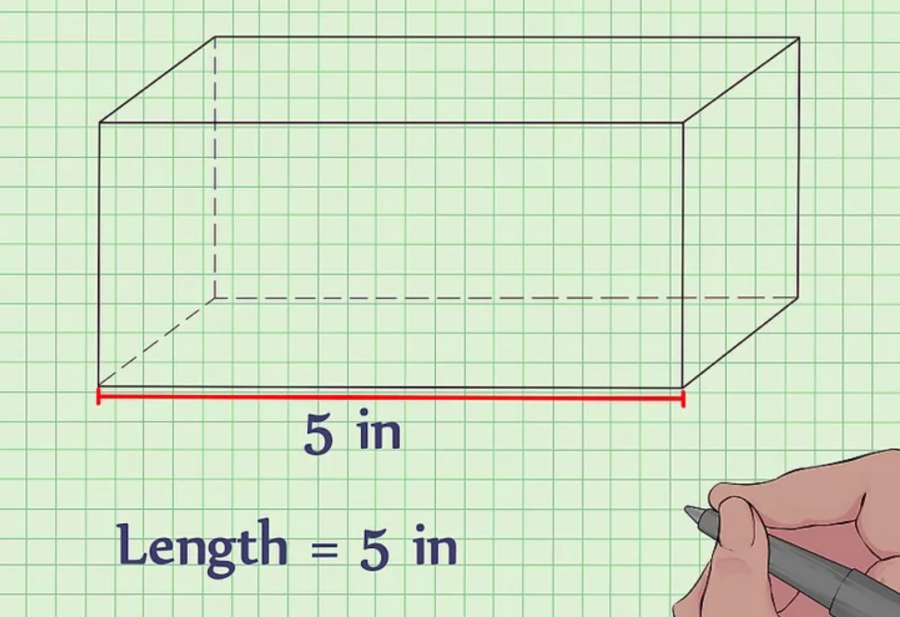
Bước 1: Đầu tiên, xác định chiều dài của hình hộp chữ nhật
Độ dài đã biết là cạnh dài nhất của mặt phẳng hình chữ nhật. Nó nằm bên trên hoặc bên dưới hộp hình chữ nhật.
Giả định: Một hình hộp chữ nhật có chiều dài = 5 cm.
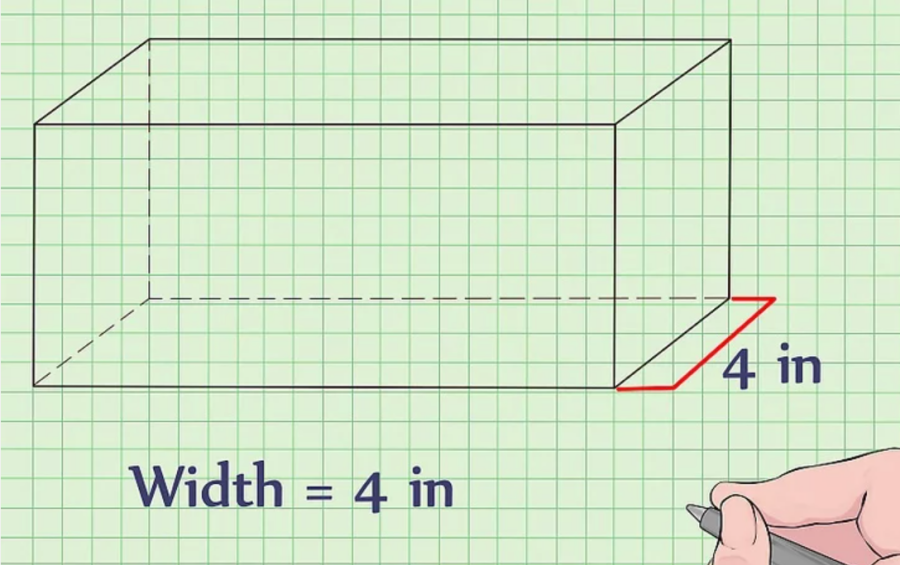
Bước 2: Sau đó các bạn xác định chiều rộng của hình hộp chữ nhật
Chiều rộng của hình hộp chữ nhật là cạnh ngắn nhất của mặt phẳng hình hộp chữ nhật. Nó cũng có thể được đặt bên trên hoặc bên dưới hộp hình chữ nhật.
Giả định: Một hình hộp chữ nhật có chiều rộng = 4 cm.
Bước 3: Tiếp theo xác định chiều cao của hình hộp chữ nhật
Chiều cao là cạnh đứng của hình hộp chữ nhật và cũng là phần nâng hình chữ nhật thành một thể tích 3 chiều.
Giả định: Một hình hộp chữ nhật có chiều cao = 3 cm.
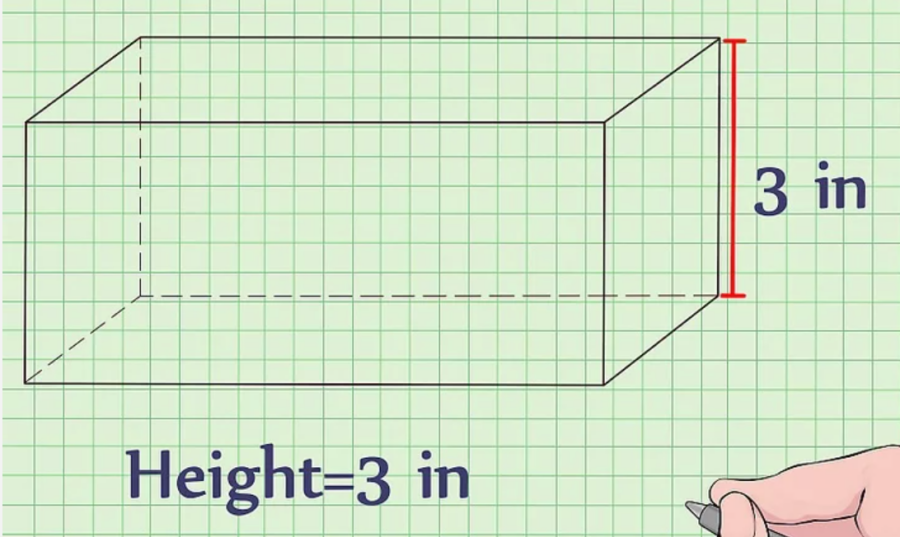
Bước 4: Tiếp theo, bạn tính tích của 3 đơn vị chiều dài, chiều rộng và chiều cao
Tại đây, bạn tiến hành nhân 3 thừa số này với nhau theo thứ tự bất kỳ mà bạn muốn sẽ ra kết quả tương tự.
Công thức tính thể tích hình hộp chữ nhật là: Thể tích (V) = chiều dài (l) * chiều rộng (w) * chiều cao (h) hoặc V=lwh.
Xét giả định trên: V = 5 (cm) * 4 (cm) * 3 (cm) = 60 (cm3).
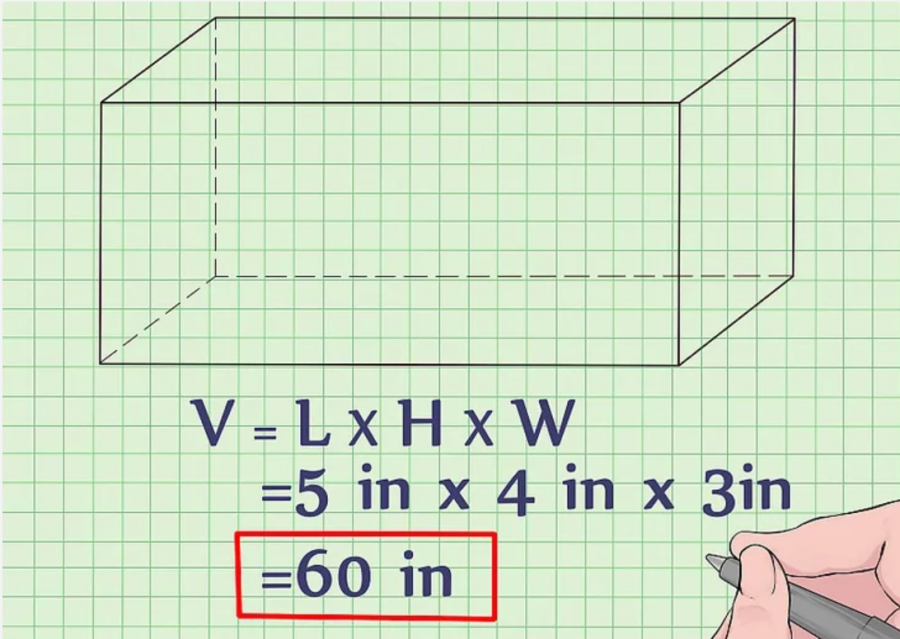
Bước 5: Cuối cùng, viết câu trả lời theo khối
Tính thể tích trong không gian ba chiều, bất kể bài toán của bạn được đưa ra theo đơn vị nào (mét, xăng-ti-mét hay xăng-ti-mét), bạn vẫn phải đưa ra đáp số theo đơn vị khối.
Xét giả định trên: Câu trả lời 60 sẽ được viết là 60 cm3.
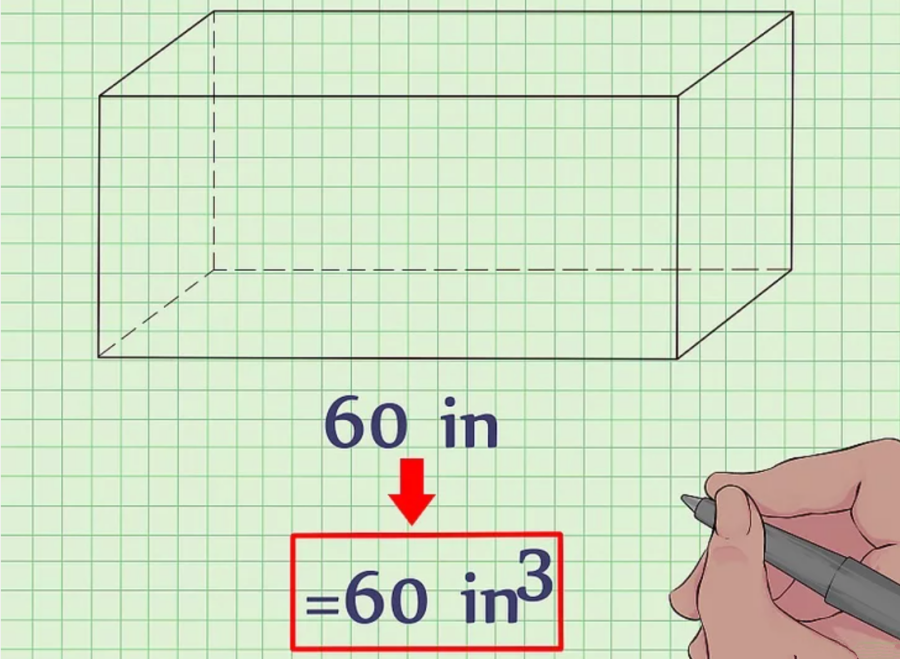
Một số bài tập tính thể tích hình hộp chữ nhật
1. Bài tập tính thể tích hình hộp chữ nhật có lời giải
Câu 1: (SGK toán lớp 5 trang 121) Tính thể tích của hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao c:
a) a = 5cm, b = 4cm, c = 9cm
b) a = 1,5m, b = 1,1m, c = 0,5m
c) a = 2/5 dm, b = 1/3 dm, c = 3/4 dm.
Phần thưởng: Thể tích của hình hộp chữ nhật trong mỗi trường hợp là:
a) V = 5 x 4 x 9 = 180 (cm³)
b) V = 1,5 x 1,1 x 0,5 = 0,825 (m³)
c) V = 2/5 x 1/3 x 3/4 = 1/10 (dm3)
Câu 2: (SGK Toán lớp 5 trang 121) Tính thể tích của hòn đá trong bể nước theo hình vẽ bên:
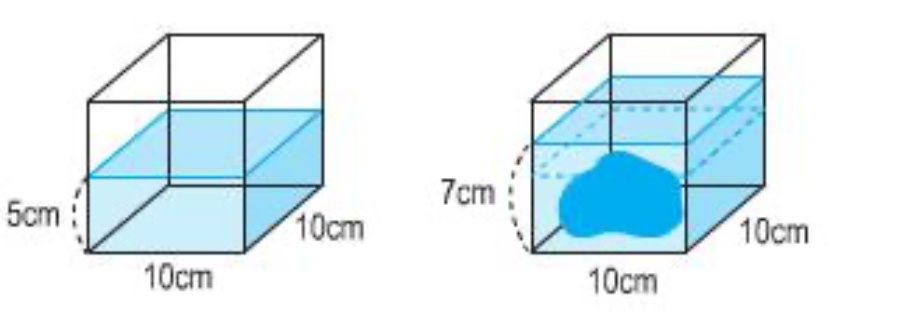
Phần thưởng:
Cách 1:
Thể tích nước trong bể là: 10 x 10 x 5 = 500 (cm3)
Tổng thể tích của nước và đá là: 10 x 10 x 7 = 700 (cm3)
Thể tích của hòn đá là: 700 – 500 = 200 (cm3)
Cách 2: Thể tích của hòn đá bằng thể tích của hình hộp chữ nhật (phần dâng lên mặt nước) có đáy bằng đáy bể và chiều cao là: 7 – 5 = 2 (cm)
Thể tích của hòn đá là: 10 x 10 x 2 = 200 (cm3)
Đáp số: 200 (cm3)
Câu 3: (SGK Toán lớp 5, trang 121) Tính thể tích của một khối gỗ có dạng như hình vẽ sau:
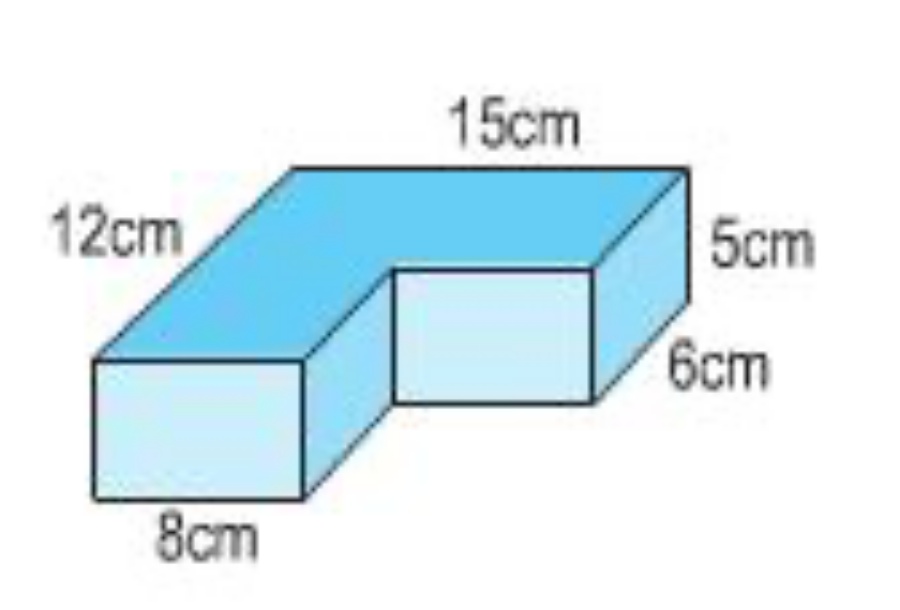
Phần thưởng: Đầu tiên, chia hình hộp chữ nhật thành hai phần: hình A và hình B
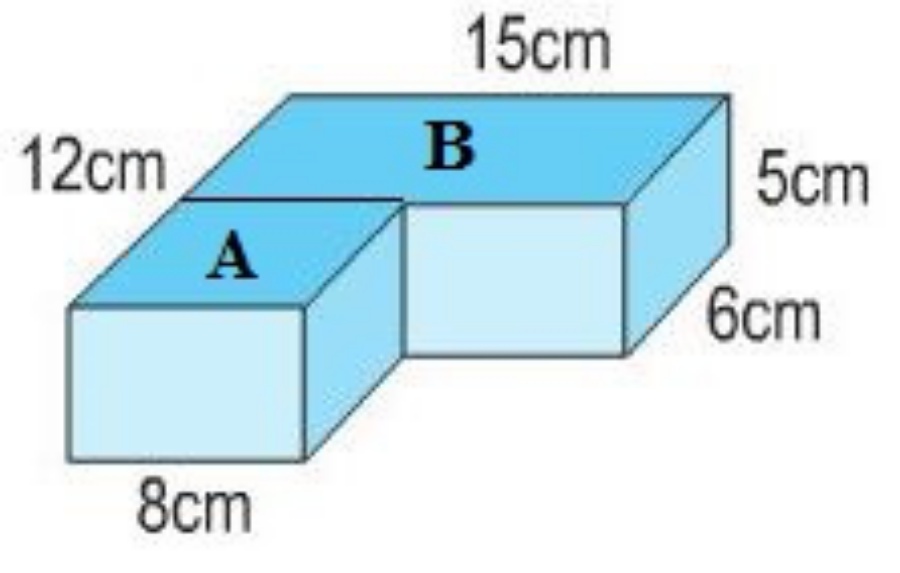
Chiều rộng hình hộp chữ nhật A là: 12 – 6 = 6 (cm)
Thể tích hình hộp chữ nhật A là: 8 × 6 × 5 = 240 (cm3)
Thể tích hình chữ nhật B là: 15 × 6 × 5 = 450 (cm3)
Thể tích của khối gỗ là: 240 + 450 = 690 (cm3)
Đáp số: 690cm3.
Câu 4: Một hình hộp chữ nhật có chiều dài 2m. Lúc đầu không có nước trong bể. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m.
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm 60 thùng nước nữa vào bể cho đầy bể. Bể cao bao nhiêu mét?
Phần thưởng:
a) Thể tích nước đổ vào bể cũng chính là thể tích của hình hộp chữ nhật có chiều dài 2m, chiều cao 0,8m.
Số lít nước đã đổ vào bể là: 120 x 20 = 2400 (lít nước)
Đổi 2400 lít nước = 2,4 m3
Diện tích đáy của bể nước là: 2,4 : 0,8 = 3 (m2)
Chiều rộng của bể nước là: 3 : 2 = 1,5 (m)
b) Tỉ số giữa mực nước dâng lên với lượng nước đổ vào đợt 1 cũng bằng tỉ số” giữa lượng nước dâng lên với lượng nước đổ vào đợt 1.
Thể tích nước đổ vào bể đợt 1:
V = 20 x 120 = 2400 (l) = 2400dm3 = 2,4m
Chiều rộng két nước: 2,4 : (2 x 0,8) = 1,5 (m)
Tỷ lệ mực nước tăng so với mực nước đổ đợt 1: V1/V2 = 60/120 = 1/2
Mực nước dâng thêm là: 0,8 x 1/2 = 0,4 (m)
Chiều cao của bể là: 0,8 + 0,4 = 1,2 (m).
Câu 5: Một cái thùng hình lập phương cạnh 7dm chứa nước có độ sâu của mực nước là 4dm. Người ta thả vào thùng 25 viên gạch có chiều dài 2dm, rộng 1dm và cao 0,5dm. Hỏi mực nước trong thùng dâng lên khỏi miệng thùng bao nhiêu cm? (Giả sử tất cả các viên gạch đều chìm trong nước và chúng hút nước không đáng kể.)
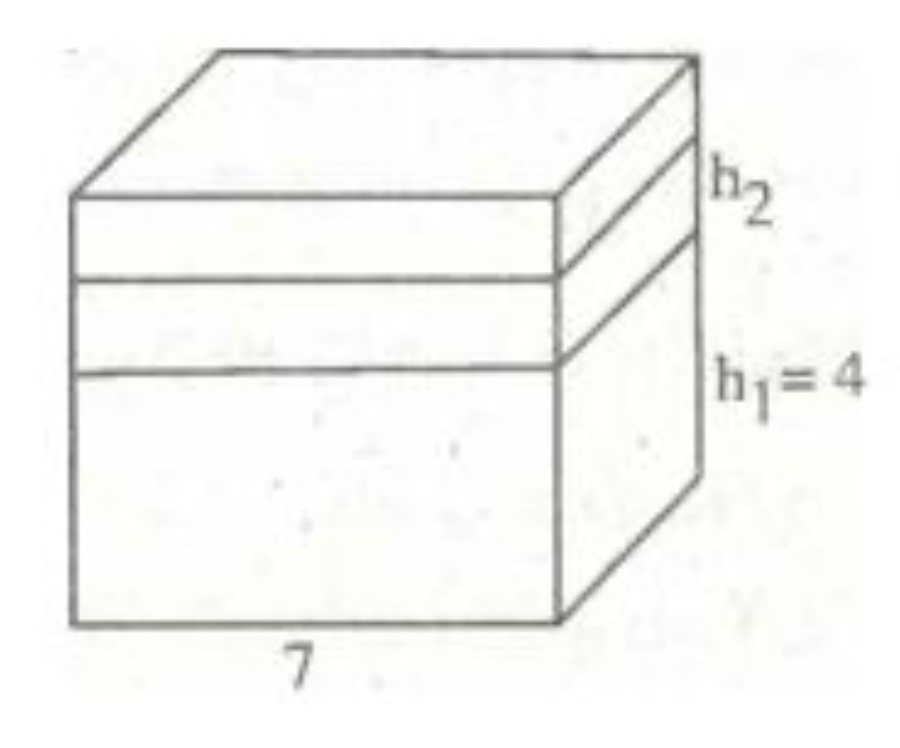
Phần thưởng: Thể tích nước trong bể lúc đầu: V1 = 7 x 7 x 4 = 196 (dm3)
Thể tích 1 viên gạch: 2,1 x 0,5 = 1 (dm3)
Thể tích 25 viên gạch: 1 x 25 = 25 (dm3)
Sau khi thả viên gạch, mực nước dâng cao hơn trước:
h = 25 : ( 7 x 7) = 25/49
Khi đó mực nước cách miệng thùng là:
7 – ( 4 + 25/49) = 122/49 (dm) ≈ 2,49 (dm)
Câu 6: Cho một hình hộp chữ nhật có chiều dài 15 cm, chiều rộng 9 cm, chiều cao 12 cm. Tính thể tích của hình hộp chữ nhật đó?
Phần thưởng:
Thể tích của miếng bìa hình chữ nhật là:
15 x 9 x 12 = 420 = 1620 (cm3)
Đáp số: 672 cm3
Câu 7: Đường chéo của các mặt của hình hộp chữ nhật lần lượt là √5,√10,√13. Tính thể tích V của hình hộp chữ nhật.
Phần thưởng:
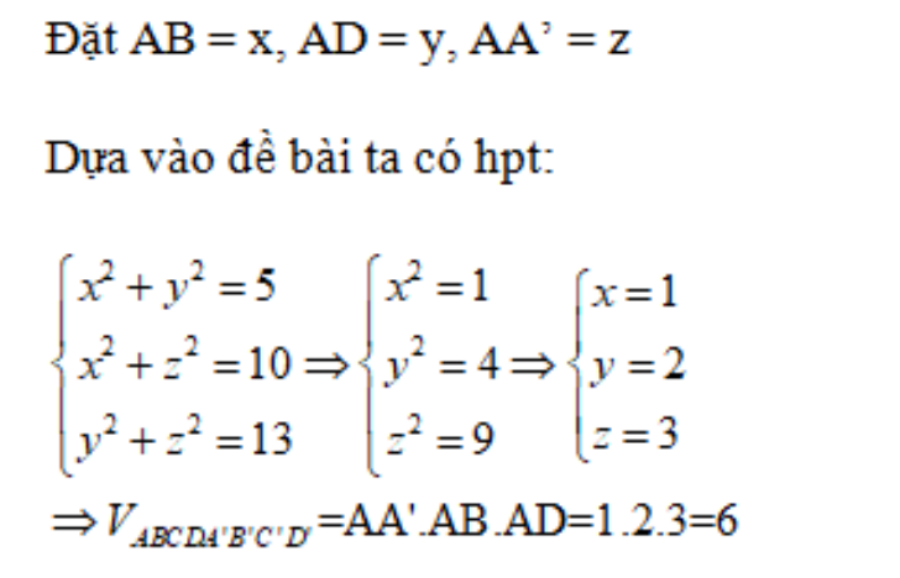
Câu 8: Cho hình lập phương ABCD.A’B’C’D có thể tích là 9. Tính thể tích tứ diện ACB’D’
Phần thưởng:

Câu 9: Tìm thể tích của hình hộp chữ nhật có chiều dài 9 cm, chiều rộng 5 cm và chiều cao 6 cm.
Phần thưởng:
Thể tích là: V = axbxc = 9 x 5 x 6 = 270 cm3
Câu 10: Một bể nước hình chữ nhật có các kích thước chiều dài đáy bể là 3m; chiều rộng nhỏ hơn chiều dài 1,8m; cao 1,5m. Hỏi bể đó đựng được nhiều nhất bao nhiêu lít nước? (1 lít = 1dm3)
Phần thưởng:
Chiều rộng của bể nước là: 3 − 1,8 = 1,2 (m)
Thể tích của bể nước đó là: V = abh = 3 × 1,2 × 1,5 = 5,4 (m3)
Vậy 5,4m3 = 5400dm3 = 5400 lít.
Vậy số lít nước lớn nhất mà bể chứa được bằng thể tích của bể và bằng 5400 lít.
2. Bài tập tính thể tích hình hộp chữ nhật không có lời giải
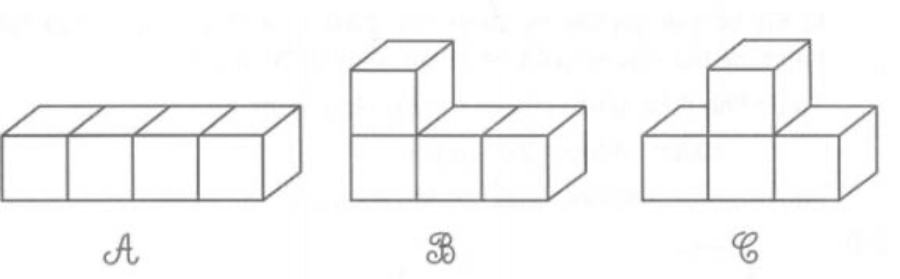
Câu hỏi 1: Tìm thể tích các hình sau có mỗi cạnh 1cm
Câu 2: Một bể cá hình chữ nhật bằng thủy tinh (không có nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 45 cm. Mực nước ban đầu trong bể cao 35 cm.
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta thả vào bể một hòn đá có thể tích 10 dm.3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng-ti-mét?
Câu 3: Tính thể tích của hình sau:
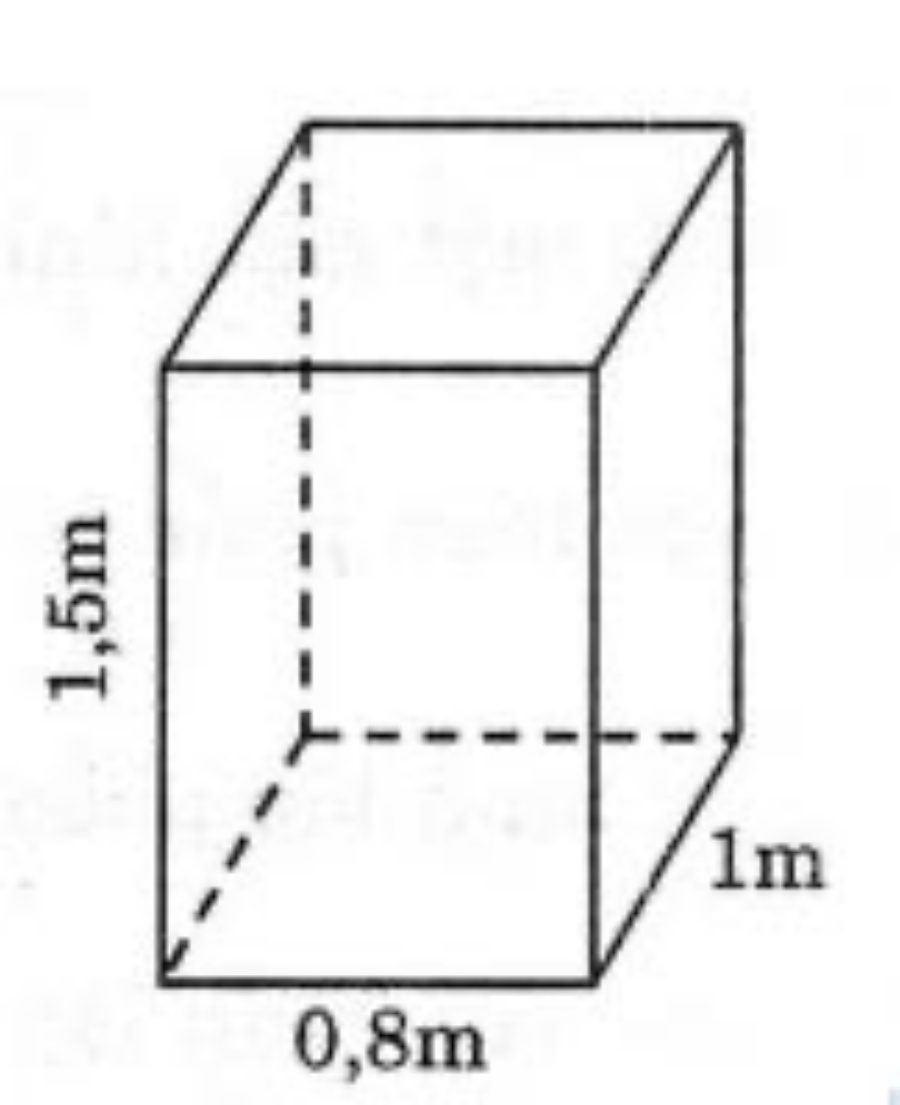
Câu 4: Tính thể tích của hình sau:
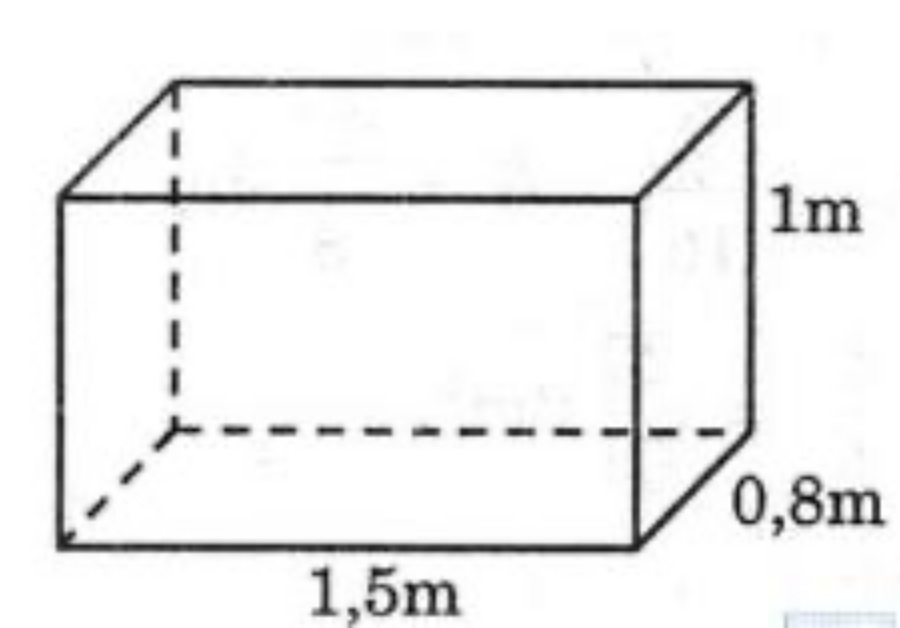
Câu 5: Tính thể tích của hình hộp chữ nhật không nắp biết chiều dài 75 cm, chiều rộng 40 cm và chiều cao 35 cm.
Câu 6: Tính thể tích hình hộp chữ nhật có diện tích xung quanh là 448 cm2chiều cao 8cm chiều dài hơn chiều rộng 4cm
Câu 7: Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao c:
a) a = 7cm; b = 5cm; C = 12cm
b) a = 3m; b = 2m; c = 1 mét
Câu 8: Một bể cá hình chữ nhật có chiều dài 90 cm, chiều rộng 50 cm và chiều cao 75 cm. Mực nước ban đầu trong bể cao 45cm. Một hòn đá có thể tích 18dm . trong bể3. Hỏi mực nước trong bể lúc này cao bao nhiêu?
Câu 9: Một bể cá hình lập phương có cạnh dài 0,8m, thể tích nước chiếm 3/4 bể. Hỏi trong bể có bao nhiêu lít nước?
Câu 10: Một hình hộp chữ nhật có tỉ số chiều dài và chiều rộng là 5/3. Chiều rộng nhỏ hơn chiều dài 36 cm. Chúng ta cũng biết rằng chiều cao là trung bình cộng của chiều dài và chiều rộng. Thể tích của chiếc hộp đó là bao nhiêu?
Trên đây là công thức tính thể tích hình hộp chữ nhật & cách tính thể tích hình hộp chữ nhật đơn giản, nhanh chóng mà nhóm INVERT chúng tôi đã tổng hợp. Hy vọng thông qua bài viết này các bạn hoàn toàn có thể tính được thể tích của hình hộp chữ nhật một cách dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%
thẻ:
tích của hình hộp chữ nhật trang 121tính tích của hình hộp chữ nhật trực tuyếnBài tập tính tích của hình hộp chữ nhậtsản phẩm của hình hộp chữ nhật lớp 5

