Không có gì ngạc nhiên khi chúng ta thường xuyên bắt gặp những đồ vật hình trụ trong cuộc sống. Bên cạnh đó, khối trụ cũng là một trong những kiến thức toán học quan trọng. Vậy hình trụ là gì, có công thức và cách tính diện tích xung quanh & diện tích toàn phần của hình trụ như thế nào?
Ngay sau đó, đội ĐẢO NGƯỢC sẽ hướng dẫn các em biết hình trụ là gì, công thức và cách tính diện tích xung quanh & tổng diện tích của hình trụ Cực kỳ chi tiết, dễ hiểu qua bài viết sau.
Mục lục bài viết [Ẩn]
một xi lanh là gì? Diện tích xung quanh & diện tích toàn phần của hình trụ?
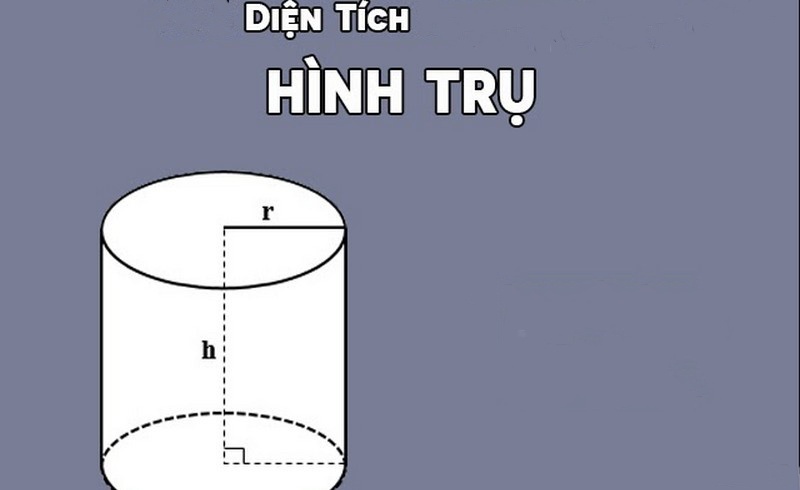
Hình trụ là loại hình không gian cơ bản, giới hạn bởi mặt trụ và 2 đáy là 2 đường tròn bằng nhau. Khi quay một hình chữ nhật quanh một cạnh cố định của hình chữ nhật đó sẽ tạo ra một hình trụ tròn xoay.
Diện tích xung quanh hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ và không bao gồm diện tích 2 đáy.
Tổng diện tích của hình trụ được tính bằng độ lớn của toàn bộ không gian hình dạng chiếm chỗ, bao gồm diện tích xung quanh và diện tích 2 đáy hình tròn.
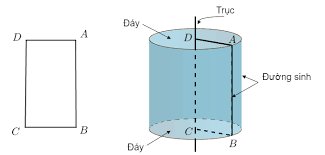
Giả sử hình chữ nhật ABCD có cạnh CD cố định thì:
- DA và CB quét nên 2 đáy của hình trụ là 2 đường tròn bằng nhau và song song, tâm của 2 đường tròn lần lượt là D và C.
- Chu vi của hình trụ quét bởi cạnh AB và mỗi vị trí của AB gọi là một đường sinh.
- Các đường sinh vuông góc với 2 mặt phẳng cơ sở (2 đường tròn).
- Chiều cao của hình trụ là độ dài trục của hình trụ (mặt bên DC) hay còn gọi là tung độ.
Công thức tính chu vi & diện tích toàn phần của hình trụ
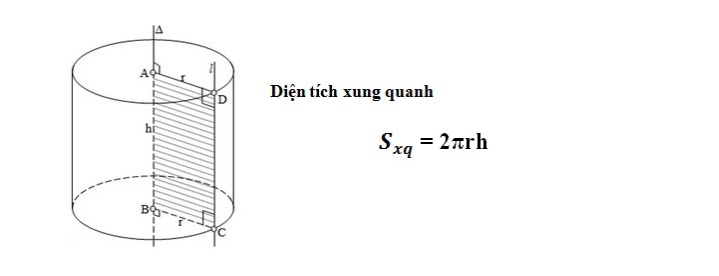
1. Công thức tính diện tích xung quanh hình trụ
Diện tích xung quanh hình trụ Nó được tính bằng chu vi của hình tròn cơ sở nhân với chiều cao.
Công thức: S (xung quanh) = 2 x π xrxh
Trong đó:
- r: bán kính hình trụ
- h: chiều cao nối đáy với đỉnh hình trụ
- = 3,14
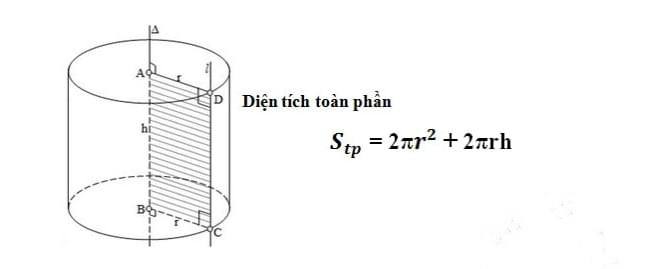
2. Công thức tính diện tích toàn phần của hình trụ
Tổng diện tích của hình trụ được tính bằng diện tích xung quanh cộng với diện tích hai đáy
Công thức: S (tổng) = 2 x π x r2 + 2 x π xrxh = 2 π xrx(r + h)
Trong đó:
- r: bán kính hình trụ
- 2 x xrxh: diện tích xung quanh hình trụ
- 2 xx r2: diện tích hai đáy
Hướng dẫn cách tính diện tích xung quanh & diện tích toàn phần của hình trụ
1. Tính diện tích 2 hình tròn (2 x (π xr .)2))
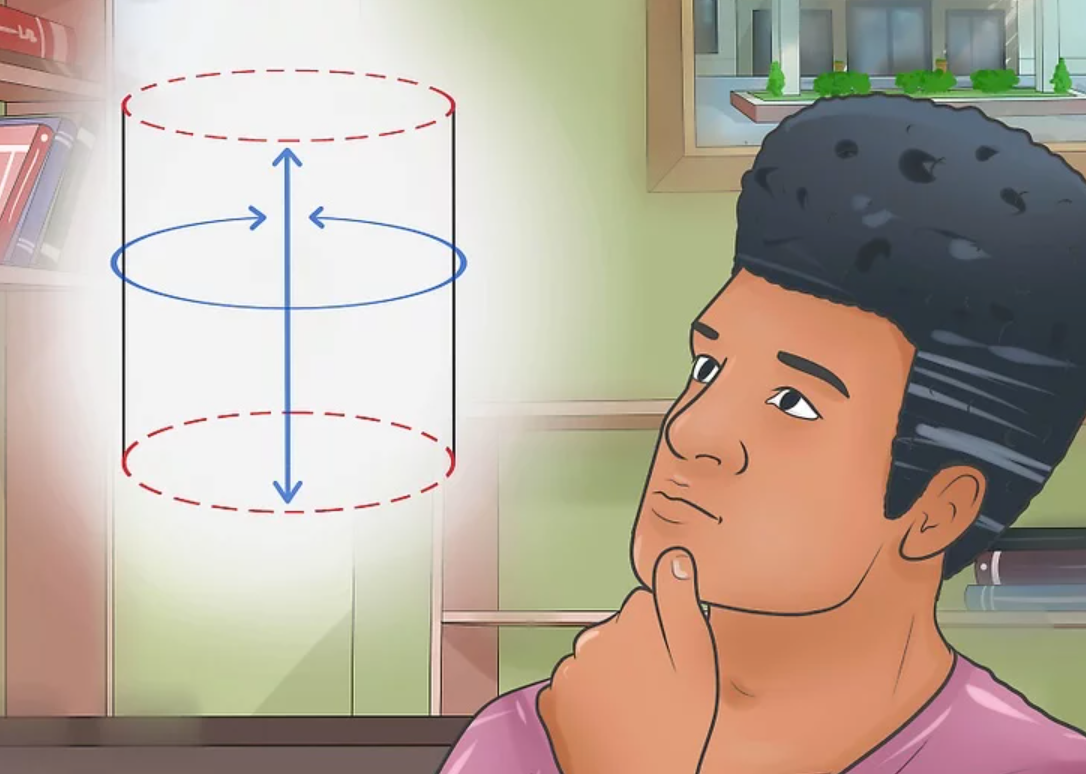
Bước 1: Đầu tiên, hình dung 2 mặt đáy của hình trụ
Hãy tưởng tượng một hình dạng với một hình trụ. Khi đó bạn sẽ thấy mặt trên và mặt dưới của nó là 2 hình tròn bằng nhau. Do đó, trước tiên bạn phải tìm diện tích của hai hình tròn này để tính diện tích toàn phần của hình trụ.
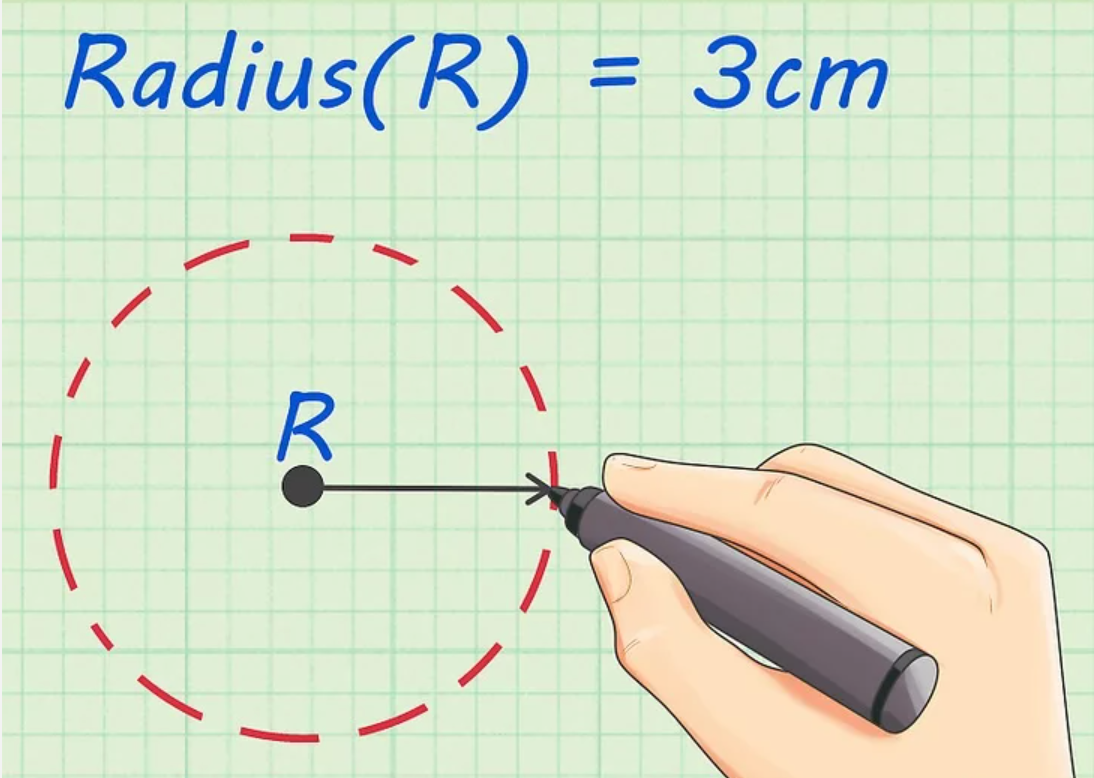
Bước 2: Sau đó các bạn tìm bán kính của hình trụ
bán kính được hiểu là khoảng cách từ tâm của đường tròn đến một điểm trên đường tròn đó và được kí hiệu là chữ “r”. Ngoài ra, bán kính của hình trụ cũng bằng bán kính của hình tròn đáy.
- Trong các bài toán đố, dữ liệu bán kính sẽ được đưa ra. Nếu không, bạn sẽ cho đường kính và bạn chỉ cần chia đôi để có bán kính.
- Trong trường hợp bạn đang tính diện tích toàn phần của một vật thể hình trụ thật, bạn cũng có thể sử dụng thước đo bán kính
Giả định: Gọi bán kính hình tròn đáy là 3 cm.
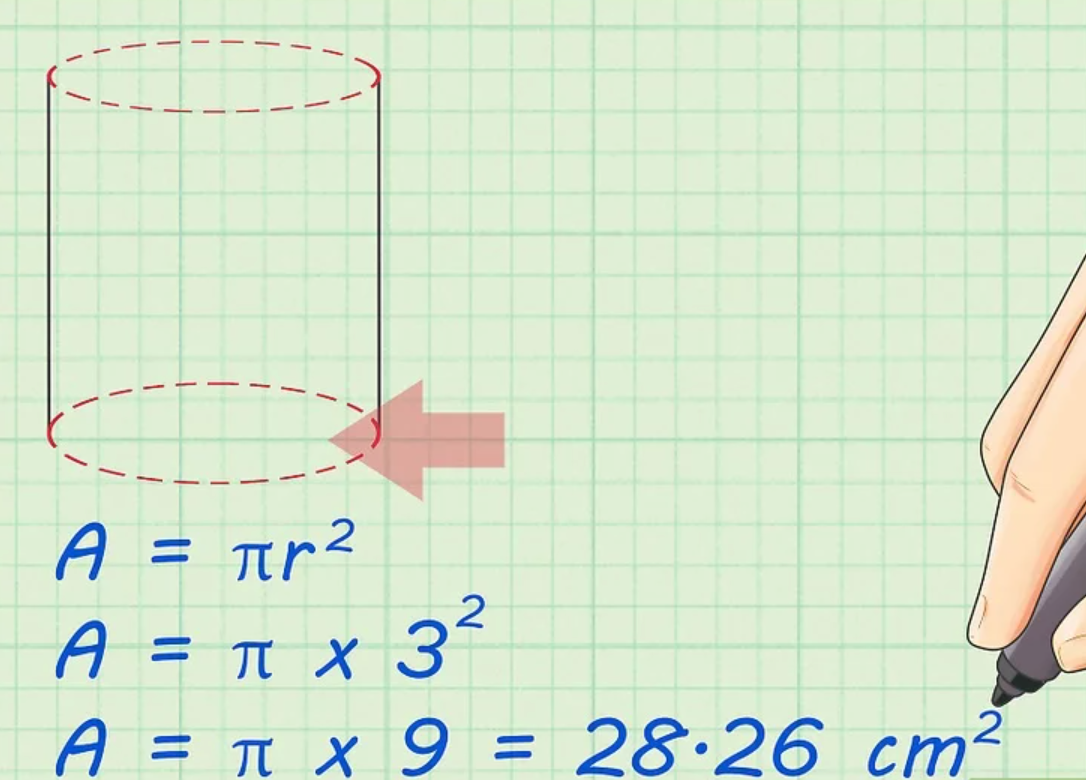
Bước 3: Tiếp theo tính diện tích hình tròn trên
Diện tích của hình tròn sẽ là pi (~3,14) nhân với bình phương bán kính của nó. Sau đó, diện tích hình tròn Được: xr2 hoặc π xrx r.
Để tìm diện tích đáy hoặc diện tích hình tròn, bạn chỉ cần thay bán kính 3 cm vào công thức: một = r2. Tiến hành như sau:
- một = r2
- Một = x 32
- A = x 9 = 28,26 cm2

Bước 4: Tiếp theo, bạn làm tương tự cho hình tròn ở đầu còn lại
Sau khi đã tìm được diện tích của 1 đáy, bạn làm tương tự với đáy thứ 2. Hoặc bạn cũng có thể áp dụng tính chất để nhận ra 2 đáy bằng nhau nên không cần tính nữa.
2. Tính diện tích thiết diện xung quanh (2π xrxh)
Bước 1: Đầu tiên, hình dung chu vi của hình trụ
Để tính diện tích xung quanh hình trụ, bạn cũng phải tưởng tượng một vật hình trụ như hộp sữa bò thường dùng để xác định mặt trên và mặt dưới. Khi đó, bán kính của thành hộp sữa cũng chính là bán kính của đáy nhưng khác đáy vì thành xung quanh cũng có chiều cao.
Bước 2: Tiếp theo tìm chu vi hình tròn
Khi bạn đã hình dung được chu vi của hình trụ, bạn cần tìm chu vi để tìm diện tích của mặt xung quanh. Bạn tìm chu vi bằng cách nhân bán kính với 2π.
Theo ví dụ trên: Chu vi của hình trụ bằng: 2π. 3 cm x 2π = 18,84 cm.

Bước 3: Sau đó các bạn nhân chu vi hình tròn với chiều cao hình trụ
Tại đây, bạn tiếp tục nhân chu vi tính được với chiều cao để ra diện tích các mặt xung quanh.
Xét một ví dụ: Hình trụ có chiều cao là (5 cm): 18,84 cm x 5 cm = 94,2 cm2.

3. Cộng hai kết quả lại với nhau ((2) x ( xr2)) + (2π xrxh)
Bước 1: Đầu tiên, hình dung toàn bộ hình trụ
Trước khi bắt đầu tính toán, bạn cần hình dung 2 đáy của hình trụ. Sau đó tiếp tục tính thiết diện xung quanh nối hai đáy của hình trụ. Chỉ sau đó, bạn mới nghĩ về toàn bộ hình trụ và tính diện tích toàn bộ bề mặt của nó.
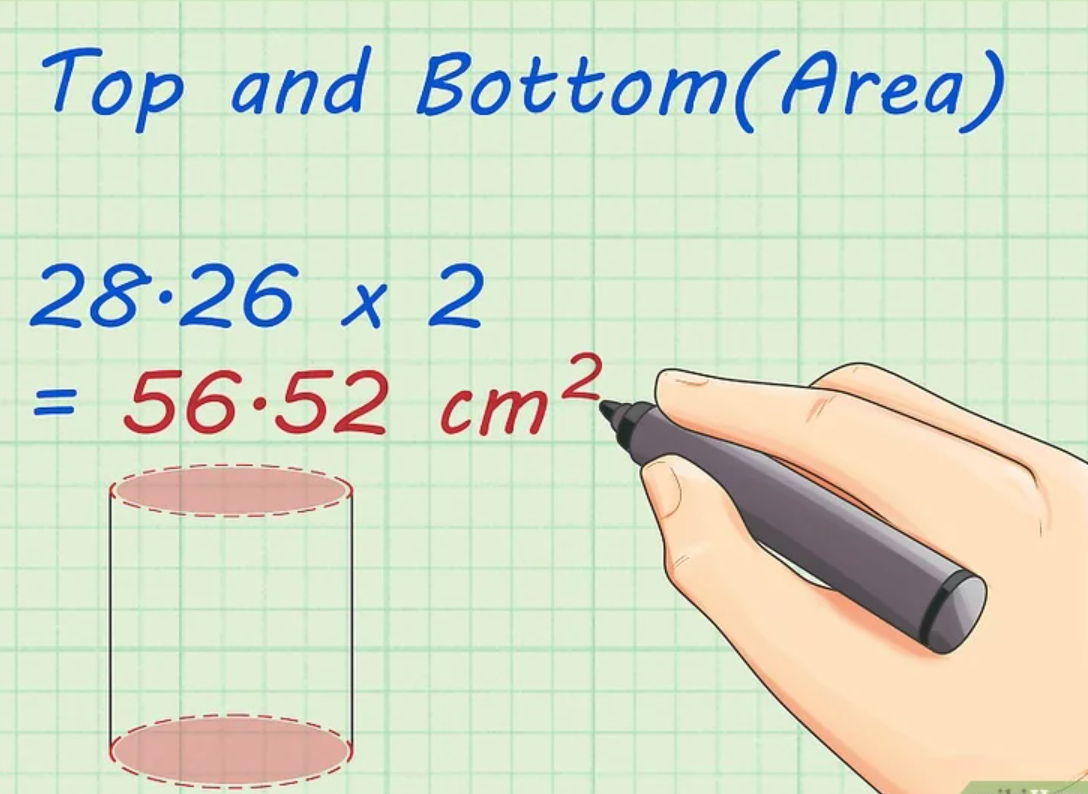
Bước 2: Tiếp theo, bạn nhân đôi diện tích của 1 căn
Sau khi đã hình dung được hình trụ, bạn tiến hành nhân kết quả diện tích 1 đáy 28,26 cm2 với 2 được diện tích 2 đáy là: 28,26 x 2 = 56,52 cm2.
Bước 3: Cuối cùng, thêm diện tích của mặt xung quanh vào diện tích của đế.
Tổng diện tích hình trụ thu được sẽ hiển thị khi bạn cộng diện tích của hai đáy với diện tích bề mặt xung quanh.
Lấy ví dụ trên: Diện tích toàn phần của hình trụ có chiều cao 5 cm và đáy là hình tròn bán kính 3 cm là: 56,52 cm2 + 94,2cm2 = 150,72cm2.

Một số bài tập tính diện tích xung quanh & diện tích toàn phần của hình trụ
1. Bài tập tính diện tích xung quanh & diện tích toàn phần của hình trụ có lời giải
Câu 1: Một hình trụ có chu vi đáy là 20 cm, diện tích xung quanh là 14 cm.2. Tính chiều cao của hình trụ?
Phần thưởng:
Diện tích xung quanh của hình trụ: Sxq = 2 x xrxh = 20 xh = 14
→ h = 0,7 (cm)
Câu 2: Tính diện tích toàn phần của hình trụ có đáy là 10 cm và khoảng cách giữa hai đáy là 6 cm.
Phần thưởng:
Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm.
Áp dụng công thức tính diện tích toàn phần của hình trụ:
Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)
=> Vậy diện tích toàn phần của hình trụ là 110π(cm2)
Câu 3: Tính diện tích toàn phần của hình trụ có chiều cao là 7cm và diện tích xung quanh là 310 (cm .).2)
Phần thưởng: Theo đề bài ta có: h = 7, Sxq = 310
Áp dụng công thức tính diện tích xung quanh Sxq = 2πrh
⇒ r= (Sxq) : 2πrh = 310 : 2π.7 ≈ 7cm
Vậy SD = r2 = .72 = 49π 154cm2
Diện tích toàn phần hình trụ: Stp = 2. Sd + Sxq = 2,154 + 310 = 618cm2
Câu 4: Cho một hình trụ có bán kính đường tròn đáy là 4 cm, chiều cao nối từ đáy đến đỉnh của hình trụ là 6 cm. Tính chu vi và diện tích toàn phần của hình trụ?
Phần thưởng:
Diện tích xung quanh là Sxq = 2πrh = 2 x 3,14 x 4 x 6 = 151 cm²
Diện tích toàn phần của hình trụ là: Stp = 2TR x (R + H) = 2 x 3,14 x 4 x (4 + 8) = 301 cm².
Câu 5: Tính diện tích toàn phần của hình trụ có đáy là 10 cm và khoảng cách giữa hai đáy là 6 cm.
Phần thưởng: Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm .
Diện tích toàn phần của hình trụ : Stp = 2πr( r + h ) = 2.5( 5 + 6 ) = 110 (cm²)
Kết luận: Diện tích toàn phần của hình trụ là 110r ( cm3 )
Câu 6: Một đèn huỳnh quang dài 1,2m, đường kính vòng tròn đáy 4cm, được đặt vừa khít trong một ống giấy cứng hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm hộp.
Phần thưởng: Diện tích tờ giấy cứng cần tính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích xung quanh của hình hộp chính là diện tích của 4 hình chữ nhật bằng nhau có chiều dài 120 cm, chiều rộng 4 cm: Sxq = 4. 4. 120 = 1920 cm2
Câu 7: Một hình trụ có bán kính đáy là 7cm, diện tích xung quanh là 352cm2. Chiều cao của hình trụ là bao nhiêu?
Phần thưởng:
Ta có: Sxq = 2πrh
⇒ h = Sxq : 2πr
Với S = 352 cm2r = 7cm
⇒ h = 352 : 2π7 ≈ 8 (cm)
Câu 8: Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Chu vi của hình trụ là 314 cm2. Tính bán kính của đường tròn cơ sở (làm tròn kết quả đến chữ số thập phân thứ hai).
Phần thưởng:
Diện tích xung quanh hình trụ là 314cm2
2.π.rh = 314
Rằng r = h
2πr2= 314
r2 50
⇒ r ≈ 7,07 (cm)
Câu 9: Một đèn huỳnh quang dài 1,2m, đường kính vòng tròn đáy là 4cm, được đặt vừa khít trong một ống các tông hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm hộp (Hộp hở 2 đầu, không kể lề và các cạnh đã dán).
Phần thưởng: Diện tích tờ giấy cứng cần tính là diện tích xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Chu vi hình lập phương là diện tích của bốn hình chữ nhật bằng nhau có chiều dài 120 cm và chiều rộng 4 cm:
Sxq= 4,4.120 = 1920 cm2
Câu 10: Tính chu vi của một hình trụ có chu vi đáy là 13cm, chiều cao là 3cm.
Phần thưởng:
Ta có: C = 13cm, h = 3cm
Chu vi của hình trụ là:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm2)
2. Bài tập tính diện tích xung quanh & diện tích toàn phần của hình trụ không lời giải
Câu hỏi 1: Cho một hình trụ có chu vi đáy 8π và chiều cao h = 10. Tính chu vi & diện tích toàn phần của hình trụ?
Câu 2: Cho một hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là bao nhiêu?
Câu 3: Cho một hình trụ có bán kính đáy R = 8cm và diện tích toàn phần là 564π cm2. Tính chiều cao của hình trụ:
Câu 4: Hộp sữa Ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm, đường kính đáy h = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy 3,14
Câu 5: Một hình trụ có bán kính đáy R = 2cm và diện tích xung quanh Sxq = 100π . Tính diện tích toàn phần của hình trụ?
Câu 6: Tìm chu vi của một hình trụ có chu vi đáy là 4π và chiều cao h = 2.
Câu 7: Cho một hình trụ có bán kính đáy R = 12 cm và diện tích toàn phần 672π cm2. Tính chiều cao của hình trụ
Câu 8: Diện tích và chu vi hình chữ nhật ABCD (AB > AD) lần lượt là 2a2 và 6a. Cho hình chữ nhật quay quanh cạnh AB một lần ta được hình trụ. Tính chu vi hình trụ này
Câu 9: Mô hình lọ thí nghiệm hình trụ (không có nắp) bán kính đáy 14 cm, chiều cao 10 cm. Diện tích xung quanh cộng với diện tích của một cơ sở là gì?
Câu 10: Chu vi hình trụ là 10m2 và diện tích toàn phần là 14m2. Tính bán kính đường tròn đáy và chiều cao của hình trụ (lấy = 3,14, làm tròn kết quả đến 2 chữ số thập phân)
Trên đây là Công thức tính chu vi & diện tích toàn phần hình trụ mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này các bạn hoàn toàn có thể tính được diện tích xung quanh & diện tích toàn phần của hình trụ một cách dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%
thẻ:
công thức tính diện tích toàn phần của hình trụchu vi của hình trụdiện tích xung quanh hình tròn

