Định lý Pytago là một trong những kiến thức Toán học quan trọng, nhất là đối với các bạn học sinh lớp 7. Vậy Định lý Pytago là gì và công thức tính định lý Pytago là như thế nào?
Đừng lo, đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn biết Định lý Pytago là gì và công thức tính định lý Pytago đơn giản, chi tiết, dễ hiểu thông qua bài viết sau.
Mục lục bài viết [Ẩn]
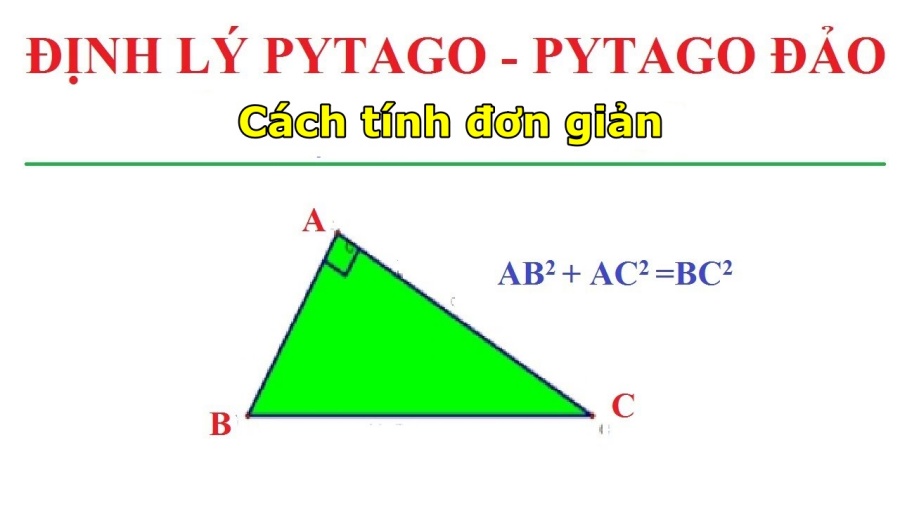
Định lý Pytago là gì?
Trong hình học, định lý Pytago (định lý Pythagoras) là mối liên hệ căn bản trong hình học Euclid giữa 3 cạnh của 1 tam giác vuông.
Mặc dù mối quan hệ giữa các cạnh trong tam giác vuông đã được con người phát hiện từ trước thời cổ đại. Tuy nhiên, mãi đến thời Hy Lạp, định lý này mới được nhà toán học Pythagoras (580 – 490 TCN) chứng minh và ứng dụng rộng rãi trong nhiều lĩnh vực như: Toán vi phân, tích phân, hình học không gian,… Có thể nói Pytago ra đời đánh dấu thành tựu phát triển nền toán học nhân loại.
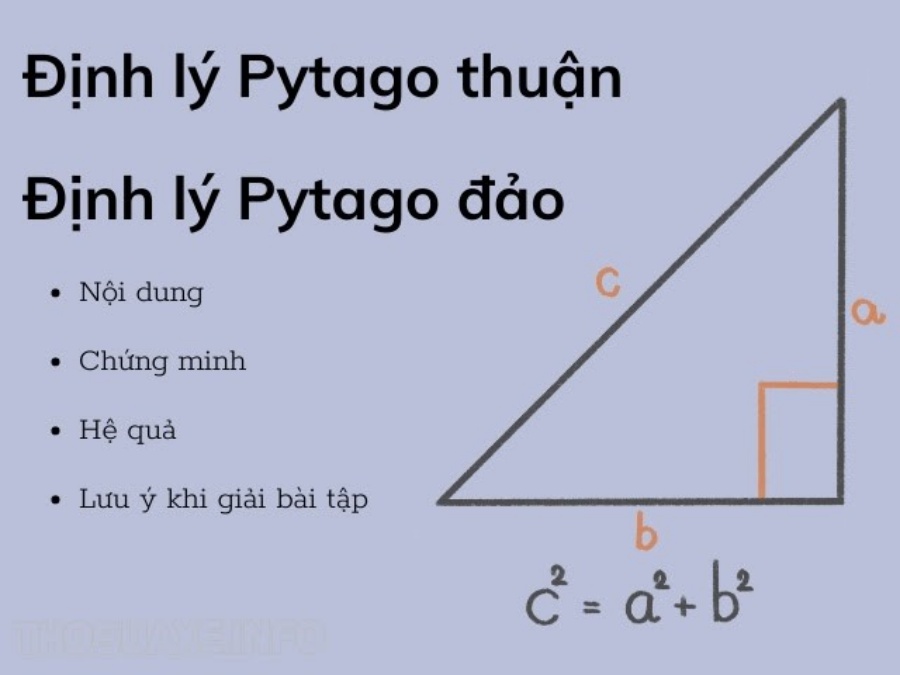
- Định lý Pytago thuận: Trong một tam giác vuông bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
- Định lý Pytago nghịch: Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
Định lý Pytago dùng để làm gì? Định lý Pytago còn được dùng để dựng đoạn thẳng vô cước, biểu hiện độ dài của các cạnh của một tam giác vuông mà cả ba độ dài này là những số nguyên dương.

Công thức định lý Pytago
1. Định lý Pytago thuận
Định lý Pytago thuận: Trong một tam giác vuông bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
Hay: Tổng diện tích của hai hình vuông có cạnh là hai cạnh vuông của tam giác vuông (a và b) bằng diện tích của hình vuông có cạnh là cạnh huyền (c).\
Cho tam giác ABC vuông tại A. Có độ dài cạnh AB = a, AC = b, BC = c. Áp dụng định lý Pytago, công thức về mối liên hệ giữa các cạnh trong tam giác được biểu diễn như sau:
Tam giác ABC vuông tại A thì ta có: BC² = AB² + AC²
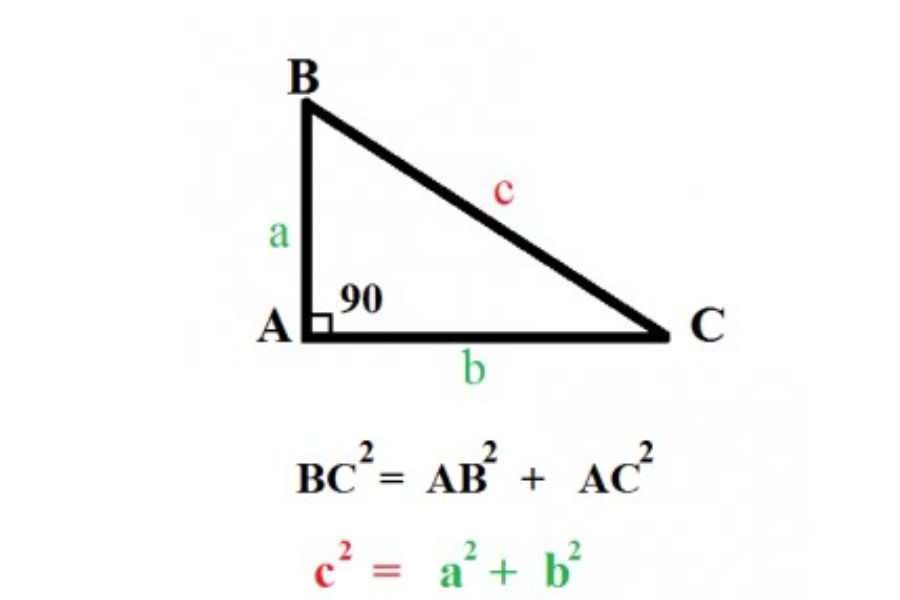
Trong đó:
- BC (c): Độ dài cạnh huyền
- AB, AC (a,b): Độ dài 2 cạnh góc vuông
Ví dụ: Cho tam giác ABC vuông tại A có 2 cạnh góc vuông AB, AC lần lượt bằng 6 và 8 cm. Tính độ dài cạnh BC
Giải: Áp dụng định lí Pytago trong tam giác vuông ABC, ta có:
BC² = AB² + AC²
=> BC² = 62 + 82 = 36 + 64 = 100
BC² = 62 + 82 = 36 + 64 = 100
Vậy BC = 10 cm
Chú ý: Dựa vào định lí Pytago, khi biết độ dài 2 cạnh góc vuông trong tam giác vuông thì bạn sẽ tính được độ dài của cạnh còn lại.
2. Định lý Pytago đảo
Định lý Pytago nghịch: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Tam giác ABC có BC² = AB² + AC² => Góc BAC = 90°
Sử dụng định lý Py-ta-go đảo để nhận biết tam giác vuông
Phương pháp:
- Tính bình phương các độ dài ba cạnh của tam giác
- So sánh bình phương của cạnh lớn nhất với tổng các bình phương của hai cạnh kia
- Nếu hai kết quả bằng nhau thì tam giác đó là tam giác vuông, cạnh lớn nhất là cạnh huyền.
Ví dụ: Cho tam giác ABC có AC= 5 cm, BC= 3 cm, AB= 4 cm. Tam giác ABC là tam giác gì?
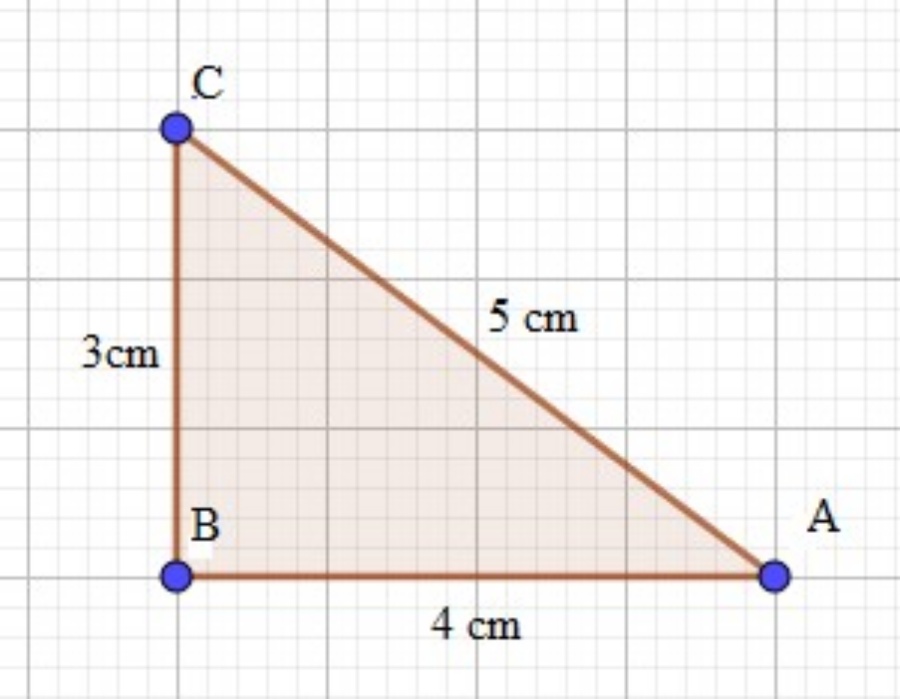
Giải: Ta có: AC² = BC² + AB² ( vì 5² = 3² + 4²)
Nên tam giác ABC vuông tại B( Định lí Pytago đảo)
Chú ý: Cạnh huyền là cạnh lớn nhất trong tam giác vuông
Cách chứng minh định lý Pytago
1. Chứng minh định lý Pytago thuận
Qua hình dưới đây, bạn có thể chứng minh định lý Pytago thuận bằng cách:
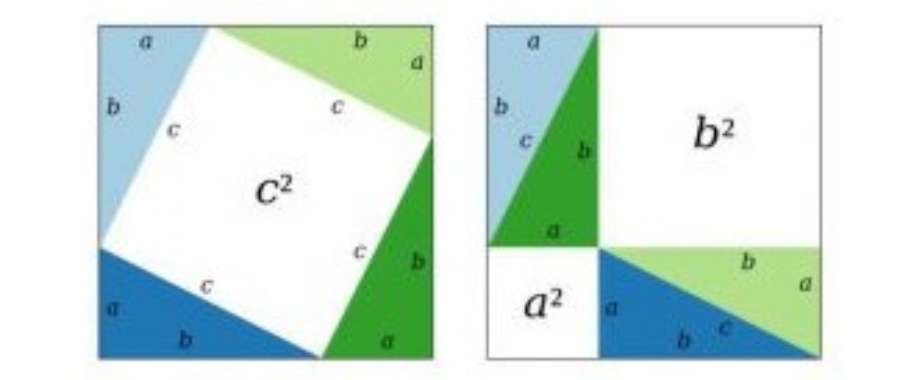
Chứng minh: Ở hình trên ta có 2 hình vuông lớn có diện tích bằng nhau là: (a+b)2
Trong mỗi hình lại có 4 tam giác vuông bằng nhau có diện băng nhau là 1/2(a.b). Do đó diện tích khoảng trắng của 2 hình sẽ bằng nhau.
Như vậy, diện tích của hình vuông c sẽ bằng tổng diện tích của 2 hình vuông a và b nên ta có: c2=a2+b2
2. Chứng minh định lý Pytago đảo
Định lý Pytago đảo được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn. Đây là một định lý toán học quan trọng hàng đầu của hình học cơ bản.
Ví dụ: Tam giác ABC có BC2 = AB2 + AC2 => tam giác ABC bằng 90o
Chứng minh: Gọi ABC là tam giác với các cạnh a, b, và c, với a² + b² = c².
- Dựng một tam giác thứ hai có các cạnh bằng a và b và góc vuông tạo bởi giữa chúng.
- Theo định lý Pytago thuận, cạnh huyền của tam giác vuông thứ hai này sẽ bằng c=√(a²+b²) và bằng với cạnh còn lại của tam giác thứ nhất.
- Bởi vì cả hai tam giác có ba cạnh tương ứng cùng bằng chiều dài a, b và c, do vậy hai tam giác này phải bằng nhau.
- Do đó góc giữa các cạnh a và b ở tam giác đầu tiên phải là góc vuông.
Ngoài ra, bạn cũng có thể chứng minh định lý pytago đảo mà không cần sử dụng tới định lý thuận.
3. Chứng minh định lý Pytago trong tam giác vuông
Một hệ quả của định lý Pytago đảo đó là cách xác định đơn giản một tam giác có là tam giác vuông hay không, hay nó là tam giác nhọn hoặc tam giác tù. Gọi c là cạnh dài nhất của tam giác và có a + b > c (nếu không sẽ không tồn tại tam giác vì đây chính là bất đẳng thức tam giác). Các phát biểu sau đây là đúng:
- Nếu a² + b² = c², thì tam giác là tam giác vuông.
- Nếu a² + b² > c², nó là tam giác nhọn.
- Nếu a² + b² < c², thì nó là tam giác tù.
4. Chứng minh định lý Pytago trong tam giác cân
Theo định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh bằng nhau gọi là hai cạnh bên, cạnh còn lại gọi là cạnh đáy.
- Tam giác ABC có AB = AC = A => Tam giác ABC cân tại A.
- Trong một tam giác cân, hai góc ở đáy bằng nhau.
- Tam giác ABC cân tại A => góc B = góc C.
Muốn chứng minh một tam giác là tam giác cân, ta cần chứng minh tam giác đó có hai cạnh bằng nhau hoặc hai góc bằng nhau.
- Tam giác đều là tam giác có ba cạnh bằng nhau.
- Trong một tam giác đều, ba góc bằng nhau và bằng 60.
- Tam giác ABC có AB = AC=BC = A ABC là tam giác đều.
- Tam giác ABC là tam giác đều = A = B= E = 600
5. Chứng minh định lý Pytago trong tam giác đều
Muốn chứng minh một tam giác là tam giác đều, ta cần chứng minh:
- Tam giác có ba cạnh bằng nhau.
- Hoặc chứng minh tam giác có ba góc bằng nhau.
- Hoặc chứng minh tam giác cân có 1 góc bằng 60.
Định lí Pitago thuận: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
Cách áp dụng định lý Pitago
Để có thể vận dụng vào các dạng bài tập, dưới đây là cách áp dụng định lý Py-ta-go lớp 7 bạn nên biết:
– Tìm cạnh tam giác vuông
- Công thức Pitago được dùng để áp dụng với các trường hợp tam giác vuông đi tìm các cạnh thì các bạn phải có giả thuyết là tam giác vuông với góc 90 độ.
- Qua hình vẽ sẽ xác định được 2 cạnh góc vuông và cạnh huyền. Cạnh huyền sẽ đối diện với góc vuông và có chiều dài nhất còn cạnh ngắn nhất là 2 cạnh góc vuông.
- Với định lý Pitago, để tính được độ dài cạnh trong tam giác vuông thì cần phải biết được chiều dài hai cạnh còn lại.
- Thay 2 giá trị của 2 cạnh theo công thức a² + b² = c²
- Tính bình phương các cạnh đã biết, bạn hãy để ở dạng mũ và thực hiện phép tính bình thường.
- Tách biến sang một vế của phương trình bạn cần tính.
- Giảm bình phương của cả hai vế
- Dùng định lý Pitago tìm cạnh tam giác vuông.
– Tính khoảng cách giữa hai điểm trong mặt phẳng x y
- Bước đầu tiên, bạn phải xác định 2 điểm trong mặt phẳng XY. Với định lý Pytago, bạn có thể dễ dàng tính được khoảng cách của hai điểm. Tọa độ x, y sẽ được viết ra 1 cặp tọa độ (x,y)
- Vẽ hai điểm trên đồ thị trên đồ thị tọa độ (x, y) sẽ luôn được gắn liền với trục hoành và trục tung.
- Tìm độ dài các cạnh góc vuông của tam giác.
- Dùng định lý Pitago để giải phương trình rồi ra cạnh huyền
– Cách sử dụng định lý Pytago chi tiết
1. Tìm các cạnh của tam giác vuông
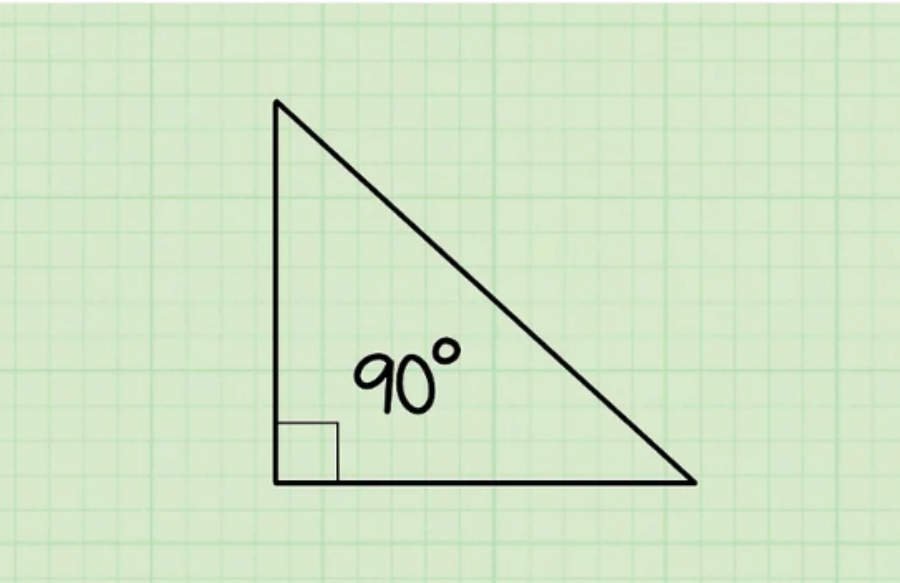
Bước 1: Hãy chắc chắn rằng tam giác của bạn là một tam giác vuông.
Định lý Pytago chỉ áp dụng cho các tam giác vuông. Do đó, trước khi tiến hành, cần chắc chắn rằng tam giác của bạn đáp ứng đủ tiêu chí của một tam giác vuông.
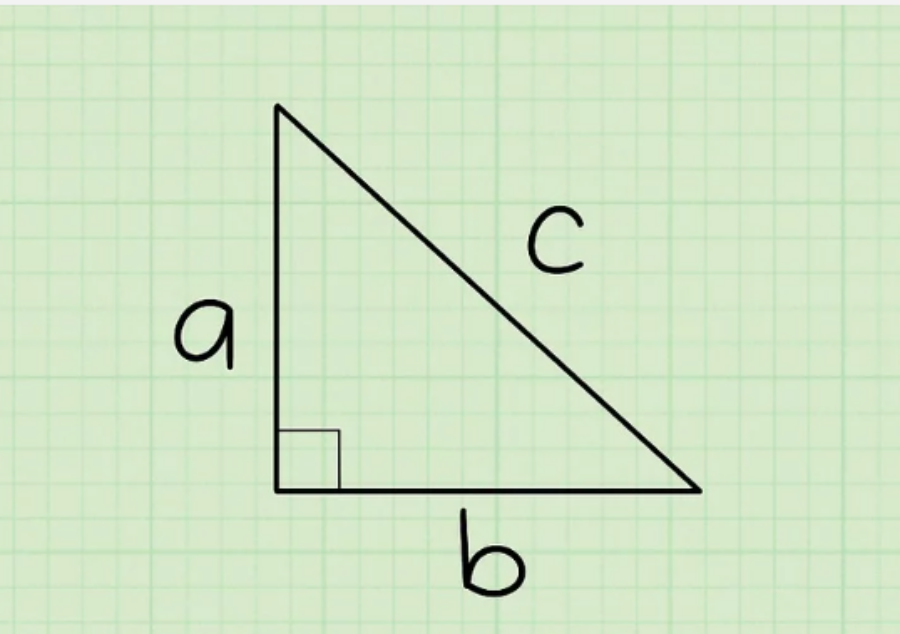
Bước 2: Gọi các cạnh tam giác là a, b, và c.
Trong Định lý Pytago, a và b là các cạnh góc vuông, c là cạnh huyền (cạnh dài nhất luôn luôn đối diện với góc vuông). Vậy nên, để bắt đầu, gọi các cạnh ngắn hơn của tam giác là a và b (không quan trọng cạnh nào là ‘a’ hoặc ‘b’), và gọi cạnh huyền là c.
Bước 3: Xác định bạn cần tìm cạnh nào của tam giác.
Theo định lý Pytago, cho phép tìm độ dài của bất kỳ 1cạnh nào của tam giác vuông miễn biết chiều dài 2 cạnh còn lại.
- Ví dụ, bạn biết cạnh huyền có chiều dài là 5 và một trong các cạnh bên có chiều dài là 3. Tuy nhiên, bạn không biết độ dài của cạnh thứ 3 là bao nhiêu. Khi đó, bạn sẽ giải bài toán tìm cạnh thứ ba, vì đã biết độ dài của hai cạnh còn lại.
- Nếu độ dài hai cạnh là chưa biết, bạn cần xác định độ dài của một cạnh nữa để sử dụng Định lý Pythagore. Khi đó, các hàm lượng giác cơ bản có thể giúp bạn nếu bạn biết số đo 1 trong những góc nhọn của tam giác.
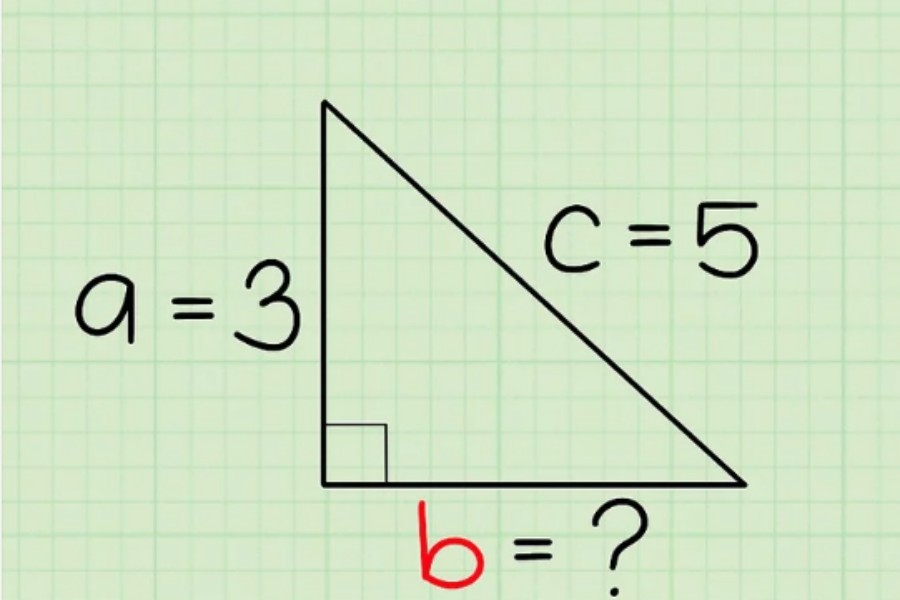
Bước 4: Thay hai giá trị đã biết vào phương trình.
Thay giá trị độ dài các cạnh của tam giác vào phương trình a2 + b2 = c2. Nhớ rằng a và b là hai cạnh góc vuông, c là cạnh huyền.
Ví dụ: Bạn biết độ dài 1 cạnh và cạnh huyền (là 3 và 5) => phương trình sẽ là 3² + b² = 5²
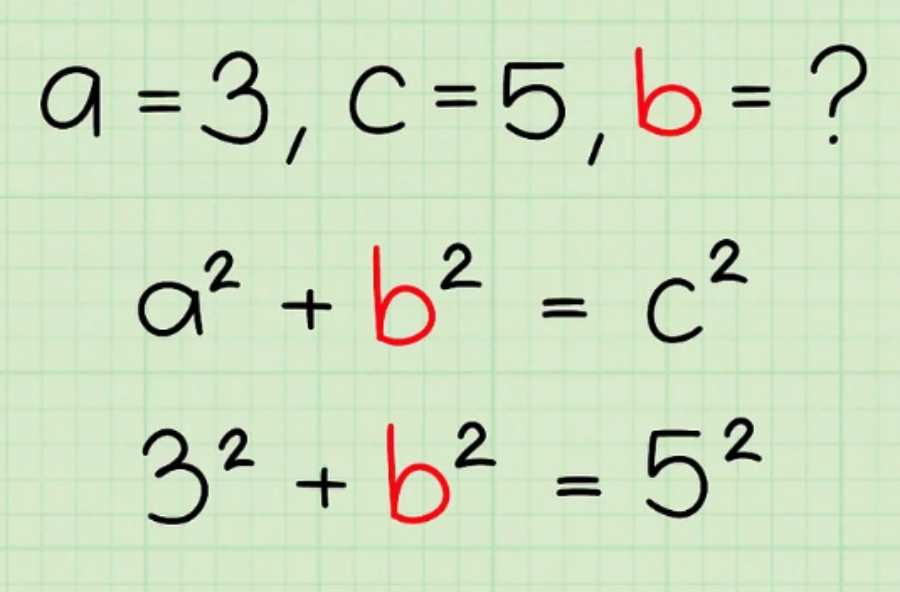
Bước 5: Tính bình phương.
Để giải phương trình, hãy bắt đầu bằng cách lấy bình phương của mỗi cạnh đã biết. Ngoài ra, nếu bạn thấy dễ hơn, bạn có thể để độ dài các cạnh dưới dạng số mũ, sau đó bình phương chúng sau.
- Trong ví dụ này, chúng ta sẽ bình phương 3 và 5 để được 9 và 25. Phương trình có thể được viết lại là 9 + b² = 25.
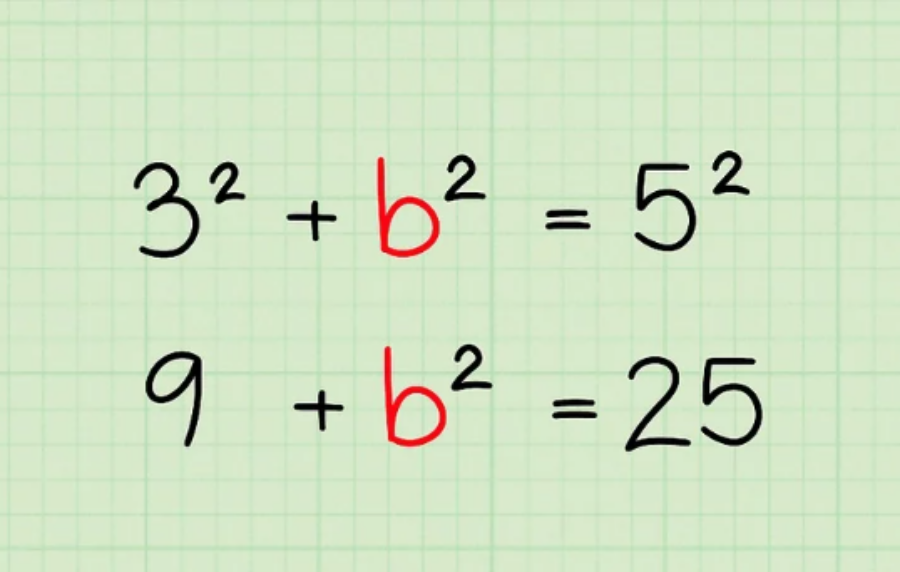
Bước 6: Tách biến chưa biết sang một vế của phương trình.
Nếu cần, bạn cũng nên sử dụng phép đại số cơ bản để đưa biến chưa biết sang 1 bên phương trình và 2 số bình phương sang 1 bên của phương trình. Nếu tìm cạnh huyền, c đã ở một vế riêng, do đó bạn không cần phải làm bất cứ điều gì để tách nó.
Ví dụ: Phương trình hiện tại là 9 + b² = 25. Để tách b², hãy trừ cả 2 vế phương trình cho 9. Phương trình có được là b² = 16.
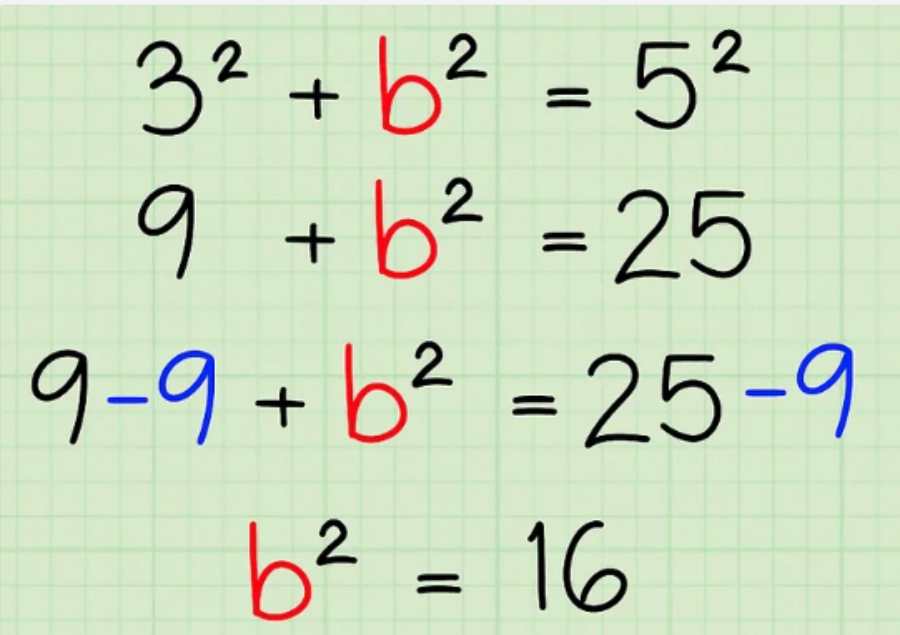
Bước 7: Lấy căn bậc hai của cả hai vế phương trình.
Khi còn lại 1 biến bình phương ở một vế của phương trình và một số ở vế kia. Đơn giản chỉ cần lấy căn bậc hai của cả hai vế để tìm độ dài cạnh chưa biết.
Ví dụ: b² = 16, lấy căn bậc hai của cả hai vế ta được b = 4 => chiều dài của cạnh cần tìm là 4.
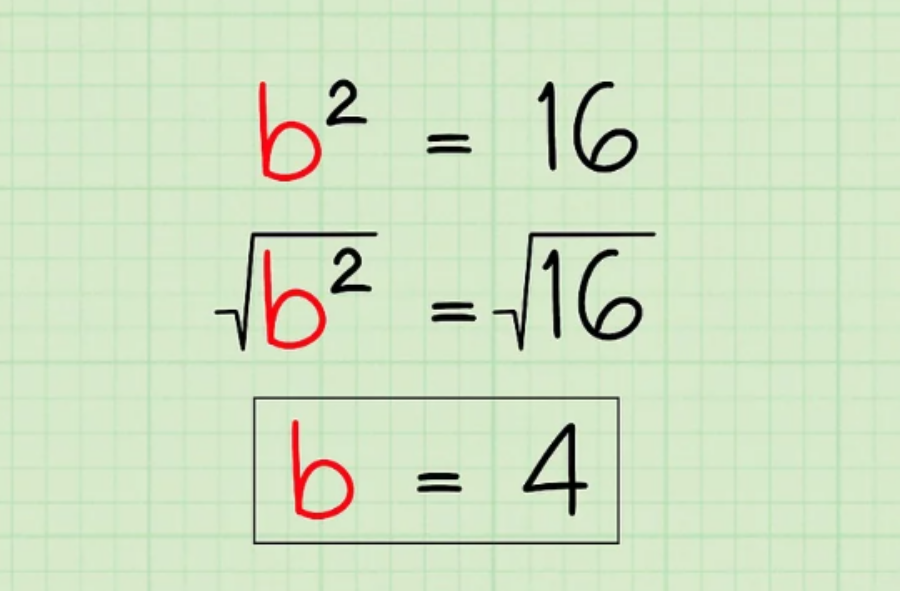
Bước 8: Sử dụng Định lý Pytago để tìm cạnh của tam giác vuông trong thực tế.
Bất cứ trường hợp nào mà hai vật hoặc hai đường thẳng giao nhau tại một góc vuông và vật hoặc đường thẳng thứ ba cắt chéo qua góc vuông đó thì bạn đều có thể sử dụng Định lý Pytago để tìm độ dài của một trong các cạnh khi biết chiều dài của hai cạnh còn lại.
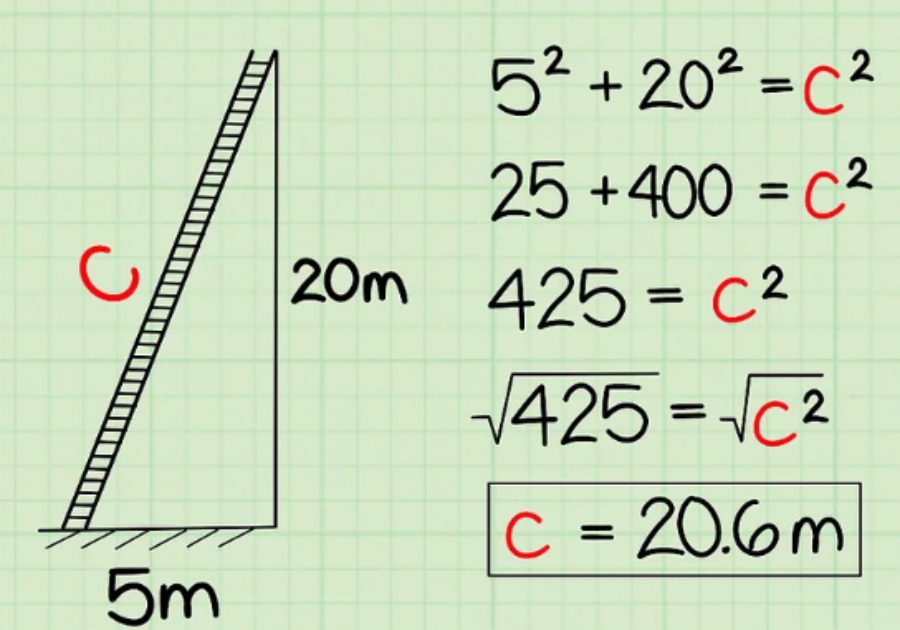
Ví dụ: Một chiếc thang đang đứng dựa vào tòa nhà. Đáy thang cách chân tường 5m. Thang cao tới 20m của tòa nhà. Hỏi thang dài bao nhiêu m?
Giải: Đáy thang cách chân tường 5 m và cao 20 m của bức tường tòa nhà cho bạn biết chiều dài 2 cạnh của tam giác. Bởi vì bức tường và mặt đất giao nhau tại 1 góc vuông và chiếc thang dựng vào bước tường theo đường chéo, bạn có thể hình dung nó như 1 tam giác vuông với chiều dài cạnh a = 5 và b = 20. Chiếc thang là cạnh huyền, vậy c chưa biết. Hãy sử dụng Định lý Pytago:
- a² + b² = c²
- (5)² + (20)² = c²
- 25 + 400 = c²
- 425 = c²
- Căn bậc hai của (425) = c
- c = 20,6. Chiều dài chiếc thang xấp xỉ là 20,6 m.
2. Tính Khoảng cách giữa hai điểm trong mặt phẳng X-Y
Bước 1: Xác định hai điểm trong mặt phẳng X-Y.
Định lý Pytago có thể dùng để tính khoảng cách đường thẳng giữa 2 điểm trong mặt phẳng X-Y. Nên bạn chỉ cần biết là tọa độ x và y của hai điểm bất kỳ. Thường thì những tọa độ này được viết theo cặp thứ tự tọa độ là (x, y).
Bên cạnh đó, để tìm khoảng cách giữa 2 điểm này, bạn sẽ coi mỗi điểm là 1 trong những góc nhọn của tam giác vuông.
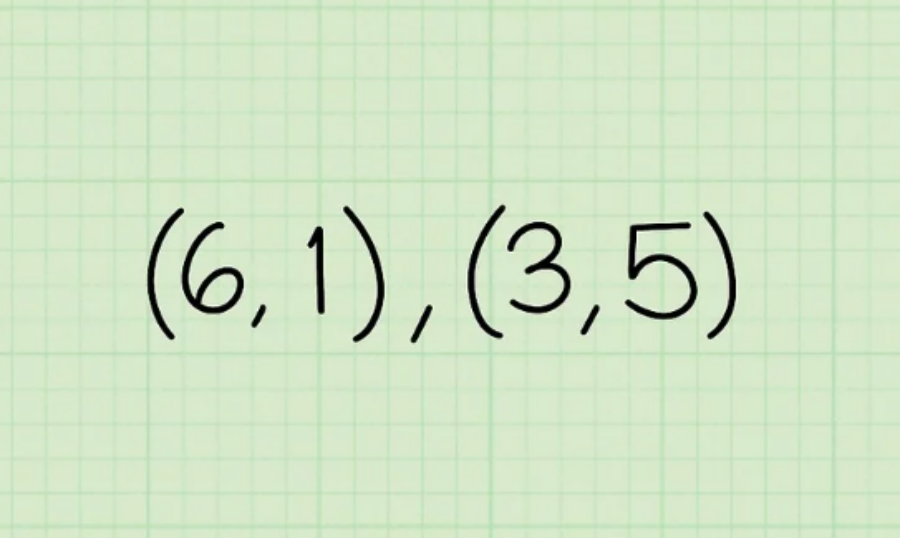
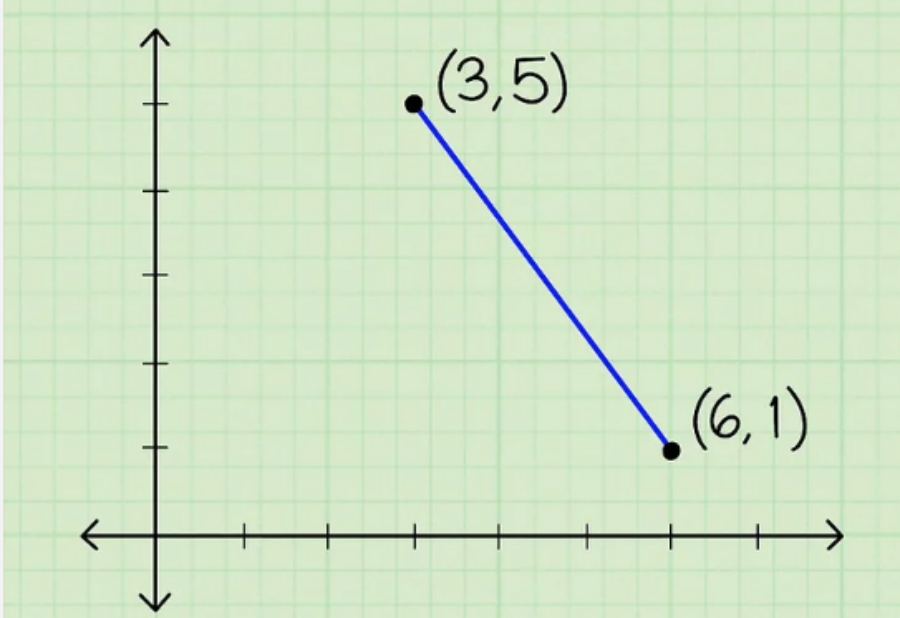
Bước 2: Vẽ hai điểm trên đồ thị.
Trong mặt phẳng X-Y, với mỗi điểm (x, y), x là tọa độ trên trục hoành và y là tọa độ trên trục tung. Bạn có thể dễ dàng tìm khoảng cách giữa 2 điểm mà không cần vẽ chúng trên đồ thị, nhưng vẽ đồ thị sẽ giúp bạn nhìn rõ hơn.
Bước 3: Tìm chiều dài các cạnh góc vuông của tam giác.
Tiếp theo, bạn nên sử dụng 2 điểm đã cho như các góc của tam giác liền kề với cạnh huyền, tìm độ dài cạnh a và b của tam giác. Thể hiện 1 cách trực quan trên đồ thị, hoặc bằng cách sử dụng công thức |x1 – x2| cho cạnh nằm ngang và |y1 – y2| cho cạnh thẳng đứng, trong đó (x1,y1) là điểm đầu tiên và (x2,y2) là điểm thứ 2.
Giả sử hai điểm là (6,1) and (3,5). Chiều dài cạnh nằm ngang của tam giác là:
- |x1 – x2|
- |3 – 6|
- | -3 | = 3
Chiều dài cạnh thẳng đứng là:
- |y1 – y2|
- |1 – 5|
- | -4 | = 4
Vậy, chúng ta có thể nói rằng trong tam giác vuông này, cạnh a = 3 và cạnh b = 4.
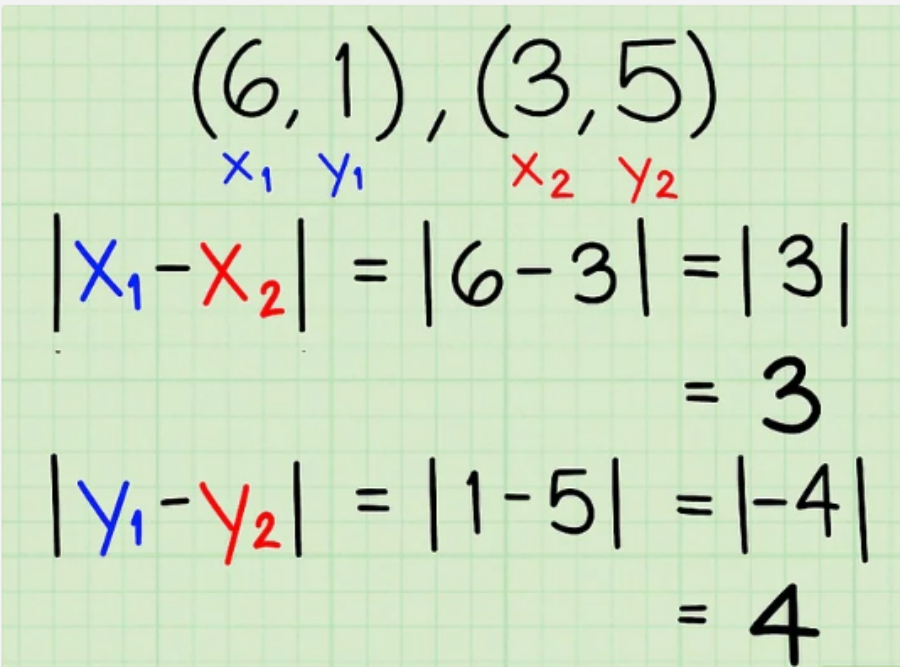
Bước 4: Sử dụng Định lý Pytago để giải phương trình tìm cạnh huyền.
Bởi vì khoảng cách giữa 2 điểm đã cho là cạnh huyền của tam giác có 2 cạnh góc vuông. Do đó, bạn dùng Định lý Pytago để tìm cạnh huyền, đặt a là chiều dài cạnh thứ nhất và b là chiều dài cạnh thứ hai.
Trong ví dụ với các điểm là (3,5) và (6,1), chiều dài các cạnh góc vuông là 3 và 4, do đó chúng ta tính chiều dài cạnh huyền như sau:
- (3)²+(4)²= c²
- c= căn bậc hai của (9+16)
- c= căn bậc hai của (25)
- c= 5. Khoảng cách giữa hai điểm (3,5) và (6,1) là 5

Những điều cần lưu ý khi học định lý Pitago
Trong quá trình học định lý Py-ta-go,bạn cần nắm vững kiến thức và đặc biệt chú ý đến những vấn đề sau:
- Trong thời gian tính toán, cần chú ý thật cẩn thận và nhìn đáp án xem đã chuẩn chưa.
- Nhìn vào hình, bạn cần nắm được đâu là cạnh góc vuông, đâu là cạnh huyền bởi đó là cạnh dài nhất đối diện góc lớn nhất, còn cạnh nào ngắn nhất sẽ đối diện với góc nhỏ nhất trong tam giác.
- Thường cạnh huyền của tam giác vuông sẽ cắt ngang qua góc vuông mà không đi qua góc vuông đó. Đây là cạnh dài nhất trong tam giác vuông và được gọi là C trong định lý Pytago.
- Cần phải tìm được độ dài hai cạnh còn lại trong tam giác vuông thì mới có thể tính được cạnh thứ 3.
- Trong một hình tam giác ngoài trường hợp tam giác vuông thì bạn không thể áp dụng định lý Pitago.
- Nếu chỉ biết chiều dài của một cạnh thì bạn cũng không thể áp dụng định lý Pitago.
Một số bài tập vận dụng định lý Pytago
1. Bài tập vận dụng định lý Pytago có lời giải
Câu 1: Cho tam giác ABC có AC = 5 cm, BC = 3 cm, AB = 4 cm. Tam giác ABC là tam giác gì?
Giải:
Ta có : AC² = BC² + AB² ( vì 5² = 3 ² + 4² )
Nên tam giác ABC vuông tại B ( định lý Pytago đảo ).
Câu 2: Tìm độ dài x trên hình sau:
Giải: Áp dụng định lý Pytago, ta có:
Tam giác ABC vuông tại B
=> x² + 8² = 10²
=> x² = 10² -8² = 6² = 36
=> x = 6 (cm)
Câu 3: Tính chiều dài cạnh huyền của các tam giác sau, biết:
a. Tam giác MNO vuông tại M có cạnh MO = 4 cm, cạnh MN = 5 cm
b. Tam giác PQR vuông tại P có cạnh PQ = 7 cm, cạnh PR = 6 cm
c. Tam giác BCD vuông tại B có cạnh BC = 8 cm, cạnh BD = 2 cm
d. Tam giác IKL vuông tại I có cạnh IL = 4,5 cm, cnahj IK = 8 cm
Giải:
a. Vì tam giác MNO vuông tại M, NO là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:
NO2 = MN2 + MO2
=> NO2 = 42 + 52
=> NO2 = 41
=> NO = √41
=> NO = 6,4
Vậy chiều dài cạnh NO của tam giác MNO là 6,4 cm
Vì tam giác PQR vuông tại P, QR là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:
QR2 = PQ2 + PR2
=> QR2 = 72 + 62
=> QR2 = 85
=> QR = √85
=> QR = 9,2
Vậy chiều dài cạnh QR của tam giác PQR là 9,2 cm
c. Vì tam giác BCD vuông tại B, CD là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:
CD2 = BC2 + BD2
=> CD2 = 82 + 22
=> CD2 = 70
=> CD = √70
=> CD = 8,4
Vậy chiều dài cạnh CD của tam giác BCD là 8,4 cm
d. Vì tam giác IKL vuông tại I, KL là cạnh góc vuông, do đó, ta áp dụng định lý Pytago trong tam giác vuông:
KL2 = IL2 + IK2
=> KL2 = 4,52 + 82
=> KL2 = 84,25
=>KL = √84,25
=> KL = 9,2
Vậy chiều dài cạnh CD của tam giác BCD là 9,2 cm
Câu 4: Xét tam giác ABC vuông tại A:
a. Biết chiều dài cạnh AB = 4 cm, chiều dài cạnh BC = 6 cm, tính chiều dài cạnh AC
b. Biết chiều dài cạnh AC = 2 cm, chiều dài cạnh BC = 7 cm, tính chiều dài cạnh AB
c. Biết chiều dài cạnh AB = 3 cm, chiều dài cạnh AC = 5 cm, tính chiều dài cạnh BC
Giải:
a. Ta có : BC2 = AC2 + AB2
=> AC2 = BC2 – AB2
=> AC2 = 6² – 4²
=> AC = căn bậc hai của 20 ( cm ).
b. Ta có: BC2 = AC2 + AB2
=> AB2 = BC2 – AC2
=> AB2 = 7² – 2²
=> AB = căn bậc hai của 45 ( cm ).
c. Ta có : BC2 = AC2 + AB2
=> BC2 = 3² + 5²
=> BC = căn bậc hai của 34 ( cm )
Câu 5: Tính chiều cao của bức tường, biết rằng chiều dài của thang là 4m và chân thang cách tường là 1m
Giải:
Vì mặt đất vuông góc với chân tường nên góc C = 90 độ
Áp dụng định lý Pytago trong tam giác vuông ABC ( vuông tại C ) , ta có:
AC ^ 2 + BC ^ 2 = AB ^ 2
=> AC ^ 2 = AB ^ 2 – BC ^ 2 = 4 ^ 2 – 1 ^ 2 = 16 – 1 = 15
=> AC = căn bậc hai của 15 ( m ) ~ 3,87 ( m ).
Do vậy, chiều cao của bức tường là 3,87 m.
Toán 7 Tập 1 Bài 7 trang 130: Vẽ tam giác ABC có AB = 3cm; AC = 4cm; BC = 5cm. Hãy dùng thước đo góc để xác định số đo của góc BAC
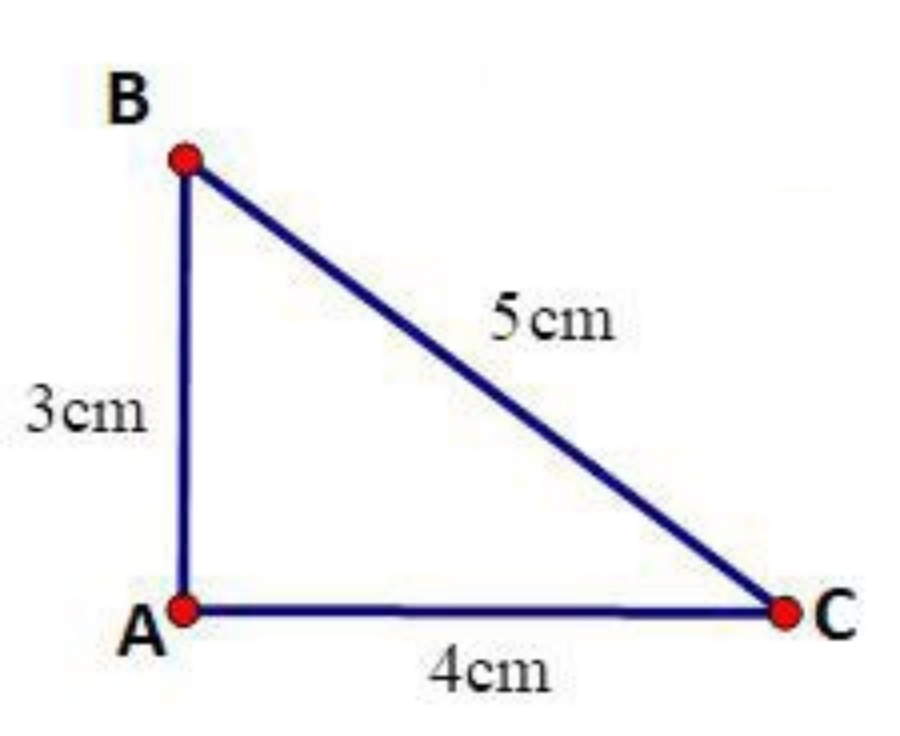
Giải: Số đo góc BAC là 90°
Bài 53 (trang 131 SGK Toán 7 Tập 1): Tìm độ dài x trên hình 127.
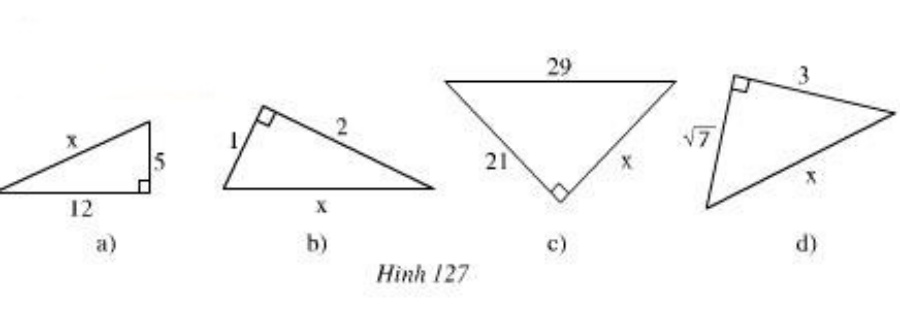
Giải: a) Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 => x = 13
b) Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
=> x = √5
c) Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 – 212 = 841 – 441 = 400
=> x = 20
d) Hình d
Theo định lí Pi-ta-go: 7 + 32 = x2
=> x2 = 16 => x = 4
Bài 54 (trang 131 SGK Toán 7 Tập 1): Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.
Giải:
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AB2 + BC2 = AC2
=> AB2 = AC2 – BC2 = 8,52 – 7,52
= 72,25 – 56,25 = 16
Vậy AB = 4(cm)
Bài 56 (trang 131 SGK Toán 7 Tập 1): Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau.
a) 9cm, 15cm, 12cm.
b) 5dm, 13dm, 12dm.
c) 7m, 7m, 10m.
Giải: a) Ta có: 152= 225 = 92+ 122 = 81 + 144
Nên tam giác có độ dài 9cm, 12cm, 15cm là tam giác vuông
b) Tương tự là tam giác vuông (vì 52+ 122= 132)
c) Không là tam giác vuông (vì 72+ 72< 102)
2. Bài tập vận dụng định lý Pytago không có lời giải
Câu 1: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2dm
A. BC = 4dm
B. BC = √6dm
C. BC = 8dm
D. BC = √8 dm
Câu 2: Cho tam giác nhọn ABC, kẻ AH vuông góc với BC ( H ∈ BC). CHo biết AH=12cm, BH=5cm và BC=14cm. Tính các độ dài AB và AC.
A. AB= 14cm; AC= 15cm
B. AB= 13cm; AC= 15cm
C. AB= 15cm, AC= 16cm
D. Một kết quả khác với ba kết quả trên
Câu 3: Cho tam giác ABC vuông tại B BC=12cm, AC=13cm. Tính AB
A. x = 10cm
B. x = 11cm
C. x = 8cm
D. x = 5cm
Câu 4: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm
B. 10 cm, 24 cm
C. 12 cm, 24 cm
D. 15 cm, 24 cm
Câu 5: Cho tam giác MNP vuông tại M, MN=4,5cm, NP =7,5cm. TInh độ dài MP
A. 5,5cm
B. 7,5cm
C. 4,5cm
D. 6cm
Câu 6: Cho tam giác ABC vuông tại A. Kẻ AD ⊥ BC tại D. Biết AB = 7 cm, BD = 4 cm. Khi đó AD có độ dài là:
A. AD = 33 cm
B. AD = 3 cm
C. AD = √33 cm
D. AD = √3 cm
Câu 7: Một tam giác vuông có tỉ số hai cạnh góc vuông là 3 : 4 và chu vi tam giác đó là 36 cm. Tính cạnh huyền của tam giác đó.
A. 12 cm
B. 15 cm
C. 9 cm
D. 36 cm
Câu 8: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 15 cm; 8 cm; 18 cm
B. 21 cm; 20 cm; 29 cm
C. 5 cm; 6 cm; 8 cm
D. 2 cm; 3 cm; 4 cm
Câu 9: Tính chiều cao của bức tường, biết rằng chiều dài của thang là 7m và chân thang cách tường là 3m
Câu 10: Cho tam giác ABC có AC = 6 cm, BC = 4cm, AB = 2 cm. Tam giác ABC là tam giác gì?
Trên đây là Định lý Pytago và công thức tính định lý Pytago mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể áp dụng định lý Pytago để tính toán một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn đạt được điểm số cao.
Tags:
công thức định lý pytagođịnh lý pytago trong tam giác vuôngcông thức định lý pytago đảo

