Là một trong những dạng kiến thức toán học phổ biến, Bất đẳng thức Côsi được sử dụng để giải nhiều dạng phương trình, bất phương trình khác nhau. Vậy bất đẳng thức Cosi là gì và nó được sử dụng như thế nào?
Đừng lo lắng, đội ĐẢO NGƯỢC Chúng tôi sẽ hướng dẫn các bạn bất đẳng thức Cosi là gì & cách sử dụng nó một cách chi tiết, dễ hiểu qua bài viết dưới đây.
Mục lục bài viết [Ẩn]

I. Thế nào là bất đẳng thức Côsi?
bất đẳng thức cosic hay bất đẳng thức AM-GM là một khái niệm toán học được sử dụng trong các bài toán phổ thông. Trong toán học, bất đẳng thức Côsi là bất đẳng thức so sánh trung bình cộng và trung bình nhân của n số thực không âm (TB cộng với các số thực không âm luôn > hoặc = TB nhân với chúng). Trường hợp n bằng nhau thì TB cộng = TB nhân.
Thực ra có nhiều cách chứng minh bất đẳng thức này nhưng cách tốt nhất vẫn là chứng minh theo quy nạp Cauchy.
1. AM – GM . bất bình đẳng

2. Bất đẳng thức cosic
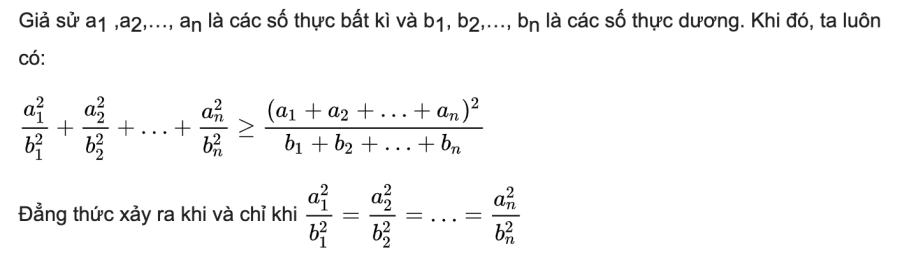
3. Bất đẳng thức cos đối với 2 số không âm
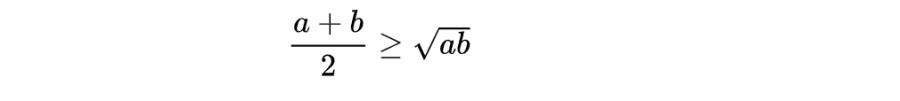
Dấu bằng xảy ra khi và chỉ khi a = b
4. Bất đẳng thức Côsi cho 3 số không âm
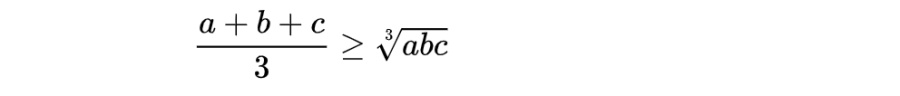
Dấu bằng xảy ra khi và chỉ khi a = b = c
5. Bất đẳng thức Côsi cho 4 số không âm
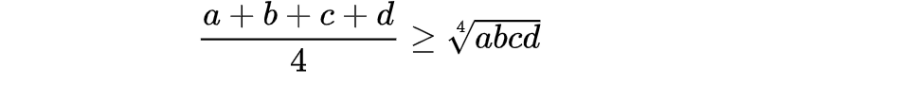
Dấu bằng xảy ra khi và chỉ khi a = b = c = d
6. Bất đẳng thức cos đối với n số không âm
Với xĐầu tiênx2…, xN là n số thực không âm thì ta có:
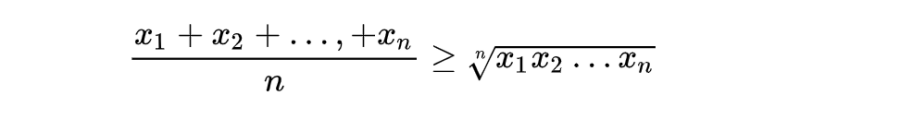
Đẳng thức xảy ra khi và chỉ khi xĐầu tiên = x2 =… = xN
* Hệ quả của bất đẳng thức Côsin
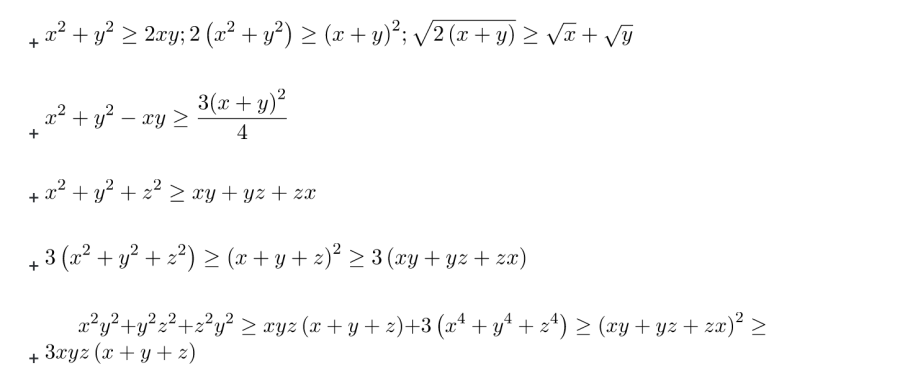
II. Chứng minh bất đẳng thức Côsi

1. Chứng minh bất đẳng thức Côsi nghiệm đúng với 2 số thực không âm
Với a = 0 và b = 0 thì bất đẳng thức luôn đúng (1). Ta chỉ cần chứng minh rằng bất đẳng thức luôn đúng với hai số dương a và b.

2. Chứng minh bất đẳng thức Côsi với 3 số thực không âm
Rõ ràng a = 0, b = 0, c = 0 thì bất đẳng thức luôn đúng. Do đó ta chỉ cần chứng minh bất đẳng thức đúng với 3 số thực dương a, b, c.
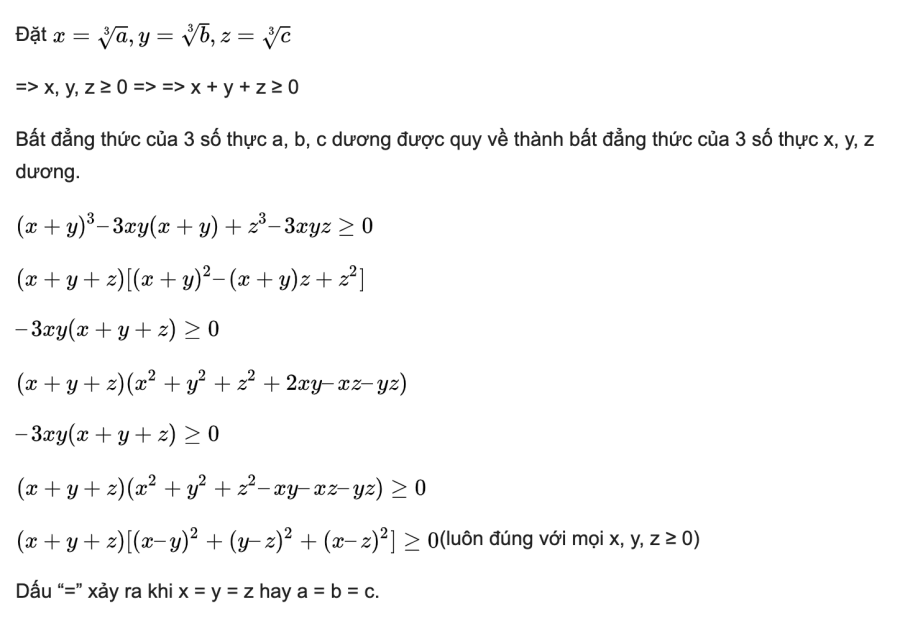
3. Chứng minh bất đẳng thức Côsi với 4 số thực không âm
Dễ thấy với a = 0, b = 0, c = 0, d = 0 thì bất đẳng thức luôn đúng. Bây giờ ta chỉ cần chứng minh bất đẳng thức đúng với 4 số thực dương.
Từ kết quả chứng minh bất đẳng thức đúng với 2 số thực không âm, ta có:

4. Chứng minh bất đẳng thức Côsi cho n số thực không âm
Theo chứng minh trên, n = 2 thì bất đẳng thức luôn đúng.
Nếu bất đẳng thức đúng với n số thì nó cũng đúng với 2n số. Chứng minh điều này như sau:
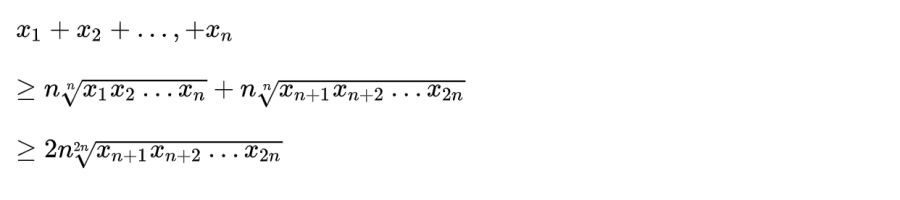
Bằng quy nạp, bất đẳng thức đúng với n là lũy thừa của 2.
Mặt khác, giả sử bất đẳng thức đúng với n số, ta cũng có thể chứng minh nó đúng với n-1 số như sau:
Theo bất đẳng thức cos đối với n số:
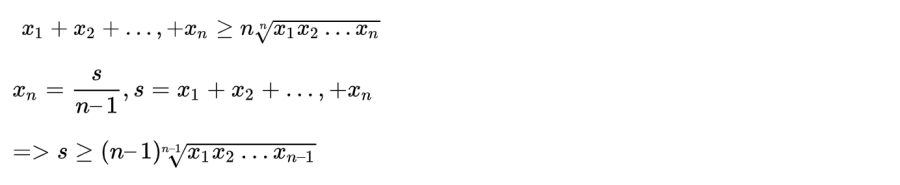
Đây là số Cosi(n-1). Vì vậy, chúng tôi có dpcm.
III. Một số bài tập về bất đẳng thức Cosi
1. Bài tập vận dụng bất đẳng thức Côsi có lời giải
Bài toán 1: Tìm giá trị nhỏ nhất của biểu thức:
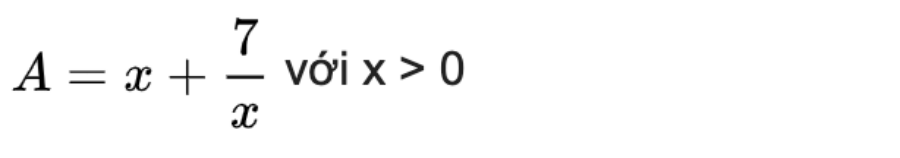
Phần thưởng
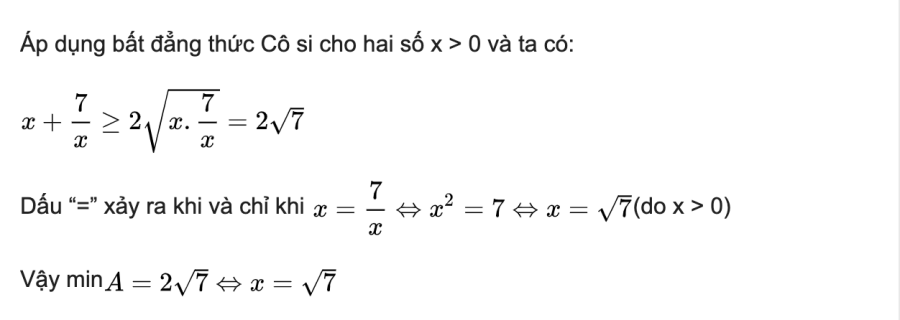
Bài toán 2: Cho các số thực dương a, b, c thỏa mãn
![]()
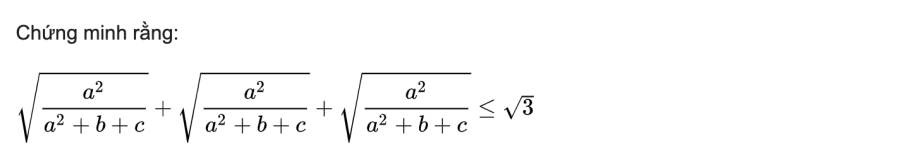
Phần thưởng
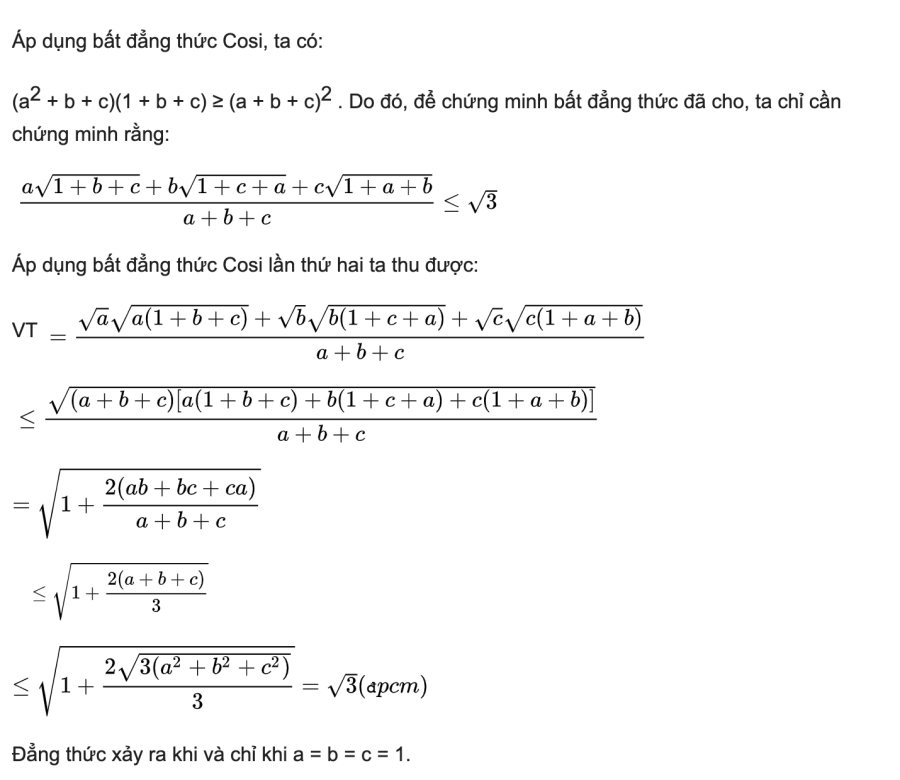
Bài 3: Cho x > 0, y > 0 thỏa mãn điều kiện

![]()
Phần thưởng
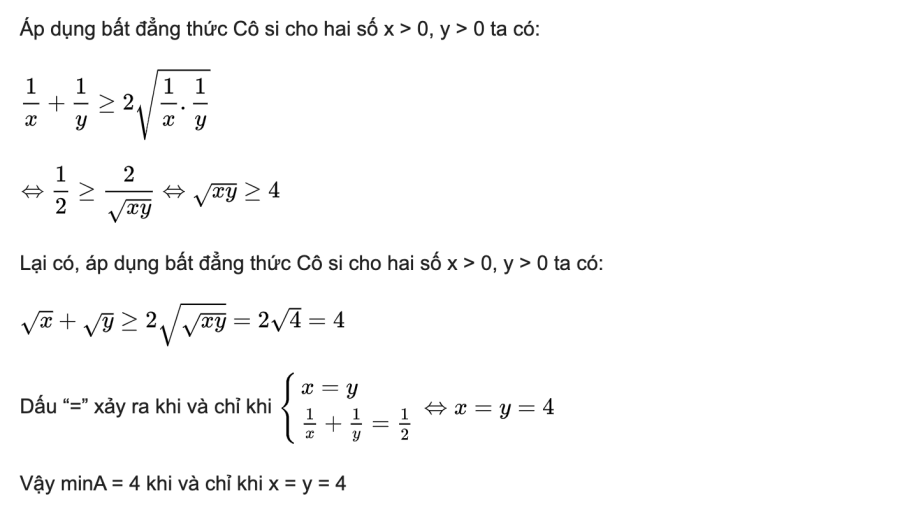
Chủ đề 4:
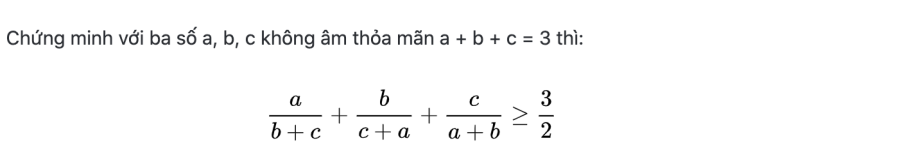
Phần thưởng

Chủ đề 5:
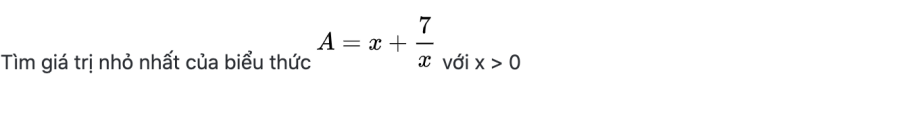
Phần thưởng
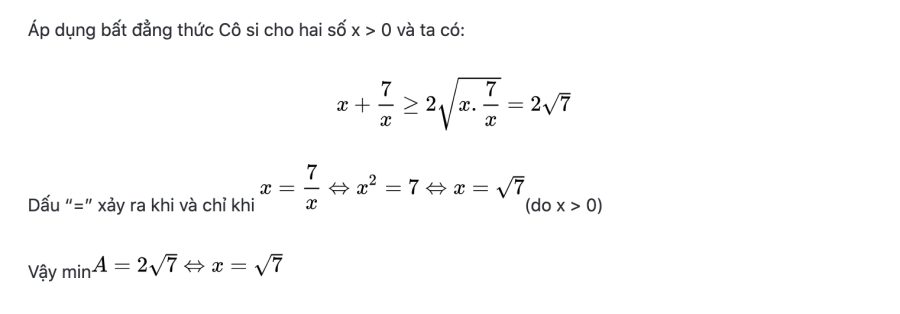
2. Bài tập áp dụng bất đẳng thức Côsi vô nghiệm
Bài toán 1: Giải phương trình sau:
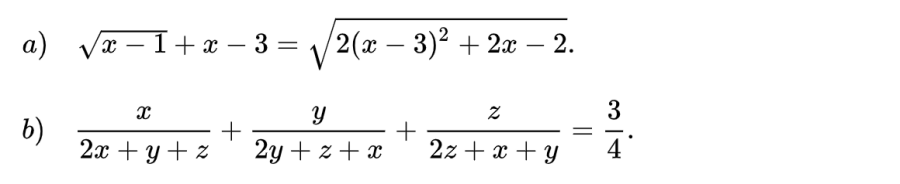
Bài toán 2: Giải phương trình sau:
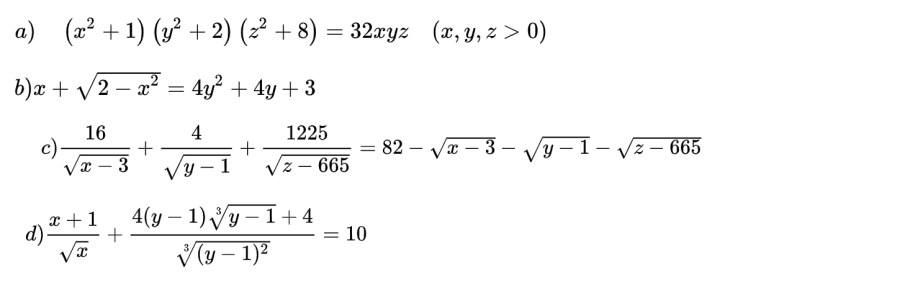
Bài 3: Giải hệ phương trình sau:

Bài 4: Giải hệ phương trình
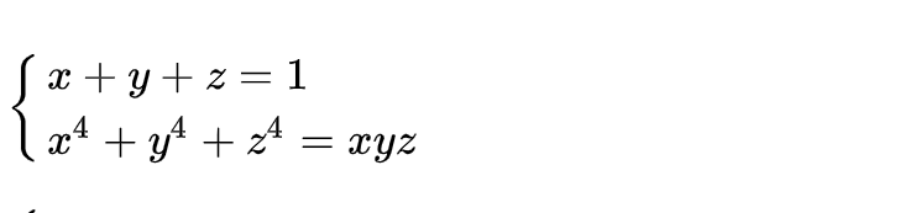
Bài 5: Giải hệ phương trình
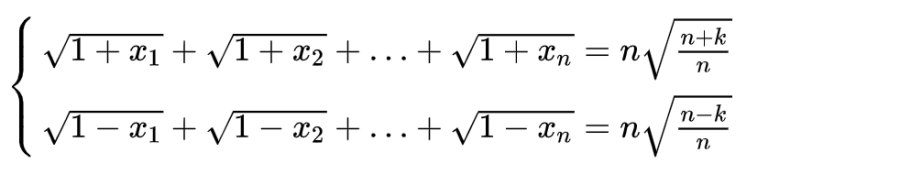
Bài 6: Xác định số nguyên dương n và các số dương x1, x2,…,xn thỏa mãn:

Bài 7: Cho ba số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh rằng:

(đề nghị dùng phương pháp trội)
Bài 8: Tìm giá trị nhỏ nhất của các biểu thức sau:
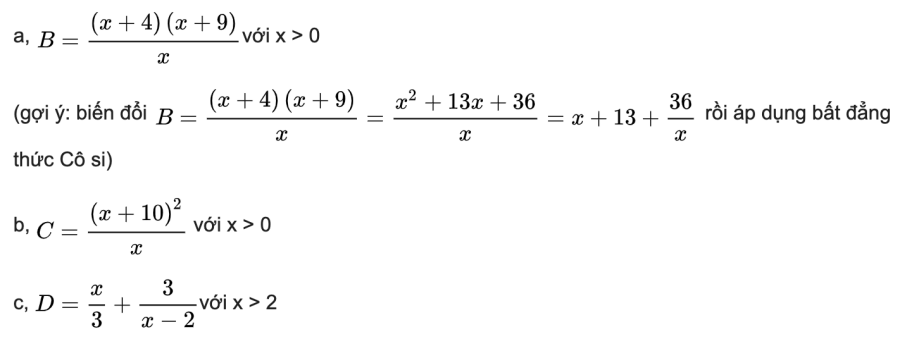
(gợi ý: biến đổi rồi áp dụng bất đẳng thức Cosi)
Bài 9: Tìm giá trị nhỏ nhất của biểu thức
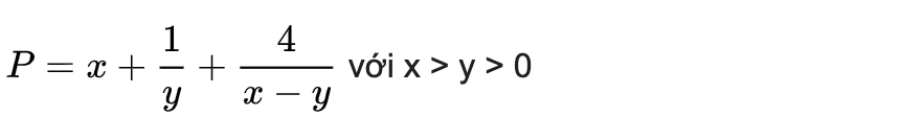
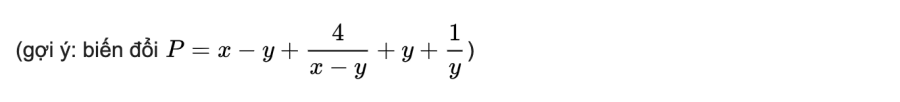
Trên đây là Bất đẳng thức Côsi và bài tập ứng dụng mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này các bạn đã có thể hoàn toàn biết được bất đẳng thức Côsi là gì cũng như vận dụng nó để giải bài toán một cách dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%

