1. Bài tập tổng hợp hình học lớp 8:
Câu 1. Tứ giác ABCD có A = 72º, B = 114º, D = 85º. Tính số đo góc C.
Câu 2. Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
B. Hình thang cân có hai cạnh bên bằng nhau.
C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.
D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Câu 3: Cho hình thang cân ABCD (như hình vẽ) có BAD = 60º. Số đo của BCD = ?
A. 50º
B. 60º
C. 120º
D. 80º
Câu 4. Cho hình thang cân ABCD (AB // CD) . Tìm mệnh đề sai?
A. tam giác ABC = tam giác BAD
B. góc CAB = góc DBA
C. tam giác ABE cân
D. tam giác AED cânư
Câu 5. Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD lần lượt tại H và tại K. Chứng minh tứ giác AHCK là hình bình hành.
Câu 6. Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
Câu 7. Cho tam giác ABC , gọi M, N và P lần lượt là trung điểm của AC; AB và BC. biết AB = BC. Hỏi tứ giác NMPB là hình gì?
A. Hình thoi
B. Hình bình hành
C. Hình chữ nhật
D. Hình thang
Câu 8. Cho hình vuông ABCD. Trên cạnh AD, DC lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh:
a) Hai tam giác ADF và BAE bằng nhau;
b) BE vuông góc với AF.
2. Cách giải bài tập tổng hợp hình học lớp 8:
Câu 1.
Áp dụng định lý tổng các góc của tứ giác bằng khi đó tứ giác ABCD có: A + B + C + D = 360º ⇒ C = 360º − ( A + B + D )
Thay số ta được: C = 360º − ( 72º + 114º + 85º ) ⇒ C = 89º
Câu 2.
Lời giải:
+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân. → Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau. → Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau. → Đáp án D đúng, đáp án C sai.
Câu 3.
Áp dụng tính chất của hình thang cân ta có: A = B ; C = D
Mà A + B + C + D = 360º ⇔ 2 A + 2 C = 360º ⇒ 2 C = 360º – 2 A = 360º – 2.60º = 240º ⇔ Cˆ = 120º
Chọn đáp án C.
Câu 4.
Xét tam giác ABC và tam giác BAD ta có: AD = BC (vì ABCD là hình thang cân) ; AB chung; AC = BD (hình thang cân có 2 đường chéo bằng nhau)
Suy ra: tam giác ABC = tam giác BAD (c.c.c) => góc CAB = góc DBA (hai góc tương ứng)
Hay góc EAB = góc EBA. Do đó, tam giác ABE cân tại E
Câu 5.
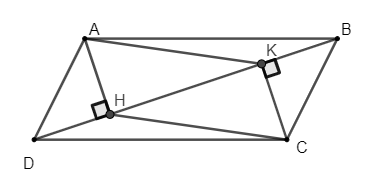
Vì tứ gác ABCD là hình bình hành: ⇒ { AD = BC; AD / / BC
Vì AD // BC nên ADH = CBK (hai góc so le trong)
Ta có: { AH ⊥ BD ; CK ⊥ BD ⇒ AHD = 90 ° ; CKB = 90 ° ; AH / / CK
Xét tam giác AHD và tam giác CKB có: AHD = CKB = 90 ° ; ADH = CBK; AD = BC ⇒ Δ AHD = Δ CKB (cạnh huyền – góc nhọn) ⇒ AH = CK (hai cạnh tương ứng)
Xét tứ giác AHCK có: { AH = CK; AH / / CK ⇒ tứ giác AHCK là hình bình hành (dấu hiệu nhận biết).
Câu 6.
.png)
Ta có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm tam giác ABC.
Theo tính chất trọng tâm tam giác ta có: { BG = 2 GM; CG = 2 GN (1)
Lại có: G đối xứng với với D qua M ⇒ GM = MD ⇒ GD = 2GM (2)
G đối xứng với E qua N ⇒ GN = EN ⇒ GE = 2GN (3)
Từ (1); (2); (3) ⇒ { BG = GD; CG = GE ⇒ G là trung điểm của BD; G là trung điểm CE
Xét tứ giác BCDE có: G là trung điểm của đường chéo BD; G là trung điểm đường chéo CE. Do đó: tứ giác BCDE là hình bình hành.
Lại có: Δ ABC cân tại A nên AB = AC. Mà M là trung điểm của AC, N là trung điểm AB nên BN = CM
Xét tam giác BNC và tam giác CMB có: BC chung; BN = CM ; NBC = MCB (do tam giác ABC cân tại A) Do đó: Δ BNC = Δ CMB (c – g –c) ⇒ CN = BM (hai cạnh tương ứng)
Mà { CN = 3/4 EC; BM = 3/4 BD
Do đó EC = BD. Xét hình bình hành BCDE có hai đường chép EC và BD bằng nhau ⇒ Hình bình hành BCDE là hình chữ nhật (dấu hiệu nhận biết).
Câu 7.
Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và MN = 1/2 BC (1)
Lại có: P là trung điểm của BC nên BP = 1/2 BC (2)
Từ (1) và (2) suy ra: MN = BP. Tứ giác NMPB có 2 cạnh đối MN và BP song song và bằng nhau nên là hình bình hành.
Lại có: N là trung điểm của AB nên BN = 1/2 AB
Theo giả thiết AB = BC nên từ (1) và (2) suy ra: BP = BN
Hình bình hành NMPB có 2 cạnh kề BP và BN bằng nhau nên là hình thoi.
Đáp án đúng là A.
Câu 8.
.png)
a) Vì ABCD là hình vuông nên AB = AD và D = EAB = 90 °
Xét hai tam giác ADF và BAE ta có: AD = AB ; D = EAB = 90 ° ; AE = DF ( giả thiết)
Do đó: Δ ADF = Δ BAE (c – g – c)
b) Gọi giao điểm của BE và AF là G.
Ta có: DFA + DAF = 90 °
Mà DFA = AEB (hai góc tương ứng của hai tam giác bằng nhau Δ ADF = Δ BAE ) Nên AEB + DAF = 90 ° hay A E G + E A G = 90 °
Mà theo định lý tổng ba góc trong tam giác AEG ta có: AGE + AEG + EAG = 180 ° ⇒ AGE + 90 ° = 180 ° ⇒ AGE = 90 ° ⇒ BE ⊥ AF tại G.
3. Tổng quát chương trình hình học lớp 8:
Chương 3: Tứ giác
Bài 10: Tứ giác: Sử dụng tính chất về các góc của một tứ giác để tính góc; Sử dụng bất đẳng thức tam giác để giải các bài toán liên hệ đến các cạnh của một tứ giác
Bài 11: Hình thang cân: Tính chất các góc của một hình thang; Sử dụng tính chất của hình thang cân để tính toán và chứng minh; Chứng minh một tứ giác là hình thang cân
Bài 12: Hình bình hành: Vận dụng tính chất của hình bình hành để chứng minh tính chất hình học; Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành
Bài 13: Hình chữ nhật: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình chữ nhật; Vận dụng kiến thức hình chữ nhật để giải toán
Bài 14: Hình thoi và hình vuông: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi; Vận dụng kiến thức hình thoi để giải toán; Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông; Vận dụng kiến thức hình vuông để giải toán
Chương 4: Định lí Talet
Bài 15: Định lí Talet trong tam giác: Tính độ dài đoạn thẳng; Chứng minh hai đường thẳng song song
Bài 16: Đường trung bình của tam giác
Bài 17: Tính chất đường phân giác của tam giác
Chương 9: Tam giác đồng dạng: Sử dụng tam giác đồng dạng để tính toán
Bài 33: Hai tam giác đồng dạng: Chứng minh hai tam giác đồng dạng
Bài 34: Ba trường
Bài 35: Định lí Pythagore và ứng dụng
Bài 36: Các trường hợp đồng dạng của hai tam giác vuông
Bài 37: Hình đồng dạng
Chương 10: Một số hình khối trong
Bài 38: Hình chóp tam giác đều
Bài 39: Hình chóp tứ giác đều

