Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 7

Bạn đang xem: Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 7 tại truongptdtntthptdienbiendong.edu.vn

1. Đề số 1:

Bài 1: (3 điểm): Tính

$left[ {18frac{1}{6} - left( {0,06:7frac{1}{2} + 3frac{2}{5}.0,38} right)} right]:left( {19 - 2frac{2}{3}.4frac{3}{4}} right)$

Bài 2: (4 điểm) Cho $frac{a}{c} = frac{c}{b}$ chứng minh rằng:

a. $frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = frac{a}{b}$

b. $frac{{{b^2} - {a^2}}}{{{a^2} + {c^2}}} = frac{{b - a}}{a}$

Bài 3: (4 điểm): Tìm x biết:

a. $left| {x + frac{1}{5}} right| - 4 = - 2$

b. $- frac{{15}}{{12}}x + frac{3}{7} = frac{6}{5}x - frac{1}{2}$

Bài 4: (3 điểm) Một vật chuyển động trên các cạnh hình vuông. Trên hai cạnh đầu vật chuyển động với vận tốc 5m/s, trên cạnh thứ ba với vận tốc 4m/s, trên cạnh thứ tư với vận tốc 3m/s. Hỏi độ dài cạnh hình vuông biết rằng tổng thời gian vật chuyển động trên bốn cạnh là 59 giây.

Bài 5: (4 điểm) Cho tam giác ABC cân tại A có A = 20⁰, vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân giá của góc ABD cắt AC tại M. Chứng minh:

a) Tia AD là phân giác của góc BAC

b) AM = BC

Bài 6: (2 điểm): Tìm x , y ∈ N biết: 25 – y ² = 8( x – 2009)²

ĐÁP ÁN:

Bài 1.

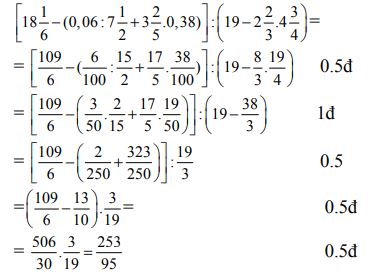
30 đề thi HSG Toán 7 có đáp án

Bài 2

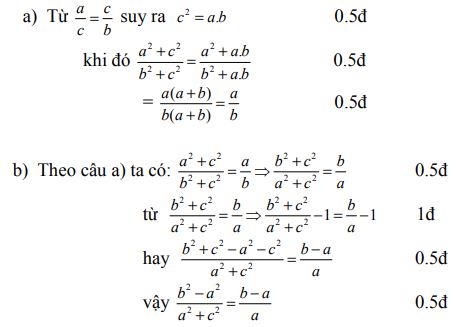
30 đề thi HSG Toán 7 có đáp án

Bài 3

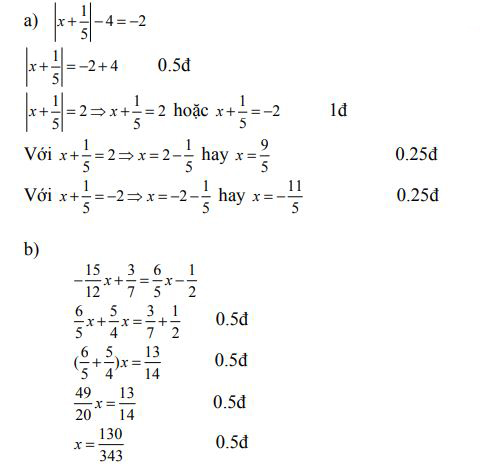
30 đề thi HSG Toán 7 có đáp án

Bài 4

Cùng một đoạn đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Gọi x, y, z là thời gian chuyển động lần lượt với các vận tốc 5m/s; 4m/s; 3m/s.

Ta có: 5x = 4y = 3z và x + y + z = 59

Hay $dfrac{x}{{dfrac{1}{5}}} = dfrac{y}{{dfrac{1}{4}}} = frac{z}{{dfrac{1}{3}}} = dfrac{{x + y + z}}{{dfrac{1}{5} + dfrac{1}{4} + dfrac{1}{3}}} = dfrac{{59}}{{dfrac{{59}}{{60}}}} = 60$

Do đó: x = 60. $frac{1}{5}$ = 12

y = 60. $frac{1}{4}$ = 15

z = 60. $frac{1}{3}$ = 20

Vậy cạnh hình vuông là 5.12 = 60m

Bài 5

Vẽ hình, ghi GT, KL đúng 0,5đ

a. Chứng minh ΔADB = ΔADC (c – c – c) 1đ

Suy ra $widehat {DAB} = widehat {DAC}$

Do đó: $widehat {DAB}$ = 20⁰ : 2 = 10⁰

b. Ta có: ΔABC cân tại A, mà $widehat A$ = 20⁰ (gt) nên $widehat {ABC}$ = (180⁰ – 20⁰) : 2 = 80⁰

ΔABC đều nên $widehat {DBC}$ = 60⁰

Tia BD nằm giữa hai tia BA và BC suy ra $widehat {ABD}$ = 80⁰ – 60⁰ = 20⁰

Tia BM là tia phân giác của góc ABD nên $widehat {ABM}$ = 10⁰

Xét ΔABM và ΔBAD ta có:

AB là cạnh chung

$begin{gathered} widehat {BAM} = widehat {ABD} = {20^0} hfill \ widehat {ABM} = widehat {DAB} = {10^0} hfill \ end{gathered}$

Vậy ΔABM = ΔBAD (g – c – g)

Suy ra AM = BD, mà BD = BC (gt) nên AM = BC

Bài 6

25 – y² = 8(x – 2009)²

Ta có: 8(x – 2009)² = 25 – y²

8(x – 2009)² + y2 = 25 (*)

Vì y² ≥ 0 nên (x – 2009)² ≤ $dfrac{25}{8}$ ⇒ (x- 2009)² = 0 hoặc (x – 2009)² = 1

Với (x – 2009)² = 0 thay vào (*) ta được y² = 17 (loại)

Với (x – 2009)² = 1 thay vào (*) ta có y² = 25 suy ra y = 5 (do y ∈ $mathbb{N}$ )

Từ đó tìm được x = 2009; y = 5

2. Đề số 2:

Câu 1: Với mọi số tự nhiên n ≥ 2 hãy so sánh:

a. $A = frac{1}{{{2^2}}} + frac{1}{{{3^2}}} + frac{1}{{{4^2}}} + ... + frac{1}{{{n^2}}}$ với 1

b. $B = frac{1}{{{2^2}}} + frac{1}{{{4^2}}} + frac{1}{{{6^2}}} + ... + frac{1}{{{{left( {2n} right)}^2}}}$ với 0,5

Câu 2: Tìm phần nguyên của α, với α = $sqrt 2 + sqrt[3]{{frac{3}{2}}} + sqrt[3]{{frac{4}{3}}} + ... + sqrt[{n + 1}]{{frac{{n + 1}}{n}}}$

Câu 3: Tìm tỉ lệ 3 cạnh của một tam giác, biết rằng cộng lần lượt độ dài hai đường cao của tam giác đó thì tỉ lệ các kết quả là 5: 7: 8.

Câu 4: Cho góc xOy, trên hai cạnh Ox và Oy lần lượt lấy các điểm A và B để cho AB có độ dài nhỏ nhất.

Câu 5: Chứng minh rằng nếu a, b, c và $sqrt a + sqrt b + sqrt c$ là các số hữu tỉ.

ĐÁP ÁN:

Câu 1: (2 điểm)

Do $frac{1}{{{n^2}}} < frac{1}{{{n^2} - 1}}$ với mọi n ≥ 2 nên

A < C = $frac{1}{{{2^2} - 1}} + frac{1}{{{3^2} - 1}} + ... + frac{1}{{{n^2} - 1}}$

Mặt khác:

$begin{matrix} C = dfrac{1}{{1.3}} + dfrac{1}{{2.4}} + dfrac{1}{{3.5}} + ... + dfrac{1}{{left( {n - 1} right)left( {n + 1} right)}} hfill \ C = dfrac{1}{2}left( {dfrac{1}{1} - dfrac{1}{3} + dfrac{1}{2} - dfrac{1}{4} + dfrac{1}{3} - dfrac{1}{5} + ... + dfrac{1}{{n - 1}} - dfrac{1}{{n + 1}}} right) hfill \ C = - left( {1 + dfrac{1}{2} - dfrac{1}{n} - dfrac{1}{{n + 1}}} right) < dfrac{1}{2}.dfrac{3}{2} = dfrac{3}{4} < 1 hfill \ end{matrix}$

Vậy A < 1

b. (1 điểm)

$begin{matrix} B = dfrac{1}{{{2^2}}} + dfrac{1}{{{4^2}}} + ... + dfrac{1}{{{{left( {2n} right)}^2}}} hfill \ B = dfrac{1}{{{2^2}}}left( {1 + dfrac{1}{{{2^2}}} + dfrac{1}{{{3^2}}} + .... + dfrac{1}{{{n^2}}}} right) hfill \ B = dfrac{1}{{{2^2}}}left( {1 + A} right) hfill \ end{matrix}$

Suy ra P < 0,5

Câu 2 (2 điểm):

Ta có: $sqrt[{k + 1}]{{frac{{k + 1}}{k}}} > 1,left( {k = overline {1,n} } right)$

Áp dụng bất đẳng thức Cauchy cho k + 1 số ta có:

$begin{matrix} sqrt[{k + 1}]{{dfrac{{k + 1}}{k}}} = sqrt[{k + 1}]{{dfrac{{1 + 1 + .... + 1}}{k}dfrac{{k + 1}}{k}}} < dfrac{{1 + 1 + ... + 1 + dfrac{{k + 1}}{k}}}{{k + 1}} = dfrac{k}{{k + 1}} + dfrac{1}{k} = 1 + dfrac{1}{{kleft( {k + 1} right)}} hfill \ Rightarrow 1 < sqrt[{k + 1}]{{dfrac{{k + 1}}{k}}} < 1 + left( {dfrac{1}{k} - dfrac{1}{{k + 1}}} right) hfill \ end{matrix}$

Lần lượt cho k = 1, 2, 3, … rồi cộng lại ta được

$n < sqrt 2 + sqrt[3]{{frac{3}{2}}} + ... + sqrt[{n + 1}]{{frac{{n + 1}}{n}}} < n + 1 - frac{1}{n} < n + 1 Rightarrow left| alpha right| = n$

3. Các dạng toán nâng cao lớp 7:

Dạng 1: Tìm tổng của dãy số mà các số hạng cách đều

Bài 1: Tính B = 1 + 2 + 3 +…+ 98 + 99

Hướng dẫn giải

Cách giải 1:

B = 1 + 2 + 3 +…+ 98 + 99

= 1 + (2 + 3 + 4 +…+98 + 99

Số số hạng trong ngoặc = (99 – 2) : 1 + 1 = 98 (số hạng), nếu chia thành các cặp, ta có 49 cặp nên tổng đó là:

(2+99) +(3+98) +…+(50+51) = 49.101= 4949

Khi đó B = 1 + 4949 = 4950

Cách giải 2:

B = 1 + 2 + 3 +….+97 + 98 + 99

B = 99 + 98 + 97 +…+ 3 + 2 + 1

2B = 100 + 100 + ….+100

=> 2B = 100.99 => B = 50.99 = 4950

Cách giải 3:

Số số hạng trong dãy = (99 – 1) : 1 +1 = 99 (số hạng)

Trong đó:

99 là số hạng cuối

1 là số hạng đầu

1 là đơn vị khoảng cách giữa các số hạng trong dãy

Tổng các số hạng trong dãy = (99 + 1) . 99 : 2 = 4950

Trong đó:

99 là số hạng cuối

1 là số hạng đầu

99 là số số hạng trong dãy

Ta có công thức tổng quát tính tổng số hạng trong dãy như sau:

Bước 1: Tìm số số hạng trong dãy = (số hạng cuối – số hạng đầu) : đơn vị khoảng cách + 1

Bước 2: Tổng số hạng trong dãy = (Số hạng cuối + số hạng đầu) . Số số hạng trong dãy : 2

Các bài tập tương tự

Bài 2: Tính A = 1 + 3 + 5 +..+ 997 + 999

Đáp án: 250000

Bài 3: Tính C = 2 + 4 + 6 +…+ 96 + 98.

Đáp số: 2450

Bài 4: Tính D = 10 + 12 + … 994 + 996 + 998

Đáp số: 249480

Dạng 2: Tìm tổng của dãy số mà các số hạng không cách đều

Bài 1: Tính A = 1.2 + 2.3 + 3.4 +…+n. (n+1)

Hướng dẫn giải

Cách giải 1:

Ta thấy rằng mỗi số hạng trong dãu số trên đều là tích của hai số tự nhiên liên tiếp, khi đó:

Gọi a1 = 1.2 → 3a1 = 1.2.3 → 3a1 = 1.2.3 – 0.1.2

Tương tự:

a2 = 2.3 → 3a2 = 2.3.3 → 3a2 = 2.3.4 – 1.2.3

a3 = 3.4 → 3a3 = 3.3.4 → 3a3 = 3.4.5 – 2.3.4

…

a(n – 1) = (n – 1).n → 3a(n – 1) = 3(n – 1)n → 3a(n – 1) = (n – 1).n.(n + 1) – (n – 2).(n – 1).n

an = n.(n – 1) → 3an = 3n(n + 1) → 3an = n(n + 1)(n + 2) – (n – 1)n(n + 1)

Cộng vế với vế của các đẳng thức trên ta được:

3(a1 + a2 + a3 +…+ an) = n(n + 1)(n + 2)

$Rightarrow A = frac{n (n+1)(n+2)}{3}$

Cách giải 2:

Ta có:

3A = 1.2.3 + 2.3.3 + … + n(n + 1).3

3A = 1.2.(3 – 0) + 2.3.(3 – 1) + … + n(n + 1)[(n – 2) – (n – 1)]

3A = 1.2.3 – 1.2.0 + 2.3.3 – 1.2.3 + …+ n(n + 1)(n + 2) – (n -1)n(n + 1)

3A = n(n + 1)(n + 2)

$Rightarrow A = frac{n (n+1)(n+2)}{3}$

Từ cách giải trên, rút ra công thức tổng quát cho dạng bài tính tổng của dãy số mà các số hạng không cách đều:

k(k + 1)( k + 2) – (k -1)k(k + 1) = 3k(k + 1). Trong đó k = 1; 2; 3;…

Các bài tập tương tự

Bài 2: Tính B = 1.2.3 + 2.3.4 + … + (n – 1)n(n + 1)

Đáp án: $B = frac{(n-1).n.(n+1)(n+2)}{4}$

Bài 3: Tính C = 1.4 + 2.5 + 3.6 + …+ n(n + 3)

Đáp án: $C = frac{(n+5).n.(n+1)}{3}$

Bài 4: Tính D = 12 + 22 + 32 + … + n2

Đáp án: $D = frac{(2n+1).n.(n+1)}{6}$

Dạng 3: Toán hình

Bài 1: Cho tam giác ABC nhọn. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:

a. Tam giác ABE bằng tam giác ADC

b. Góc BMC bằng 120°

Bài 2: Cho tam giác ABC có ba góc nhọn, đường cao AH. Ở miền ngoài của tam giác ABC vẽ các tam giác vuông cân ABE và tam giác ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).

a. Chứng minh rằng: EM + HC = NH

b. Chứng minh rằng: EN // FM

Bài 3: Cho cạnh hình vuông ABCD có độ dài là 1. Trên các cạnh AB, AD lấy các điểm P,Q sao cho chhu vi của DAPQ = 2. Chứng minh rằng: góc PCQ = 45°

Bài 4: Cho tam giác vuông ABC có cạnh AB = AC, tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D.

a. Chứng minh rằng: BE = CD; AD = AE

b. Gọi I là giao điểm của BE và CD. AI cắt BC tại M, chứng minh rằng MAC là tam giác vuông cân.

c. Từ A và D vẽ các đường thẳng vuông góc với BE, các đường này cắt BC lần lượt ở K và H. Chứng minh rằng KH = KC

Bài 5: Cho đoạn thẳng MN = 4 cm, điểm O nằm giữa hai điểm M và N. Trên cùng một nửa mặt phẳng bờ MN vẽ tam giác cân đỉnh ) là OMA và OMB sao cho góc ở đỉnh O bằng 45°. Tìm vị trí của O để AB min. Tính độ dài nhỏ nhất đó.

Bài 6: Cho tam giác ABC. qua A vẽ đường thăng xy // BC. Tiwf điểm M trên cạnh BC vẽ các đường thẳng song song với AB, Ac chúng cắt xy theo thứ tự tại D và E. Chứng minh rằng:

a. Tam giác ABC = tam giác MDE

b. Ba đường thẳng AM, BD, CE cùng đi qua một điểm.

Bài 7: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt tại M, N. Chứng kinh rằng:

a. DM = EN

b. Đường thẳng BC cắt MN tại trung điểm của I của đoạn MN

c. Đường thẳng vuông góc với MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.

Bài 8: Cho tam giác ABC có góc B và góc C là góc nhọn. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.

a. Chứng minh rằng: BE = CD

b. Gọi M là trung điểm của BE, N là trung điểm của CB. Chứng minh rằng M, A, N thẳng hàng.

c. Ax là tia bất kỳ nằm giữa hai tia AB và AC. Gọi H, K lần lượt là hình chiếu của B, C trên tia Ax. chứng minh rằng BH + CK nhỏ hơn hoặc bằng BC.

Bài 9: Cho tam giác ABC, dựng tam giác đều MAB, NBC, PAC thuộc miền ngoài của tam giác ABC. Chứng minh rằng MC = NA = PB và góc tạo bởi hai đường thẳng ấy bằng 60°, ba đường thẳng MC, NA, PB đồng quy.

Bài 10: Cho tam giác nhọn ABC. Các đường cao AH, BK. CL cắt nhau tại I. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB. Gọi P, Q, R lần lượt là trung điểm của IA, IB, IC. Chứng minh rằng PD, QE, RF đồng quy. Gọi J là điểm đồng quy, chứng minh I là trung điểm của mỗi đường.

Bài 11: Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD tại K. chứng minh AK + CE = BE.