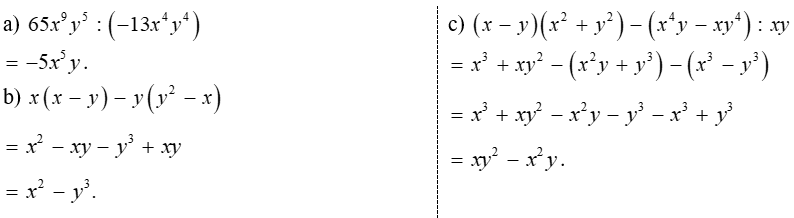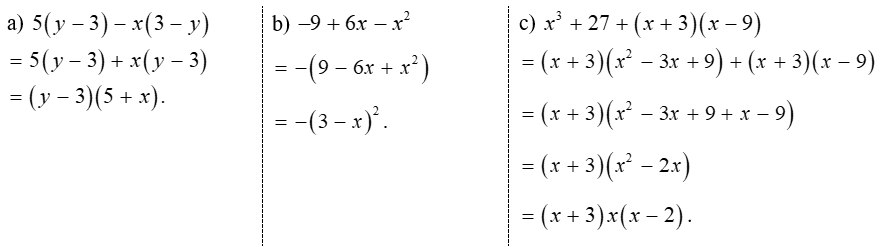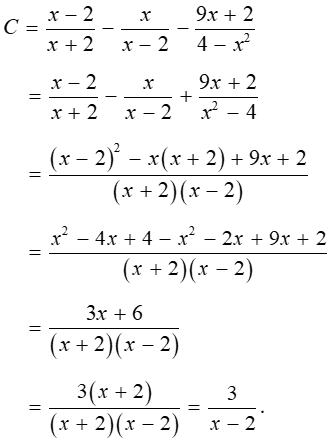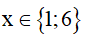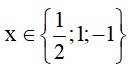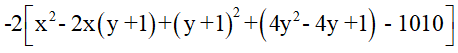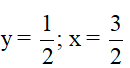Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 8

Bạn đang xem: Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 8 tại truongptdtntthptdienbiendong.edu.vn

1. Đề thi ôn luyện học sinh giỏi môn Toán lớp 8 chuẩn nhất:

Đề bài

Bài 1: (3đ)

a) Phân tích đa thức x³ – 5x² + 8x – 4 thành nhân tử

b) Tìm giá trị nguyên của x để A B biết

A = 10x² – 7x – 5 và B = 2x – 3 .

c)Cho x + y = 1 và x y 0 . Chứng minh rằng

$frac{x}{y^{3}-1}-frac{y}{x^{3}-1}+frac{2(x-y)}{x^{2} y^{2}+3}=0$

Bài 2: (3đ) Giải các phương trình sau:

a) (x²+ x)² + 4(x² + x) = 12

$b) frac{x+1}{2008}+frac{x+2}{2007}+frac{x+3}{2006}=frac{x+4}{2005}+frac{x+5}{2004}+frac{x+6}{2003}$

Bài 3: (2đ) Cho hình vuông ABCD; Trên tia đối tia BA lấy E, trên tia đối tia CB lấy F sao cho AE = CF

a) Chứng minh EDF vuông cân

b) Gọi O là giao điểm của 2 đường chéo AC và BD. Gọi I là trung điểm EF. Chứng minh O, C, I thẳng hàng.

Bài 4: (2) Cho tam giác ABC vuông cân tại A. Các điểm D, E theo thứ tự di chuyển trên AB, AC sao cho BD = AE. Xác định vị trí điểm D, E sao cho:

a/ DE có độ dài nhỏ nhất

b/ Tứ giác BDEC có diện tích nhỏ nhất.

Đáp án

Bài 1: (3 điểm)

a) ( 0,75đ)

x³– 5x²+ 8x – 4 = x³– 4x²+ 4x – x² + 4x – 4 (0,25đ)

= x( x² – 4x + 4) – ( x² – 4x + 4) (0,25đ)

= ( x – 1 ) ( x – 2 ) ² (0,25đ)

b) (0,75 đ)

$Xét frac{A}{B}=frac{10 x^{2}-7 x-5}{2 x-3}=5 x+4+frac{7}{2 x-3}$

$begin{array}{l} text { Với } x in Z text { thì } A: B text { khi } frac{7}{2 x-3} in Z Rightarrow 7 vdots(2 x-3) \ text { Mà } U^{prime}(7)={-1 ; 1 ;-7 ; 7} Rightarrow x=5 ;-2 ; 2 ; 1 text { thì } A vdots B end{array}$

c) $frac{x}{y^{3}-1}-frac{y}{x^{3}-1}=frac{x^{4}-x-y^{4}+y}{left(y^{3}-1right)left(x^{3}-1right)}$

$begin{array}{l} =frac{left(x^{4}-y^{4}right)-(x-y)}{x yleft(y^{2}+y+1right)left(x^{2}+x+1right)}(text { do } x+y=1 Rightarrow y-1=-x text { và } x-1=-y)(0,25 d) \ =frac{(x-y)(x+y)left(x^{2}+y^{2}right)-(x-y)}{x yleft(x^{2} y^{2}+y^{2} x+y^{2}+y x^{2}+x y+y+x^{2}+x+1right)} end{array}$

$begin{aligned} &=frac{(x-y)left(x^{2}+y^{2}-1right)}{x yleft[x^{2} y^{2}+x y(x+y)+x^{2}+y^{2}+x y+2right]}\ &=frac{(x-y)left(x^{2}-x+y^{2}-yright)}{x yleft[x^{2} y^{2}+(x+y)^{2}+2right]}=frac{(x-y)[x(x-1)+y(y-1)]}{x yleft(x^{2} y^{2}+3right)}\ &=frac{(x-y)[x(-y)+y(-x)]}{x yleft(x^{2} y^{2}+3right)}=frac{(x-y)(-2 x y)}{x yleft(x^{2} y^{2}+3right)}\ &=frac{-2(mathrm{x}-mathrm{y})}{mathrm{x}^{2} mathrm{y}^{2}+3} } end{aligned}$

Bài 2: (3 đ)a) (1,25đ)

(x² + x )² + 4(x² + x) = 12 đặt y = x² + x

y² + 4y – 12 = 0 y² + 6y – 2y -12 = 0 (0,25đ)

(y + 6)(y – 2) = 0 y = – 6; y = 2 (0,25đ)

*x² + x = – 6 vô nghiệm vì x² + x + 6 > 0 với mọi x (0,25đ)

* x² + x = 2 x² + x – 2 = 0 x² + 2x – x – 2 = 0 (0,25đ)

x(x + 2) – (x + 2) = 0 (x + 2)(x – 1) = 0 x = – 2; x = 1 (0,25đ)

Vậy nghiệm của phương trình x = – 2 ; x =1

$text { b) }(1,75 mathrm{~d}) quad frac{mathrm{x}+1}{2008}+frac{mathrm{x}+2}{2007}+frac{mathrm{x}+3}{2006}$

$=frac{mathrm{x}+4}{2005}+frac{mathrm{x}+5}{2004}+frac{mathrm{x}+6}{2003} Leftrightarrowleft(frac{mathrm{x}+1}{2008}+1right)+left(frac{mathrm{x}+2}{2007}+1right)+left(frac{mathrm{x}+3}{2006}+1right)\$

$=left(frac{mathrm{x}+4}{2005}+1right)+left(frac{mathrm{x}+5}{2004}+1right)+left(frac{mathrm{x}+6}{2003}+mathrm{l}right)$

$Leftrightarrow frac{x+2009}{2008}+frac{x+2009}{2007}+frac{x+2009}{2006}$

$=frac{x+2009}{2005}+frac{x+2009}{2004}+frac{x+2009}{2003}$

$Leftrightarrow frac{x+2009}{2008}+frac{x+2009}{2007}+frac{x+2009}{2006}-frac{x+2009}{2005}-frac{x+2009}{2004}-frac{x+2009}{2003}=0\$
$Leftrightarrow_{(x+2009)left(frac{1}{2008}+frac{1}{2007}+frac{1}{2006}-frac{1}{2005}-frac{1}{2004}-frac{1}{2003}right)=0}(0,5 mathrm{~d})$

$mathrm{Vì} frac{1}{2008}<frac{1}{2005} ; frac{1}{2007}<frac{1}{2004} ; frac{1}{2006}<frac{1}{2003}\$

Do đó : $frac{1}{2008}+frac{1}{2007}+frac{1}{2006}-frac{1}{2005}-frac{1}{2004}-frac{1}{2003}<0$

,…………

2. Đề thi ôn luyện học sinh giỏi môn Toán lớp 8 mới nhất:

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.

Câu 1. Biểu thức nào sau đây là đơn thức thu gọn?

A. -5xy²;

B. xyz + xz;

C. 2(x² + y²);

D. -3x4yxz.

Câu 2. Các đơn thức nào sau đây đồng dạng với nhau?

A. Đơn thức A và đơn thức C;

B. Đơn thức B và đơn thức C;

C. Đơn thức A và đơn thức B;

D. Cả ba đơn thức A, B, C đồng dạng với nhau.

Câu 3. Giá trị của biểu thức A tại x = 3, y = -4 là

A. -32;

B. -28;

C. 16;

D. 86.

Câu 4. Hằng đẳng thức có tên là

A. bình phương của một tổng;

B. bình phương của một hiệu;

C. tổng hai bình phương;

D. hiệu hai bình phương.

Câu 5. Quy đồng mẫu thức hai phân thức, ta được mẫu thức chung là

A. x²y;

B. xy²;

C. x²y²;

D. x³y³.

Câu 6. Kết quả của phép tính

A. -1;

B. 1;

Câu 7. Hình nào sau đây là hình chóp tam giác đều?

A. Hình có đáy là tam giác;

B. Hình có đáy là tam giác đều;

C. Hình có đáy là tam giác đều và tất cả các cạnh đều vuông góc với mặt đáy;

D. Hình có đáy là tam giác đều và tất cả các cạnh bên bằng nhau.

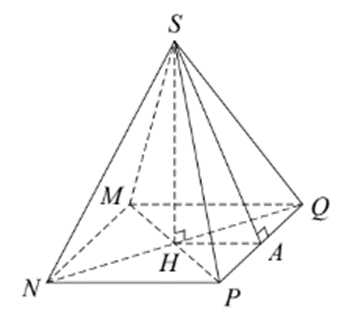
Câu 8. Cho hình vẽ bên, trung đoạn của hình chóp tứ giác S.MNPQ là

A. SH;

B. SA;

C. HA;

D. NQ hoặc MP.

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm) Thu gọn biểu thức:

Bài 2. (1,5 điểm)

Bài 3. (1,5 điểm) Cho biểu thức

a) Tìm điều kiện xác định của biểu thức A.

b) Tìm biểu thức C sao cho C = A – B

c) Tính giá trị của biểu thức C khi 3x(2x + 1) – 6(2x + 1) = 0.

Bài 4. (3,0 điểm)

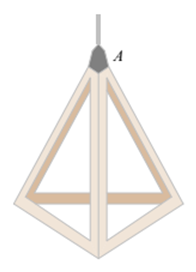
1. Cho tứ giác ABCD. Tính số đo các góc ngoài tại đỉnh D của tứ giác ABCD.

2. Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm.

a) Tính độ dài trung đoạn của hình chóp.

b) Tính diện tích xung quanh của chiếc đèn.

c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là 1 m là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí A) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?

—–HẾT—–

ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 1

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)

Bảng đáp án trắc nghiệm:

Câu	1	2	3	4	5	6	7	8
Đáp án	A	C	A	D	C	B	D	B

PHẦN II. TỰ LUẬN (8,0 điểm)

Bài 1. (1,5 điểm)

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

Bài 2. (1,5 điểm)

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

Bài 3. (1,5 điểm)

a) Điều kiện xác định của biểu thức A là x + 2 ≠ 0 hay x ≠ -2.

b) Với x ≠ ±2, ta có: C = A – B

Suy ra C = $x-2x+2-xx-2+9x+24-x2″> x - 2 x + 2 - (x x - 2 + 9 x + 2 4 - x 2)$

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

c) Ta có:

3x (2x + 1) – 6(2x + 1) = 0

(2x + 1)(3x – 6) = 0

2x + 1 = 0 hoặc 3x – 6 = 0

x = $-12″> - 12 -12$ (thỏa mãn) hoặc x = 2 (không thỏa mãn).

Thay x = $-12″> - 12 -12$ vào biểu thức C = $3x-2″> 3 x - 2 3-2$ ta được:

C = $3-12-2=3-52=-65″> 3 - 12 - 2 = 3 - 52 = - 6 5 3-12-2=3-52=-65$ .

Bài 4. (3,0 điểm)

1.Xét tứ giác ABCD, ta có $A^+B^+C^+D^=360°”> ˆ A + ˆ B + ˆ C + ˆ D =360°$

Do đó $75°+90°+120°+D^=360°”> 75 ° + 90 ° + 120 ° + ˆ D = 360 ° 75°+90°+120°=360°$

Hay $285°+D^=360°”> 285 ° + ˆ D = 360 ° 285°=360°$

Suy ra $D^=360°-285°=75°”> ˆ D = 360 ° - 285 ° = 75 ° =360°-285°=75°$

Khi đó góc ngoài tại đỉnh D của tứ giác là $180°-75°=105°.”> 180 ° - 75 ° = 105 ° . 180°-75°=105°.$

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

b) Chu vi đáy của hình chóp là: C = 3BD = 3.20 = 60cm.

Diện tích xung quanh của chiếc đèn là:

$Sxq=12C.AH=12.60.103=3003″> S x q = 12 C . A H =12.60.103=3003$ cm2.

c) Vì ∆ADCvà ∆BDCđều là các tam giác đều có cạnh 20 cm nên hai đường cao AHvà BHcủa hai tam giác bằng nhau.

Vì Olà trọng tâm ∆BDC nên $OH=13BH=1033″> O H =1033$ cm.

∆AOH vuông tại O, theo định lí Pythagore ta có:

AO2 = AH2 – OH2 = $300-10332=300-3009=8003″> 300 - (10 \sqrt 3 3) 2 = 300 - 3009 = 8003 300-10332=300-3009=8003$

Suy ra AO = $8003\approx16,3″> \sqrt 8003 \approx 16, 3 8003\approx16,3$ cm.

Khi đó bạn Nam cần đưa dây diện từ đầu đèn tới trần nhà khoảng là 100 – 16,3 = 83,7cm.

Bài 5. (0,5 điểm)

Đề thi Giữa kì 1 Toán 8 Cánh diều có đáp án (10 đề + ma trận)

3. Đề thi ôn luyện học sinh giỏi môn Toán lớp 8 chi tiết nhất:

I. PHẦN TRẮC NGHIỆM (2 ĐIỂM)

Hãy viết vào tờ giấy thi chữ cái in hoa đứng trước câu trả lời đúng

Câu 1. Khai tiển biểu thức x³-8x³ ta được kết quả là:

A. (x-2y)³ B. x³-2y³

C. (x-2y)(x²+2xy+4y²) D. x³-6x²y + 12xy²-8y³

Câu 2. Kết quả phép tính -x²(3-2x)là:

A. 3x²-2x³ B.2x³-3x² C.-3x³+2x² D.-4x²

Câu 3. Để 4y²-12y + Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

trở thành một hằng đảng thức. Giá trị trong ô vuông là:

A. 6 B. 9 C. – 9 D. Một kết quả khác

Câu 4. Biểu thức 101² – 1 có giá trị bằng

A. 100 B. 100² C. 102000 D. Một kết quả khác

Câu 5. Giá trị của biểu thức x²+2xy+y² tại x = – 1 và y = – 3 bằng

A. 16 B. – 4 C. 8 D. Một kết quả khác

Câu 6. Biết 4x(x²-25)=0, các số x tìm được là:

A. 0; 4; 5 B. 0; 4 C. -5; 0; 5 D. Một kết quả khác

Câu 7.

A. -2x +4 =2(2-x) B. -2x+4 = -2(2-x)

C. -2x +4= -2(x+2) D. -2x+4= 2(x-2)

Câu 8. Thực hiện phép nhân x(x-y)

A.x²-y B.x-xy C.x-x² D.x²-xy

II. PHẦN TỰ LUẬN (8 ĐIỂM)

Bài 1 (1,5đ): Phân tích các đa thức sau thành nhân tử

a. 36a⁴-y² b. 6x² +x -2

Bài 2 (1,5đ). Tìm x, biết:

a. x( x-4)+1 = 3x-5 b. 2x³-3x²-2x+3= 0

Bài 3 (1,5đ).

a. Cho biểu thức A= x³-9x²+27x -27 . Tính giá trị của A khi x = 1.

b. Tìm đa thức thương và đa thức dư trong phép chia đa thức A (x) cho B (x). Biết:

A(x)= 2x³+x²-x+ a và B(x) = x-2

Bài 4 (3,0đ). Cho hình bình hành ABCD có AB > BC. Đường phân giác của góc cắt AB tại M, đường phân giác của góc cắt CD tại N.

a. Chứng minh AM = CN.

b. Chứng minh tứ giác DMBN là hình bình hành.

c. Gọi H, K lần lượt là hình chiếu của N và N trên BN và DM. Chứng minh hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường.

Bài 5 (0,5đ). Tìm giá trị lớn nhất của biểu thức:

A = -2x² -10y² +4xy +4x+ 4y +2016

HƯỚNG DẪN CHẤM

I. PHẦN TRẮC NGHIỆM (2 ĐIỂM)

Câu 1: C (0,25đ)

Câu 2: B (0,25đ)

Câu 3: B (0,25đ)

Câu 4: C (0,25đ)

Câu 5: A (0,25đ)

Câu 6: C (0,25đ)

Câu 7: A (0,25đ)

Câu 8: D (0,25đ)

II. PHẦN TỰ LUẬN (8 ĐIỂM)

Bài 1

a. 36a⁴-y2= (6a)²-y²= (6a-y)(6a+y) (0,75đ)

b.6x² +x -2 = 6x²+4x -3x -2

= 2x( 3x+2) – (3x+2) = (2x-1)(3x+2) (0,75đ)

Bài 2

a. x(x-4) +1 = 3x-5

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

x(x-1) – 6(x-1)=0 (0,25đ)

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

(x-1)(x-6)=0 (0,25đ)

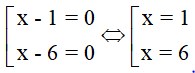
Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

Vậy Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

là giá trị cần tìm. (0,25đ)

b. 2x³-3x²-2x+3= 0

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

x²( 2x-3) -(2x-3) =0 (0,25đ)

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

(2x-3)(x²-1) =0

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

(2x-3)(x-1)(x+1)=0 (0,25đ)

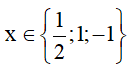
Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

…..

Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

Vậy Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

là giá trị cần tìm. (0,25đ)

Bài 3

a. Xét biểu thức:

A= x³-9x²+27x -27

= x³ -3.x².3 +3.x.3²– 3³

=(x-3)³ (0,25đ)

Với x = 1 biểu thức A được viết lại như sau:

A=(1-3)³= -8

Vậy A = – 8 khi x = 1 (0,25đ)

b.Thực hiện đúng được phép chia A(x)= 2x³+x²-x+ a cho B(x) = x-2, tìm được thương bằng:2x²+5x +9 và dư bằng a + 18. (1,0đ)

Bài 4

Vẽ đúng hình (0,25đ)

a. Chứng minh được AM = CN (1,25đ)

b. Chứng minh được tứ giác DMBN là hình bình hành (1đ)

c. Lập luận chặt chẽ chỉ ra được hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường (0,5đ)

Bài 5

A = -2x² -10y² +4xy +4x+ 4y +2016

= Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

(0,25đ)

= -2( x-y-1)² -2(2y-1)² +2020

GTLN của A bằng 2020 khi Đề thi Giữa kì 1 Toán lớp 8 có đáp án năm 2023 Đề 1

(0,25đ)

4. Mẹo đạt điểm cao khi làm Đề thi ôn luyện học sinh giỏi môn Toán lớp 8:

Hiểu rõ kiến thức cơ bản: Đảm bảo bạn đã hiểu rõ kiến thức cơ bản của từng chương trình học trong sách giáo trình. Nắm vững cơ bản giúp bạn dễ dàng tiếp cận các bài toán khó hơn.

Giải nhiều bài tập thực hành: Học Toán đòi hỏi việc thực hành nhiều. Giải nhiều bài tập từ dễ đến khó, từ các nguồn khác nhau để có sự đa dạng trong kiến thức.

Làm các đề thi mẫu: Tìm các đề thi mẫu từ các năm trước để làm. Điều này giúp bạn làm quen với định dạng và cấu trúc của đề thi.

Giữ kỹ thuật giải bài toán: Học cách giải bài toán một cách hệ thống và có kỹ thuật. Sử dụng các phương pháp như phân tích, suy luận, rút gọn biểu thức, hay sử dụng biểu đồ nếu cần thiết.

Lập kế hoạch ôn tập: Lên kế hoạch ôn tập hợp lý để không bị quá tải. Phân chia thời gian để ôn từng phần kiến thức một cách chặt chẽ.

Tìm hiểu cấu trúc đề thi: Nắm vững cấu trúc của đề thi, biết được phần nào làm trước, phần nào làm sau. Điều này giúp bạn quản lý thời gian hiệu quả.

Chú ý đến các dạng bài đặc biệt: Các đề thi thường có một số dạng bài toán đặc biệt. Làm quen với chúng và biết cách giải sẽ giúp bạn tự tin hơn khi làm bài.

Tham gia nhóm ôn tập: Nếu có thể, tham gia các nhóm ôn tập hoặc tìm kiếm sự giúp đỡ từ bạn bè hoặc giáo viên.

Tự kiểm tra và sửa lỗi: Sau khi làm bài, tự kiểm tra lại kết quả và tìm lỗi. Học từ những sai sót của mình để không mắc phải những lỗi tương tự trong tương lai.

Thực hành làm bài tốc độ: Ôn tập cả kỹ năng làm bài nhanh, đặc biệt là trong các kỳ thi có thời gian giới hạn.