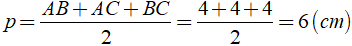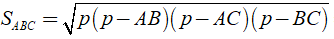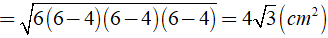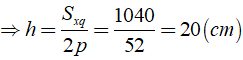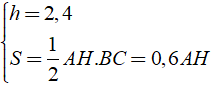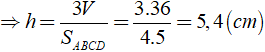Các dạng bài tập hình lăng trụ đứng và hình chóp đều

Bạn đang xem: Các dạng bài tập hình lăng trụ đứng và hình chóp đều tại truongptdtntthptdienbiendong.edu.vn

Hình lăng trụ đứng và hình chóp đều là hai loại hình học không gian hay gặp ở các bài toán tính diện tích và thể tích. Bài viết sẽ cung cấp đầy đủ cônh thức và lý thuyết cần nhớ để học sinh vận dụng làm bài tập một cách nhanh chóng

1. Các dạng bài tập hình lăng trụ đứng:

1.1. Khái niệm hình lăng trụ đứng:

+ Theo như định nghĩa, hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên 2 mặt phẳng song song nhau và là 2 đa giác bằng nhau. Theo đó 2 đáy này có thể là hình vuông, hình bình hành, hình tam giác hoặc hình chữ nhật,… Đồng thời những mặt bên là hình bình hành và có các cạnh bên bằng nhau và song song với nhau.

+ Theo như định nghĩa về hình lăng trụ, hình lăng trụ đứng chính là hình có:

Hai đáy của hình lăng trụ này là hai đa giác phẳng và bằng nhau, nằm trên 2 mặt phẳng song song nhau.

Những mặt bên của hình lăng trụ này vuông góc với những mặt phẳng có chứa những đa giác đáy. Đối với hình lăng trụ này, các mặt bên sẽ là những hình chữ nhật.

Đối với hình lăng trụ dạng đứng, độ dài của cạnh bên chính là chiều cao của hình lăng trụ này, những cạnh bên song song và bằng với nhau. Thông thường người ta sẽ gọi tên những hình lăng trụ đứng theo như tên của đa giác đáy như lăng trụ tứ giác, lăng trụ tam giác,… Hình lăng trụ dạng đứng có đáy là những đa giác đều sẽ gọi là lăng trụ đều.

1.2. Tính chất của hình lăng trụ đứng:

Đây là loại hình lăng trụ có những cạnh bên nằm vuông góc với đáy.

Tất cả những mặt bên của hình lăng trụ này sẽ là hình chữ nhật.

Hình lăng trụ này có những mặt phẳng chứa đáy là những mặt phẳng song song nhau.

Cạnh bên chính là chiều cao của hình này.

1.3. Công thức tính thể tích và diện tích xung quanh:

+ Công thức tính diện tích xung quanh của hình lăng trụ đứng bằng chiều cao của hình lăng trụ nhân với chu vi đáy.

Sxq = 2.p.h (Trong đó: p là nửa chu vi đáy và h là chiều cao của hình)

+ Công thức tính diện tích hình lăng trụ đứng toàn phần bằng tổng của diện tích hai đáy và diện tích xung quanh.

Stp = Sxq + 2Sđáy

+ Công thức tính thể tích hình lăng trụ đứng bằng tính của diện tích đáy nhân với chiều cao.

V = S . h (Trong đó S là diện tích đáy của hình và h là chiều cao)

1.4. Các dạng bài tập về hình lăng trụ đứng:

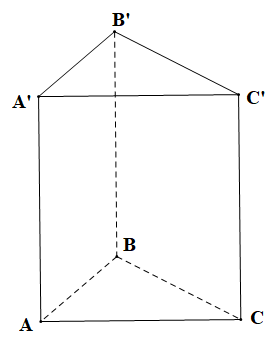
Bài 1: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, AB = 4cm,AA’ = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ ABC.A’B’C’ ?

Lý thuyết Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Lời giải:

Xét tam giác ABC có nửa chu vi của tam giác là:

Lý thuyết Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Khi đó ta có

Lý thuyết Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

+ Diện tích xung quanh của hình lăng trụ Sxq = 2p.AA’ = 2.6.5 = 60( cm2 )

+ Diện tích toàn phần của hình lăng trụ là Stp = Sxq + 2SABC = 60 + 2.4√ 3 = 60 + 8√ 3 ( cm2 )

+ Thể tích của hình lăng trụ là V = S.AA’ = 4√ 3 .5 = 20√ 3 ( cm^3 ).

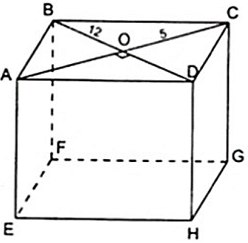
Bài 2: Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm2

Lời giải:

Bài tập Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Áp dụng công thức: Stp = Sxq + 2Sd

Hay Sxq = Stp – 2Sd = 1280 – 2.1/2.1024

= 1280 – 240 = 1040( cm2 )

Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)

Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:

BC2 = BO2 + OC2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )

Chu vi đáy là 2p = 4.13 = 52( cm )

Áp dụng công thức Sxq = 2p.h

Bài tập Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Bài 3: Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm3 ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?

Lời giải:

Bài tập Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h

Ta có: Bài tập Hình lăng trụ đứng | Lý thuyết và Bài tập Toán 8 có đáp án

Do đó: V = S.h = 0,6AH.2,4 = 1,44AH

Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

Bài 4: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Hãy tính thể tích hình lăng trụ này?

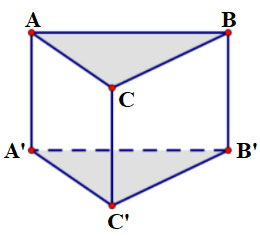
Hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều

Giải:

Vì đáy là tam giác đều cạnh a nên diện tích: $S_{A B C}=a^2 cdot frac{sqrt{3}}{4}=2^2 cdot frac{sqrt{3}}{4}=sqrt{3}left(m^2right)$

Khi này, thể tích hình lăng trụ là:

$V=S_{A B C} cdot h=sqrt{3} cdot 3=3 sqrt{3}left(m^3right)$

Bài 5: Cho hình hộp đứng có các cạnh AB = 3a, AD = 2a, AA’= 2a. Tính thể tích của khối A’.ACD’

Hướng dẫn:

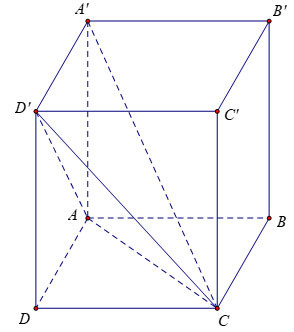
Cho hình hộp đứng

Do mặt bên ADD’A’ là hình chữ nhật nên ta có:

$S_{A A^{prime} D^{prime}}=frac{1}{2} S_{A A^{prime} D^{prime} D}$

$V_{A^{prime} cdot A C D^{prime}}=V_{C cdot A A^{prime} D^{prime}}=frac{1}{2} V_{C cdot A A^{prime} D^{prime} D}$

$=frac{1}{2} cdot frac{1}{3} V_{A B C D cdot A^{prime} B^{prime} C^{prime} D^{prime}}$

$=frac{1}{6} cdot 3 a cdot 2 a cdot 2 a=2 a^3$

2. Hình chóp đều:

2.1. Khái niệm hình chóp đều:

Hình chóp đều là hình chóp có mặt đáy là một đa giác đều (tam giác đều, hình vuông,…), có mặt bên là các tam giác cân bằng nhau và có chung đỉnh.

2.2. Tính chất của hình chóp đều:

+ Về cơ bản, tính chất của loại hình này bao gồm những yếu tố sau:

Hình chóp tam giác đều có tính chất là hình có 3 mặt phẳng nằm đối xứng với nhau.

Các cạnh bên của hình chóp tam giác đều bằng nhau và có đáy là hình tam giác đều.

Chân đường cao của hình chóp trùng với trọng tâm của mặt đáy.

Mọi góc của hình chóp được tạo nên bởi mặt bên cũng như mặt đáy đều bằng nhau.

Các góc được tạo nên bởi mặt đáy cũng như cạnh bên đều bằng nhau.

+ Một trong những tính chất quan trọng khác trong chương trình đó chính là kiến thức liên quan đến hình chóp tứ giác đều. Tính chất hình chóp tứ giác đều bao gồm những yếu tố sau:

Đáy của hình chóp tứ giác đều là hình vuông.

Các cạnh bên đều bằng nhau.

Các mặt bên của hình chóp tứ giác đều là những tam giác cân bằng nhau.

Chân đường cao của hình chóp trùng với giao điểm 2 đường chéo của mặt đáy.

Tất cả những góc được tạo ra từ cạnh bên cũng như mặt đáy đều bằng nhau.

2.3. Các tính diện tích xung quanh và thể tích hình chóp đều:

– Diện tích xung quanh hình chóp đều

Dựa vào tính chất hình chóp đều ta có công thức tính diện tích xung quanh của hình chóp đều là tích của trung đoạn của hình chóp đều nhân với nửa chu vi đáy.

Công thức tổng quát tính diện tích xung quanh của hình chóp đều:

Sxq=p×d

Trong đó:

d là trung đoạn

p là nửa chu vi đáy.

Sxq: Diện tích xung quanh

– Diện tích toàn phần hình chóp đều

Dựa vào tính chất hình chóp đều ta có công thức tính diện tích toàn phần của hình chóp đều là tổng của diện tích xung quanh và diện tích đáy.

Công thức tổng quát tính diện tích toàn phần của hình chóp đều:

Stp=Sxq+Sđáy

Trong đó:

Sđáy là diện tích mặt đáy

Sxq: Diện tích xung quanh

Stp: Diện tích toàn phần

Đối với diện tích đáy cần tùy thuộc vào dạng đáy mà áp dụng những công thức tính khác nhau.

– Thể tích hình chóp đều

Công thức tổng quát tính thể tích hình chóp đều cụ thể là:

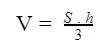
Trong đó:

S là diện tích đáy và tùy thuộc vào mỗi hình đáy mà có những công thức tính diện tích đáy khác nhau.

h là chiều cao.

V là thể tích.

3. Bài tập vận dụng và lời giải:

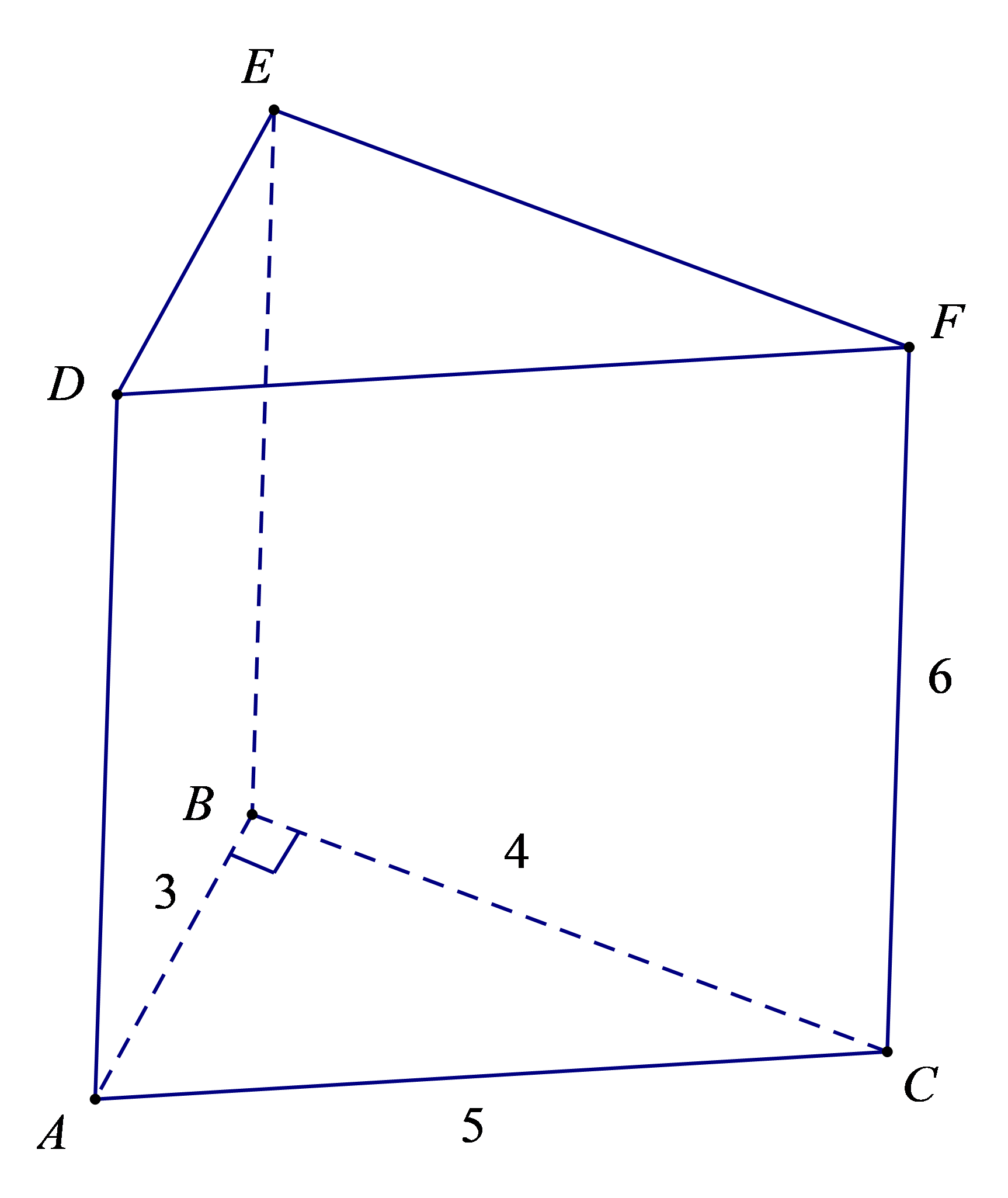
Bài 1. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác biết, đáy của nó là tam giác vuông và các kích thước như hình vẽ (đơn vị của các cạnh là cm).

Hướng dẫn giải

Ta tính chu vi đáy là tam giác ABC: C = 3 + 4 + 5 = 12 (cm), chiều cao h = 6 cm.

Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:

Sxq = C . h = 12 . 6 = 72 (cm2).

Ta tính diện tích đáy $S=12\cdot3\cdot4=6″> S = 6$ (cm2).

Thể tích của hình lăng trụ đứng tam giác ABC.DEF là:

V = S.h = 6 . 6 = 36 (cm3).

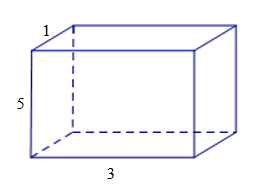
Bài 2. Tính diện tích xung quanh và thể tích của lăng trụ đứng tứ giác, biết đáy của nó là hình chữ nhật (độ dài các cạnh đơn vị cm).

Hướng dẫn giải

Ta tính chu vi đáy C = 2(1 + 3 ) = 8 (cm), chiều cao h = 5 cm

Diện tích của hình lăng trụ đứng tứ giác này là: Sxq = C . h = 8 . 5 = 40 (cm2).

Ta tính diện tích đáy S = 1 . 3 = 3 (cm2)

Thể tích hình lăng trụ đứng tứ giác là: V = S . h = 3 . 5 = 15 (cm3).

Bài 3. Số cạnh của hình lăng trụ đứng tam giác là?

A. 9 cạnh;

B. 8 cạnh;

C. 5 cạnh;

D. 6 cạnh.

Hướng dẫn giải

Đáp án đúng là: A

Lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.

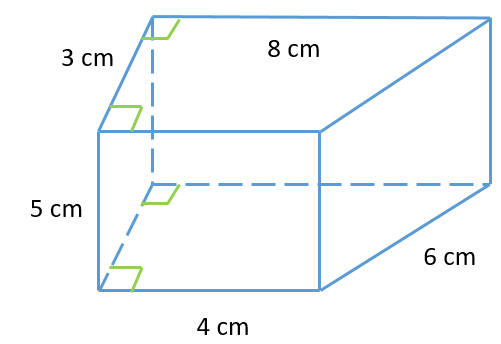
Bài 4. Thể tích hình lăng trụ đứng tứ giác có các kích thước như hình vẽ dưới đây là?

A. V = 80 cm3;

B. V = 18 cm3;

C. V = 19 cm3;

D. V = 90 cm3.

Hướng dẫn giải

Đáp án đúng là: D

Hai mặt đáy của hình lăng trụ đứng tứ giác là hai hình thang bằng nhau nên, diện tích một mặt đáy là: $S=12.(4+8).3=18″> S = 12.(4+8).3=18$ (cm2)

Thể tích hình lăng trụ đứng tứ giác là: V = 18 . 5 = 90 (cm3)

Vậy thể tích hình lăng trụ đứng tam giác là V = 90 cm3.

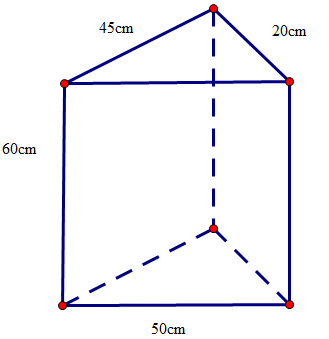
Bài 5. Cho hình lăng trụ đứng tam giác với hai đáy là hai tam giác và các kích thước như hình vẽ.

Diện tích xung quanh của hình lăng trụ đứng tam giác đó bằng?

A. 7 200 cm2;

B. 6 900 cm2;

C. 6 250 cm2;

D. 7 900 cm2.

Hướng dẫn giải

Đáp án đúng là: B

Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:

Sxq = (45 + 20 + 50) . 60 = 6 900 (cm2)

Vậy diện tích xung quanh của hình lăng trụ đứng tam giác là Sxq = 6 900 cm2.

Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là?

A. 6( cm3 ) B. 18( cm3 )

C. 12( cm3 ) D. 9( cm3 )

Lời giải:

Áp dụng công thức thể tích của hình chóp ta có:

V = 1/3h.SABCD = 1/3.2.32 = 6( cm3 )

Chọn đáp án A.

Bài 7: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36( cm3 ). Tính độ dài đường cao của hình chóp?

A. 6( cm ) B. 8( cm )

C. 5,4( cm ) D. 7,2( cm )

Lời giải:

Áp dụng công thức thể tích của hình chóp ta có:

V = 1/3.h.SABCD

Bài tập Các công thức về hình chóp đều | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án C.

Bài 8: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?

A. 32( cm2 ) B. 32√ 2 ( cm2 )

C. 16√ 2 ( cm2 ) D. 16( cm2 )

Lời giải:

Chu vi của đáy ABCD là 2( 4 + 4 ) = 16( cm )

Gọi d là độ dài trung đoạn của hình chóp

Ta có: d = √ (62 – 22) = 4√ 2 ( cm )

Áp dụng công thức diên tích xung quanh của hình chóp: Sxq = p.d

⇒ Sxq = 8.4√ 2 = 32√ 2 ( cm2 )

Chọn đáp án B.