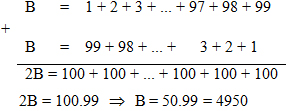Bạn đang xem bài viếtCác dạng toán nâng cao lớp 7 Đề toán lớp 7 tại website Truongptdtntthptdienbiendong.edu.vn có thể kéo xuống dưới để đọc từng phần hoặc nhấn nhanh vào phần mục lục để truy cập thông tin bạn cần nhanh chóng nhất nhé.
CÁC DẠNG TOÁN NÂNG CAO LỚP 7
DẠNG 1: DÃY SỐ MÀ CÁC SỐ HẠNG CÁCH ĐỀU.
Bài 1: Tính B = 1 + 2 + 3 + … + 98 + 99
Lời giải:
Cách 1:
B = 1 + (2 + 3 + 4 + … + 98 + 99).
Ta thấy tổng trong ngoặc gồm 98 số hạng, nếu chia thành các cặp ta có 49 cặp nên tổng đó là:
(2 + 99) + (3 + 98) + … + (51 + 50) = 49.101 = 4949
Khi đó B = 1 + 4949 = 4950
Lời bình: Tổng B gồm 99 số hạng, nếu ta chia các số hạng đó thành cặp (mỗi cặp có 2 số hạng thì được 49 cặp và dư 1 số hạng, cặp thứ 49 thì gồm 2 số hạng nào? Số hạng dư là bao nhiêu?), đến đây học sinh sẽ bị vướng mắc.
Ta có thể tính tổng B theo cách khác như sau:
Cách 2:

Bài 2: Tính C = 1 + 3 + 5 + … + 997 + 999
Lời giải:
Cách 1:
Từ 1 đến 1000 có 500 số chẵn và 500 số lẻ nên tổng trên có 500 số lẻ. Áp dụng các bài trên ta có C = (1 + 999) + (3 + 997) + … + (499 + 501) = 1000.250 = 250.000 (Tổng trên có 250 cặp số)
Cách 2: Ta thấy:

Quan sát vế phải, thừa số thứ 2 theo thứ tự từ trên xuống dưới ta có thể xác định được số các số hạng của dãy số C là 500 số hạng.
Áp dụng cách 2 của bài trên ta có:

Bài 3. Tính D = 10 + 12 + 14 + … + 994 + 996 + 998
Nhận xét: Các số hạng của tổng D đều là các số chẵn, áp dụng cách làm của bài tập 3 để tìm số các số hạng của tổng D như sau:
Ta thấy:

Tương tự bài trên: từ 4 đến 498 có 495 số nên ta có số các số hạng của D là 495, mặt khác ta lại thấy: ![]() hay
hay
số các số hạng = (số hạng đầu – số hạng cuối) : khoảng cách rồi cộng thêm 1
Khi đó ta có:

Thực chất ![]()
Qua các ví dụ trên, ta rút ra một cách tổng quát như sau: Cho dãy số cách đều u1, u2, u3, … un (*), khoảng cách giữa hai số hạng liên tiếp của dãy là d,
Khi đó số các số hạng của dãy (*) là: ![]()
Tổng các số hạng của dãy (*) là: ![]()
Đặc biệt từ công thức (1) ta có thể tính được số hạng thứ n của dãy (*) là: un = u1 + (n – 1)d
Hoặc khi u1 = d = 1 thì ![]()
DẠNG 2: DÃY SỐ MÀ CÁC SỐ HẠNG KHÔNG CÁCH ĐỀU.
Bài 1. Tính A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)
Lời giải:
Cách 1:
Ta thấy mỗi số hạng của tổng trên là tích của hai số tự nhên liên tiếp, khi đó:
Gọi a1 = 1.2 → 3a1 = 1.2.3 → 3a1 = 1.2.3 – 0.1.2
a2 = 2.3 → 3a2 = 2.3.3 → 3a2 = 2.3.4 – 1.2.3
a3 = 3.4 → 3a3 = 3.3.4 → 3a3 = 3.4.5 – 2.3.4
…………………..
an-1 = (n – 1)n → 3an-1 =3(n – 1)n → 3an-1 = (n – 1)n(n + 1) – (n – 2)(n – 1)n
an = n(n + 1) → 3an = 3n(n + 1) → 3an = n(n + 1)(n + 2) – (n – 1)n(n + 1)
Cộng từng vế của các đẳng thức trên ta có:
3(a1 + a2 + … + an) = n(n + 1)(n + 2)![]()
Cách 2: Ta có
3A = 1.2.3 + 2.3.3 + … + n(n + 1).3 = 1.2.(3 – 0) + 2.3.(3 – 1) + … + n(n + 1)[(n – 2) – (n – 1)] = 1.2.3 – 1.2.0 + 2.3.3 – 1.2.3 + … + n(n + 1)(n + 2) – (n – 1)n(n + 1) = n(n + 1)(n + 2)
![]()
* Tổng quát hoá ta có:
k(k + 1)(k + 2) – (k – 1)k(k + 1) = 3k(k + 1). Trong đó k = 1; 2; 3; …
Ta dễ dàng chứng minh công thức trên như sau:
k(k + 1)(k + 2) – (k – 1)k(k + 1) = k(k + 1)[(k + 2) – (k – 1)] = 3k(k + 1)
Download tài liệu để xem chi tiết.
Cảm ơn bạn đã theo dõi bài viết Các dạng toán nâng cao lớp 7 Đề toán lớp 7 tại website Truongptdtntthptdienbiendong.edu.vn nếu thấy bài viết này hữu ích đừng quên để lại bình luận và đánh giá giới thiệu website với mọi người nhé. Xin Chân thành cảm ơn.