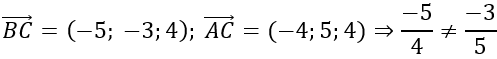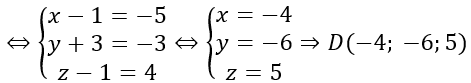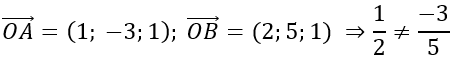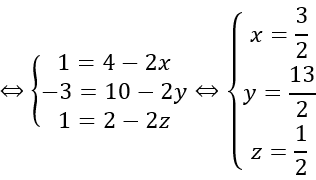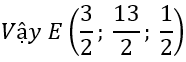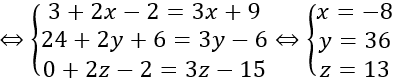1. Kiến thức hình Oxyz:
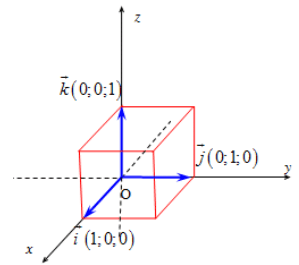
Trong hệ trục không gian, xét ba trục tọa độ Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi tia i, tia j, tia k là các vectơ đơn vị, tương ứng trên Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ trục tọa độ vuông góc trong không gian.
Chú ý: 
2. Công thức hình Oxyz trong hình học không gian:
– Cho A (xA; yA; zA), B(xB; yB; zB)
tia AB = (xB – xA; yB – yA; zB – zA)
Toa độ trung điểm của đoạn thẳng AB: M (xA + xB/2; yA + yB/2; zA + zB/2)
Tọa độ trọng tâm G của tam giác ABC: G (xA + xB + xC/3; yA + yB + yC/3; zA + zB + zC/3)
Tọa độ trọng tâm G của tứ diện ABCD: G (xA + xB + xC + xD/4; yA + yB + yC + yD/4; zA + zB + zC + zD/4 )
– Tích có hướng có hai vectơ
a. Định nghĩa: Trong không gian Oxyz cho hai vectơ a = (a1; a2; a3), vectơ = (b1; b2; b3). Tích có hướng của hai vectơ a và b kí hiệu là [ ] được xác định bởi:
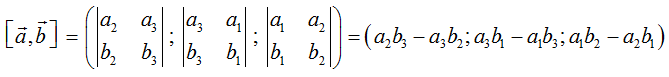
Chú ý: Tích có hướng của hai vecto là một vecto, tích vô hướng của hai vecto là một số.
b. Tính chất:
[] vuông góc
; [
] vuông góc
[ ] = – [
]
[] =
; [
] =
; [
] =
=
.
. sin (
) (chương trình nâng cao)
cùng phương ⇔ [
] =
( chứng minh 3 điểm thẳng hàng)
Chú ý:
– Tích vô hướng của hai vecto thường sử dụng để chứng minh hai đường thẳng vuông góc, tính góc giữa hai đường thẳng.
– Tích có hướng của hai vecto thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể hiện hình hộp; chứng minh các vescto đồng phẳng – không đồng phẳng, chứng minh các vecto cùng phương.
Phương trình mặt cầu:
a. định nghĩa:
Cho điểm I cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách I một khoảng R được gọi là mặt cầu tâm I, bán kính R.
Kí hiệu: S (I; R) ⇔ S (I; R) = { }
b. Vị trí tương đối giữa mặt cầu và mặt phẳng:
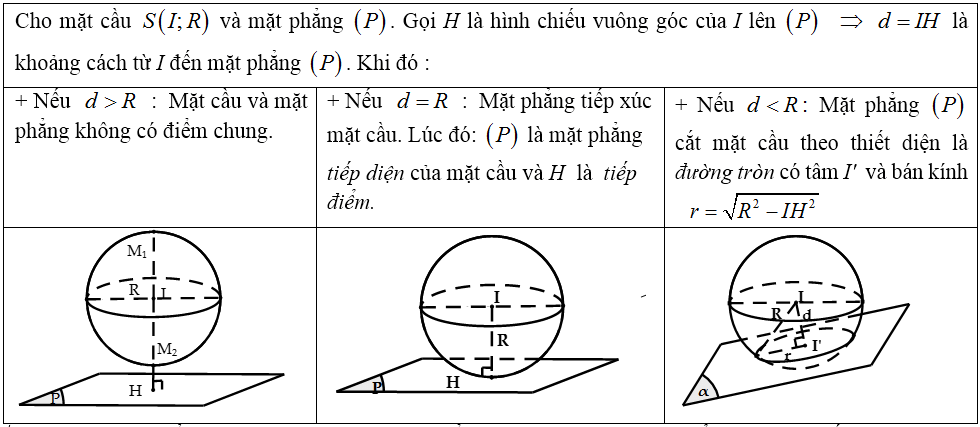Lưu ý: khi mặt phẳng (P) đi qua tâm I thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn.
c. Vị trí tương đối giữa mặt cầu và đường thẳng:
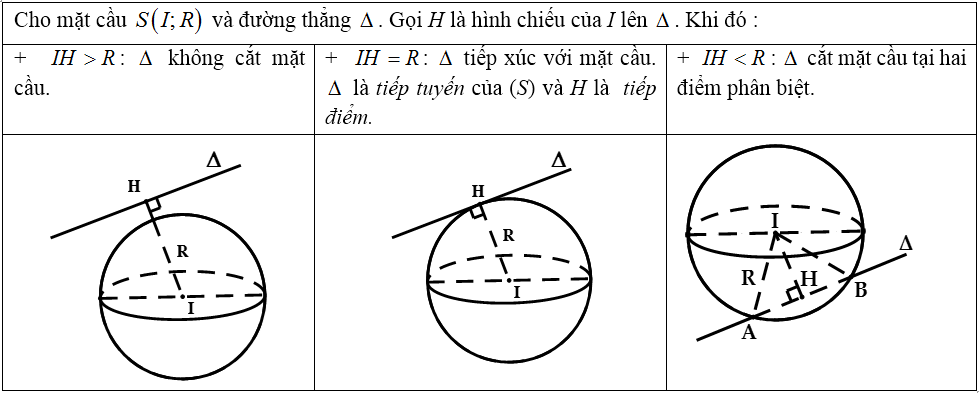
3. Bài tập vận dụng về hình Oxyz:
Câu 1: Cho 2 điểm A(1; 3; 5), B(1; -1; 1) khi đó trung điểm I của AB có tọa độ là:
D. I(1; 1; 3)
Đáp án: D
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;2), B(-2;1;3), C(3;2;4),D(6;9-5) . Hãy tìm tọa độ trọng tâm của tứ diện ABCD?
C. (2;3;1)
D. (-2;3;1)
Đáp án:
Câu 3: Cho điểm A(2; 0; 0), B(0; 2; 0), C(0; 0; 2), D(2; 2; 2). Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là
Đáp án: B
Câu 4: Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13)
D. 2x+y-z-2=0
Đáp án: B
Câu 5: Trong không gian tọa độ Oxyz, cho mặt cầu (S) có đường kính AB, với A (6;2;-5), B (-4;0;7). Viết phương trình mp (P) tiếp xúc với mặt cầu (S) tại A.
A. (P): 5x + y – 6z +62 = 0
B. (P): 5x + y – 6z – 62 = 0
C. (P): 5x – y – 6z – 62 = 0
D. (P): 5x + y + 6z +62 = 0
Đáp án: B
Câu 6: Trong không gian với hệ trục tọa độ Oxyz, có tất cả bao nhiêu số tự nhiên của tham số m để phương phương trình x^2 + y^2 + z^2 + 2(m-2)y -2(m+3)z + 3m^2 +7 =0 là phương trình của một mặt cầu.
Câu 7:Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1; -3;1);B(2;5;1) và vecto OC→=-3 i→+2 j→+5 k→
a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.
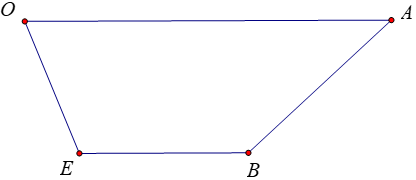
b) Tìm tọa độ điểm E sao cho tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.
c) Tìm tọa độ điểm M sao cho 3 AB→+2 AM→=3 CM→
Lời giải:
a)
⇒BC→; AC→ không cùng phương hay A, B, C không thẳng hàng
Gọi D (x; y; z) ⇒AD→=(x-1;y+3;z-1)
ABCD là hình bình hành ⇔AD→=BC→
b)
Ta có:
⇒OA→; OB→ không cùng phương hay O, A, B không thẳng hàng.
Gọi E (x; y; z) ⇒EB→=(2-x;5-y;1-z)
Theo đề bài, tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.
⇒OA→=2EB→
c) Gọi M (x; y; z). Ta có:
AB→=(1;8;0)⇒3AB→=(3;24;0)
AM→=(x-1;y+3;z-1)⇒2AM→=(2x-2;2y+6;2z-2)
CM→=(x+3;y-2;z-5)⇒3CM→=(3x+9;3y-6;3z-15)
3AB→+2AM→=3CM→
Vậy M(-8; 36; 13)
Câu 8. Viết phương trình mặt cầu (S), trong các trường hợp sau:
a. (S) có tâm I (2; 2; -3) và bán kính R = 3
b. (S) có tâm I (1; 2; 0) và (S) qua P (2; -2; 1)
c. (S) có đường kính AB với A (1; 3; 1), B (-2; 0; 1).
Câu 9. Viết phương trình mặt cầu (S) trong các trường hợp sau:
a. (S) qua A (3; 1; 0), B (5; 5; 0), tâm I thuộc trục Ox
b. (S) có tâm O và tiếp xúc mặt phẳng (a): 16x – 15y – 12z + 75 = 0
c. (S) có tâm I(-1; 2; 0) và có tiếp tuyến là đường thẳng.
Câu 10. Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD. A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’ . Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:
A. 245/108
B. 9/4
C. 64/27
D. 75/32
Câu 11. Trong không gian cho tam giác ABC đều cạnh bằng 2 cố định, M là điểm thỏa mãn điều kiện MA2 + MB2 + MC 2 = 12. Khẳng định nào sau đây đúng?
A. Tập hợp các điểm M là một mặt cầu có bán kính R =
B. Tập hợp các điểm M là một mặt cầu có bán kính R = 2/3
C. Tập hợp các điểm M là một mặt cầu có bán kính R =
D. Tập hợp các điểm M là một mặt cầu có bán kính R = 2/ 9
Câu 12. Trong không gian Oxyz, phương trình mặt phẳng đi qua ba điểm
(0; -1; 2), B(-2; 0; 3) và C (1; 2; 0) là:
A. 7x – 5y – 3z + 1 = 0
B. 7x – 5y – 3z + 11 = 0
C. 5x + 3y + 7z – 17 = 0
D. 5x + 3y + 7z – 11 = 0
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD. A’B’C’D’ có điểm A trùng với gốc tọa độ, B (a; 0; 0), D (0; a; 0), A’ (0; 0; b) với a > 0, b > 0. Gọi M là trung điểm của cạnh CC’. Giả sử a + b = 4, giá trị lớn nhất của thể tích khối tứ diện A’BDM bằng:
A. 64/27
B. 128/27
C. 128/9
D. 27/4
Câu 14. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (0; 0; 0), B(0; 1; 1), C (1; 0 ; 1). Xét điểm D thuộc mặt phẳng Oxy sao cho tứ diện ABCD là một tứ diện đều. Kí hiệu D(x0; y0; z0) là tọa độ của điểm D. Tổng x0 + y0 bằng:
A. 0
B. 1
C. 2
D.3
Câu 15. Viết phương trình mặt phẳng qua A(1; 1; 1) vuông góc với hai mặt phẳng (a): x + y – z -2 = 0, (b): x – y + z = 0
A. y + z – 2 = 0
B. x + y + z -3 = 0
C. x – 2y + z = 0
D. x + z – 2 = 0
