Cách bấm máy tính đạo hàm cực nhanh và chính xác

Bạn đang xem: Cách bấm máy tính đạo hàm cực nhanh và chính xác tại truongptdtntthptdienbiendong.edu.vn

1. Đạo hàm là gì?

Đạo hàm là một khái niệm toán học quan trọng và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế học, khoa học máy tính và nhiều lĩnh vực khác. Đơn giản, đạo hàm là một cách để đo đạc sự biến đổi của một hàm số tại một điểm cụ thể.

Khi chúng ta nói về đạo hàm của một hàm số, chúng ta thường xuyên đề cập đến việc xác định tỷ lệ biến đổi của giá trị của hàm số khi biến số đầu vào thay đổi. Đạo hàm của một hàm số $f (x)$ tại một điểm $x = a$ thường được ký hiệu là $f^{'} (a)$ hoặc

. Nó cho biết tỉ lệ tăng/giảm của hàm số tại điểm đó.

Đạo hàm có thể hiểu đơn giản là đường tiếp tuyến tại một điểm trên đồ thị của hàm số. Nói cách khác, nếu bạn vẽ một đường thẳng chạm vào đồ thị của hàm số tại một điểm cụ thể, đường thẳng đó sẽ có độ dốc bằng với giá trị của đạo hàm tại điểm đó.

Đạo hàm không chỉ giúp chúng ta hiểu về tốc độ biến đổi của một biến số, mà còn có thể áp dụng trong nhiều tình huống thực tế. Ví dụ, trong kinh tế học, đạo hàm được sử dụng để tìm kiếm điểm cực trị của hàm lợi nhuận hoặc để đo lường tỷ lệ biến đổi của các tham số kinh tế.

Trong vật lý, đạo hàm giúp chúng ta tính toán vận tốc, gia tốc, và biểu diễn sự biến đổi của các đại lượng này theo thời gian.

Đạo hàm cũng là cơ sở cho nhiều phép toán phức tạp hơn như tích phân, và nó là một phần quan trọng của lý thuyết tích phân và vi phân. Các khái niệm như đạo hàm riêng, đạo hàm bội, và ứng dụng trong các phương trình vi phân cũng đều dựa trên ý tưởng cơ bản về đạo hàm.

Nói chung, đạo hàm không chỉ là một khái niệm toán học trừu tượng mà còn là một công cụ mạnh mẽ giúp chúng ta hiểu và mô tả sự biến đổi của thế giới xung quanh.

2. Cách bấm máy tính đạo hàm cực nhanh và chính xác:

2.1. Cách bấm máy tính đạo hàm cấp 1:

Bước 1: Bấm tổ hợp phím +

Bước 2: Nhập hàm số tại điểm x₀ và ẩn bằng.

Ví dụ 1: Cho hàm số $y = sqrt {4x - 1}$ . Tính đạo hàm của hàm số tại x = 2

Hướng dẫn giải

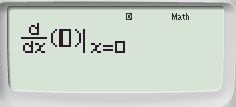
Bước 1: Bấm tổ hợp phím + ta được: Cách bấm máy tính đạo hàm

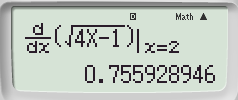
Bước 2: Nhập hàm số $y = sqrt {4x - 1}$ và x = 2 ta được Cách bấm máy tính đạo hàm

Nhấn “=” ta được kết quả cần tìm: 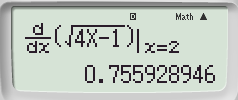Cách bấm máy tính đạo hàm

2.2. Cách bấm máy tính đạo hàm cấp 2:

Công thức tính đạo hàm cấp 2:

$y''left( {{x_0}} right) = mathop {lim }limits_{Delta x to 0} frac{{Delta y'}}{{Delta x}} = frac{{y'left( {{x_0} + 0,000001} right) - y'left( {{x_0}} right)}}{{0,000001}}$

Bước 1: Tính đạo hàm cấp 1 tại x = x₀

Bước 2: Tính đạo hàm cấp 1 tại x = x₀ + 0,000001

Nhập vào máy tính $frac{{Ans - Pr eAns}}{x}$ rồi nhấn “=”

Ví dụ 2: Tính giá trị gần đúng đạo hàm cấp hai của hàm số $y = 4{x^3} + sqrt {x + 1}$ tại x₀ = 3

Hướng dẫn giải

Bước 1: Tính đạo hàm cấp 1 của hàm số tại tại x₀ = 3

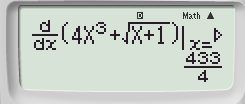
Cách bấm máy tính đạo hàm

Bước 2: Lưu kết quả vừa tìm được vào hàm A

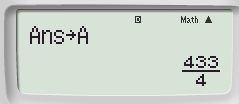
Bấm tổ hợp phím + + ta được: Cách bấm máy tính đạo hàm

Bước 3: Tính đạo hàm cấp 1 của hàm số tại tại x₀ = 3 + 0.000001

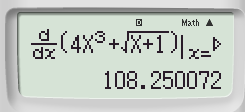
Cách bấm máy tính đạo hàm

Lưu kết quả vào hàm B

Bấm tổ hợp phím + + ta được: Cách bấm máy tính đạo hàm

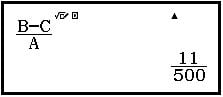
Bước 4: Áp dụng công thức đạo hàm cấp 2 ta có: $y'' = frac{{y'left( {3 + 0.00001} right) - y'left( 3 right)}}{{0.000001}}$

Ta được kết quả: 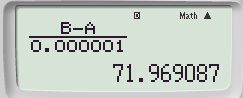Cách bấm máy tính đạo hàm

Dự đoán công thức đạo hàm bậc n:

Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3

Bước 2: Tìm quy luật về dấu, về hệ số, về biến số, về số mũ rồi rút ra công thức tổng quát

3. Cách tính đạo hàm bằng máy Casio Fx-580VN:

3.1. Tổng quan các bước tiến hành:

Để thực hiện cách bấm máy tính đạo hàm nhanh và có kết quả chính xác nhất, bạn cần phải trang bị cho mình các kiến thức nền tảng liên quan đến máy tính Casio. Sau đây, công thức cần nhớ khi thực hiện bấm máy:

– Lệnh bấm tính đạo hàm cấp 1: Nhấn Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Quy trình bấm đạo hàm cấp 1:

+ Bước 1: Nhấn Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

+ Bước 2: Nhập biểu thức $frac{d}{dx}(f(x))x=x0$ và nhấn phím Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

– Tính đạo hàm cấp 2: $y'' (x0)= lim_{Delta zrightarrow 0}frac{Delta y'}{Delta x}=frac{y'(x0+0.000001)-y' (x0)}{0,000001}$

Quy trình bấm đạo hàm cấp 2:

+ Bước 1: Tính đạo hàm tại điểm x=x0

+ Bước 2: Tính đạo hàm cấp 1 tại điểm x=x0+ 0,000001

+ Bước 3: Nhập vào máy tính $frac{Ans-PreAns}{X}$ và nhấn phím Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

* Ví dụ minh họa: tính dạo hàm cấp 1:

Cho hàm số sau: $y=frac{4x+1}{sqrt{x^{2}+2}}$ . Hãy tính đạo hàm của hàm số tại x=3. Hướng dẫn bấm máy như sau:

Bước 1: Nhấn tổ hợp phím Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất ta được

Bước 2: Nhập hàm số và x=3, ta được: Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Bước 3: nhấn phím Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất có kết quả sau:

Vậy kết quả đạo hàm của hàm số là: 0,1370506112

3.2. Các ví dụ minh họa:

* Ví dụ đạo hàm cấp 2:

Hãy tính đạo hàm cấp 2 của hàm số sau:

Tính f”(2) biết $f(x) =frac{x^{2}+2x+3}{5x+7}$ . Sau đây là cách bấm máy tính đạo hàm cấp 2:

Bước 1: gán 10-9 vào biến nhớ A Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Bước 2: Tính f'(A+2) gán vào biến nhớ B

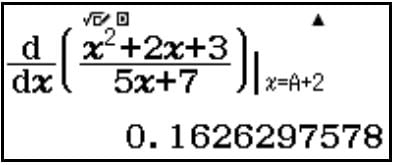
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Bước 3: Tính f’ (2) gán vào biến nhớ

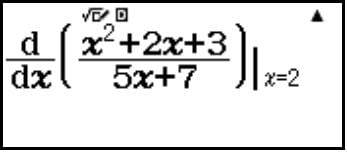
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Bước 4: Tính $frac{B-C}{A}$ . Kết quả của phép tính này là đạo hàm cấp 2 của hàm số.

Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

4. Cách tính đạo hàm cấp 2 trên máy Casio 880 BTG:

4.1. Tổng quan các bước tiến hành:

Ví dụ 1: Tính đạo hàm cấp hai của hàm số f(X)= $frac{x^{5}}{5}-frac{x^{3}}{3}+2$ tại các điểm -1; 0; 1.

– Bước 1: Gán hàm số $frac{x^{5}}{5}-frac{x^{3}}{3}+2$ vào hàm nhớ f(x)

+ Bước 1.1. Nhấn phím FUNCTION => chọn Define f(x)=> nhấn phím OK

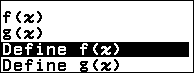
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

+Bước 1.2. Nhập hàm số $frac{x^{5}}{3}-frac{x^{3}}{3}+2$ => nhấm phím EXE

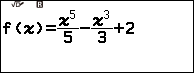
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

– Bước 2: Mở bảng tính Spreadsheet

Nhấn phím HOME => cHỌN Spreadsheet => nhấm phím OK

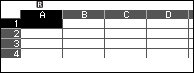
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

– Bước 3: Nhập -1, 0, 1 vào các ô A1, A2, A3

Nhập -1 => nhấn phím EXE => nhập 0=> nhấn phím EXE => nhập 1 => nhấn phím EXE

– Bước 4: Chọn ô B1 rồi sử dụng tính năng Fill Formula với Form là (d/dx(f(x), A1+10^(-9)) – d/dx)(f(x),A1)) $rfloor$ 10^(-9) và Rang là B1:B3

+ Bước 4.1. Chọn ô B1

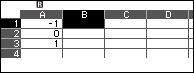
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

+ Bước 4.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK

Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

+ Bước 4.3. Nhập (d/dx(f(x),A1+10^(-9))-s/dx(f(x),A1)) $rfloor$ 10^(-9)=> Nhấn phím EXE => nhập B1:B3 => nhấn phím EXE => nhấn phím

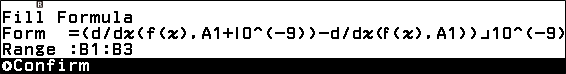
Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Bước 5: Quan sát cột B

Những giá trị ở cột B chính là gái trị gần đúng của đạo hàm cấp 2 của hàm số f(x) tại các điểm ở cột A

Cách bấm máy tính đạo hàm nhanh, chi tiết, chính xác nhất

Vậy đạo hàm cấp 2 của hàm số đã cho tại các điểm -1, 0, 1 lần lượt là -2, 0, 2.

4.2. Cách tính đạo hàm cấp 2 tại nhiều điểm:

Có hai tính năng giúp chúng tra tính nhanh đạo hàm cấp 2 tại nhiều điểm là tính năng bảng tính Spreadsheet và tính năng bảng giá trị Table trên máy tính Casio

Cách 1. Sử dụng tính năng bảng tính Spreadsheet

Bước 1. Gán hàm số cần tính đạo hàm cấp 2 vào hàm nhớ f(x)

Bước 2. Mở bảng tính Spreadsheet

Bước 3: Nhập các điểm cần tính đạo hàm cấp hai vào các ô A1, A2, A3..

Bước 4. Chọn ô B1 rồi sử dụng tính năng Fill Formula với Form là (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1)) $rfloor$ 10^(-9) và Rang là B1:Bn

Chú ý: n là bao nhiêu phụ thuộc vào số lượng điểm cần tính các bạn nhé.

Bước 5. Quan sát cột B: Những giá trị ở cột B chính là giá trị gần đúng của đạo hàm cấp 2 của hàm số f(x) tại các điểm ở cột A.

Cách 2. Sử dụng tính năng bảng giá trị Table

Bước 1. Mở tính năng tạo bảng giá trị Table

Bước 2. Nhập f(X) là $frac{frac{d}{dx}(f(x))left |frac{}{}x=x+10^{9}-frac{d}{dx}(f(x)) right |x=x}{10^{-9}}$

Bước 3. Giữ nguyên các giá trị Start =1, End=5, Step=1

Bước 4. Nhập các giá trị cần tính đạo hàm cấp hai vào cột x

* Những lưu ý khi bấm đạo hàm trên máy tính Casio 880

– Khi sử dụng hàm lương giác f(x), hãy chỉ định Radian làm Angle Unit trên menu SETTINGS

– Giá trị tol nhỏ hơn cho độ chính xác cao hơn nhưng cũng làm mất nhiều thời gian tính toán. Khi chỉ định tol, hãy sử dụng giá trị từ 1 x 10-22 trở lên.

– Kết quả có thể không chính xác hoặc bị cáo lỗi nếu:

+ Các điểm không kế tiếp trong các giá trị x

+ Sự thay đổi đột ngột trong các giá trị x

+ Bao hàm điểm cực đại và điểm cực tiểu trong các giá trị x

+ Bao hàm điểm uốn trong các giá trị x

+ Bao hàm các điểm không vi phân được trong giá trị x

+ Kết quả phép tính vi phân gần bằng 0

+ Tính năng Derivative(d/dx) không khả dụng trng các ứng dụng số phức Complex, hệ cơ số Base-N và hộp toán học Math Box.