Là một trong những dạng toán quan trọng của lớp 8, để chuẩn bị cho kì thi tuyển sinh từ lớp 9 lên lớp 10, công thức đáng nhớ 7 được các thầy cô giảng dạy cho các em học sinh. Vậy hằng đẳng thức đáng nhớ là gì và tại sao nó lại quan trọng như vậy?
Dưới đây, đội ĐẢO NGƯỢC giới thiệu công thức 7 hằng đẳng thức đáng nhớ và cách vận dụng công thức này vào bài tập cụ thể, kèm ví dụ minh họa cho từng dạng toán để các em dễ dàng nắm bắt.
Mục lục bài viết [Ẩn]

một hằng số đáng nhớ là gì? Ý nghĩa của hằng đẳng thức đáng nhớ là gì?
Một hằng đẳng thức đáng nhớ là một loạt các phương trình liên quan kết hợp với nhau để tạo thành một đẳng thức. Trong môn toán, mỗi học sinh bắt buộc phải biết 7 hằng đẳng thức đáng nhớ được quy định để có thể vận dụng vào giải toán.
Khi nhớ được 7 hằng đẳng thức đồng nghĩa với việc các em sẽ nắm được bản chất, tiết kiệm thời gian và hạn chế sai sót khi giải toán. Ngoài ra, những kiến thức này còn rèn luyện cho bạn những kỹ năng mềm như sự khéo léo, cẩn thận cũng như thúc đẩy niềm đam mê với môn học.

7 Đẳng Thức Đáng Nhớ

Đầu tiên. Công thức bình phương của tổng (A + B)²
Định nghĩa: Bình phương của tổng (A + B)² sẽ bằng bình phương của số thứ nhất A² cộng với hai lần tích của số thứ nhất và thứ hai 2AB, sau đó cộng với bình phương của số thứ hai B².
Công thức bình phương của một tổng: (A + B)² = A² + 2AB + B
*Ví dụ bài 16 trang 11 SGK toán 8:

Ví dụ:
a) Tính ( a + 3 )2.
b) Viết biểu thức x2+ 4x + 4 là bình phương của một tổng.
Dạy:
a) Ta có: ( a + 3 )2= một2+ 2.a.3 + 32 = một2 + 6a+9.
b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
2. Công thức bình phương của một sự khác biệt (A – B)²
Định nghĩa: Bình phương của hiệu (A – B)² sẽ bằng bình phương của số thứ nhất A² trừ đi hai lần tích của số thứ nhất và thứ hai 2AB, sau đó cộng với bình phương của số thứ hai B².
Công thức bình phương cho sự khác biệt: (A – B)² = A² – 2AB + B
Ví dụ Bài 16 trang 1 SGK Toán 8:

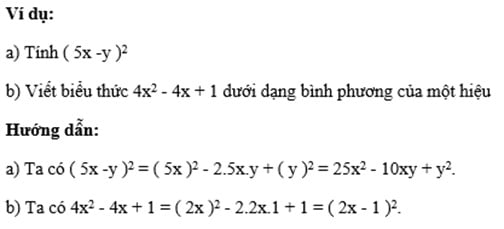
3. Công thức tính hiệu của hai bình phương MỘT –
Định nghĩa: Hiệu của hai bình phương của hai số A² – B² sẽ bằng hiệu của hai số A – B đó nhân với tổng của hai số A + B đó.
Công thức tính hiệu của hai bình phương: A² – B² = (A – B)(A + B)

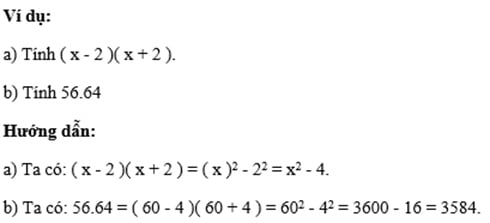
4. Công thức lập phương của một tổng (A + B)³
Định nghĩa: Lập phương của tổng hai số (A + B)3 sẽ bằng lập phương của số đầu tiên A3 cộng ba lần tích bình phương của số thứ nhất nhân với 3A thứ hai2B, cộng ba lần tích của số thứ nhất nhân bình phương của số thứ hai 3AB2rồi cộng lập phương của số thứ hai B3.
Công thức lập phương của một tổng: (A + B)3 = Một3 + 3A2B +3AB2 + BỎ3

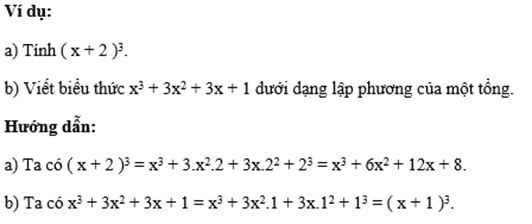
5. Công thức lập phương của một sự khác biệt (A – B)3
Định nghĩa: Lập phương của hiệu của hai số (A – B)3 sẽ bằng lập phương của số đầu tiên A3 trừ ba lần tích bình phương của số thứ nhất nhân với 3A thứ hai2B, cộng ba lần tích của số thứ nhất nhân bình phương của số thứ hai 3AB2rồi trừ lập phương của số thứ hai B3.
Công thức lập phương của một sự khác biệt: (A – B)3 = Một3 – 3A2B +3AB2 – DI DỜI3

Ví dụ:
a) Tính ( 2x – 1 )3.
b) Viết biểu thức x3– 3x2y + 3xy2– y3 như khối lập phương của một sự khác biệt.
Dạy:
a) Ta có: ( 2x – 1 )3
= ( 2 lần )3 – 3.( 2x )2.1 + 3( 2x ).12 – Đầu tiên3
= 8x3 – 12 lần2 + 6x – 1
b) Ta có: x3– 3 lần2y + 3xy2– y3
= ( x )3 – 3.x2.y + 3.x. y2 – y3
= ( x – y )3
6. Công thức tổng của hai lập phương MỘT3 + BỎ3
Định nghĩa: Tổng hai lập phương của hai số A3 + BỎ3 sẽ là tổng của số thứ nhất cộng với số thứ hai A + B, sau đó nhân với bình phương còn thiếu của tổng của số thứ nhất và thứ hai A2 -AB + QUÁ2.
Công thức tính tổng hai lập phương: MỘT3 + BỎ3 = (A + B)(A2 -AB + QUÁ2)
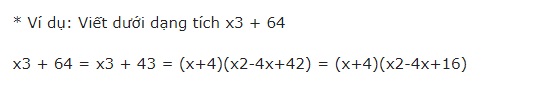
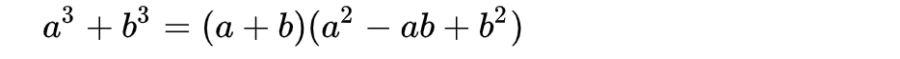
Ví dụ:
a) Tính 33+ 43.
b) Viết biểu thức ( x + 1 )( x2– x + 1 ) là tổng của hai lập phương.
Dạy:
a) Ta có: 33+ 43= ( 3 + 4 )( 32 – 3,4 + 42 ) = 7.13 = 91.
b) Ta có: ( x + 1 )( x2– x + 1 ) = x3+ 13 = x3 + 1.
7. Công thức tính hiệu của hai hình lập phương MỘT3 – DI DỜI3
Định nghĩa: Hiệu của lập phương của hai số sẽ bằng hiệu của số thứ nhất trừ đi số thứ hai A – B, sau đó nhân với bình phương còn thiếu của tổng của số thứ nhất và số thứ hai A2 +AB + QUÁ2.
Công thức cho sự khác biệt của hai khối lập phương: MỘT3 – DI DỜI3 = (A – B)(A2 +AB + QUÁ2)

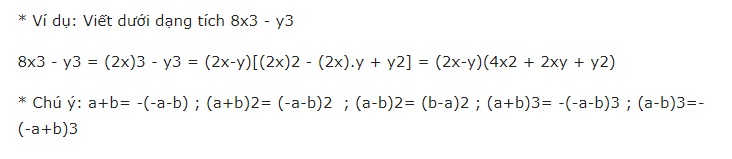
Ví dụ:
a) Tính 63– 43.
b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) là hiệu của hai hình lập phương
Dạy:
a) Ta có: 63– 43= ( 6 – 4 )( 62 + 6.4 + 42 ) = 2,76 = 152.
b) Ta có : ( x – 2y )( x2+ 2xy + 4y2) = ( x )3 – ( 2 năm )3 = x3 – 8 tuổi3.
Hệ quả của 7 hằng đẳng thức đáng nhớ mà bạn cần biết
Bên cạnh bảy hằng đẳng thức đáng nhớ, chúng ta có bảy hệ quả, hoặc các công thức đẳng thức mở rộng của chúng, như sau:
Hệ quả với hằng đẳng thức cấp 2
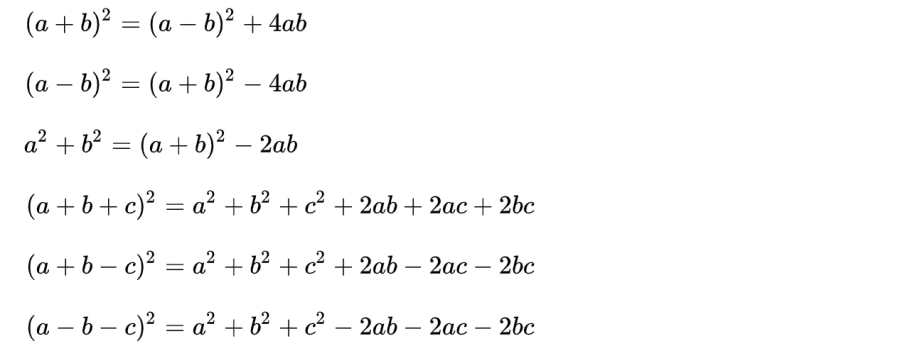
Hệ quả với hằng đẳng thức cấp 3
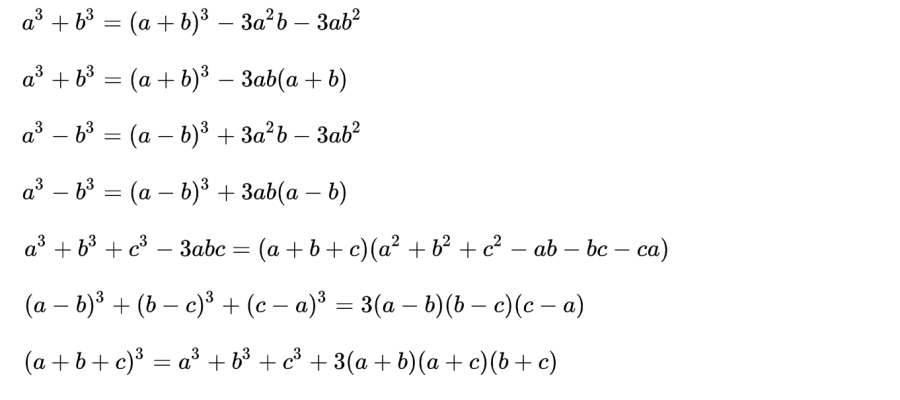
hậu quả chung
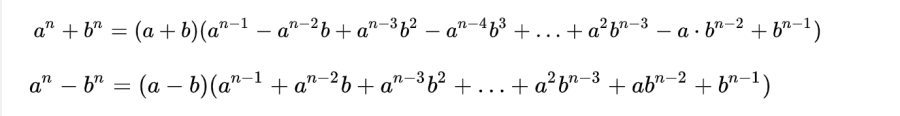
Một số hệ quả khác của hằng đẳng thức
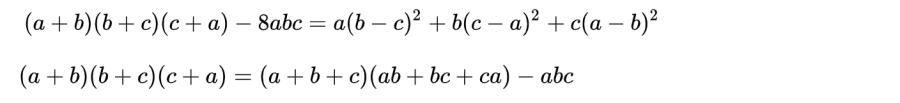
Một số bài tập về 7 hằng đẳng thức đáng nhớ (9 dạng)

1. Bài tập 7 hằng đẳng thức đáng nhớ có lời giải
Dạng 1: Tính giá trị của biểu thức
Câu hỏi: Tính giá trị của biểu thức:
![]()
Phần thưởng
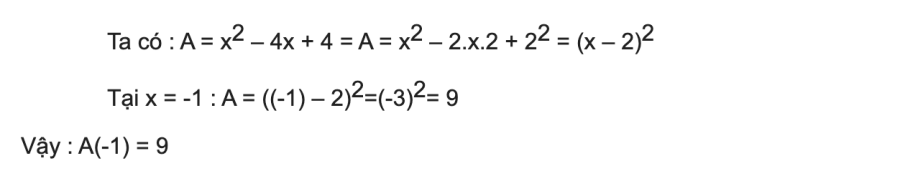
Dạng 2: Chứng minh đẳng thức
Câu hỏi: Hãy chứng minh đẳng thức:
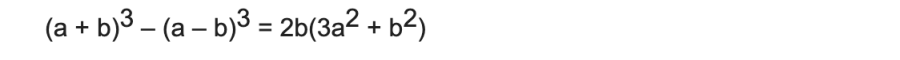
Phần thưởng
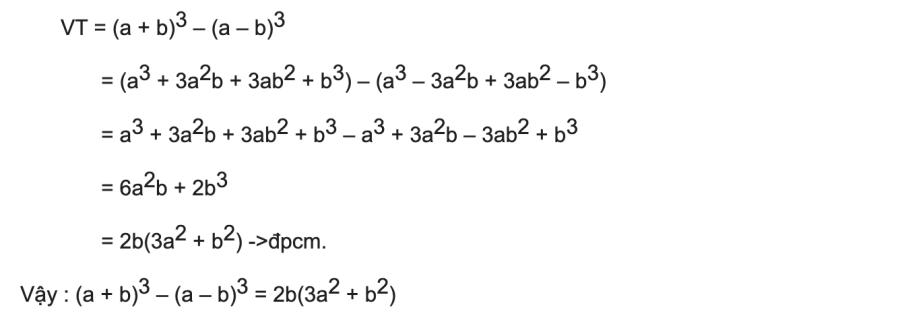
Dạng 3: Chứng minh bất đẳng thức
Biến đổi bất phương trình về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến hình để đưa A về 1 trong 7 hằng đẳng thức.
Dạng 4: Tìm giá trị nhỏ nhất của biểu thức
Chủ thể: Tìm giá trị nhỏ nhất của biểu thức:

Phần thưởng
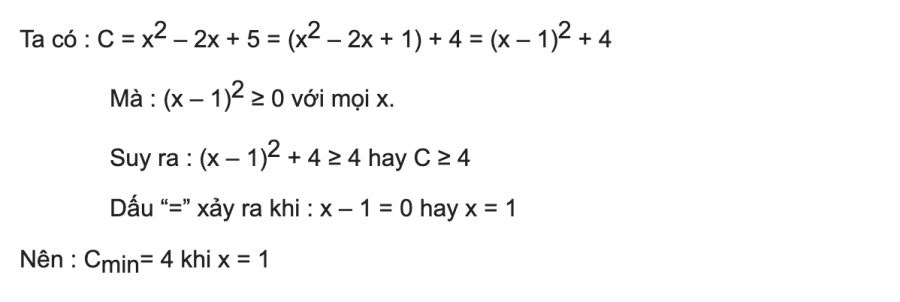
Dạng 5: Tìm giá trị lớn nhất của biểu thức
Câu hỏi: Tìm giá trị lớn nhất của biểu thức:
![]()
Phần thưởng
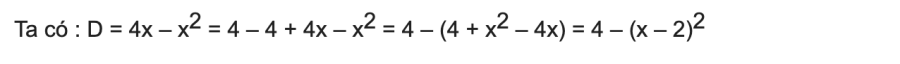
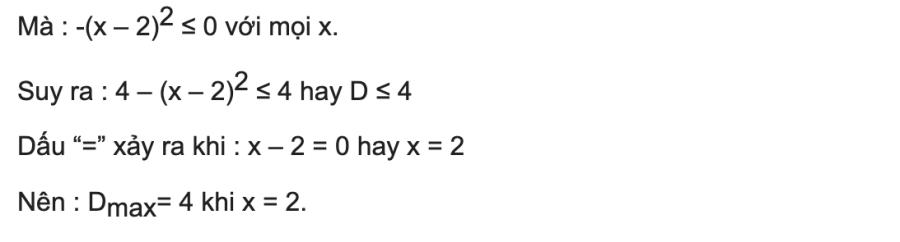
Dạng 6: Chứng minh biểu thức A không phụ thuộc biến
Đề bài: Chứng minh rằng biểu thức A không phụ thuộc vào biến:
![]()
Phần thưởng

Dạng 7: Tìm x.
Đề bài: Tìm x biết:
![]()
Phần thưởng
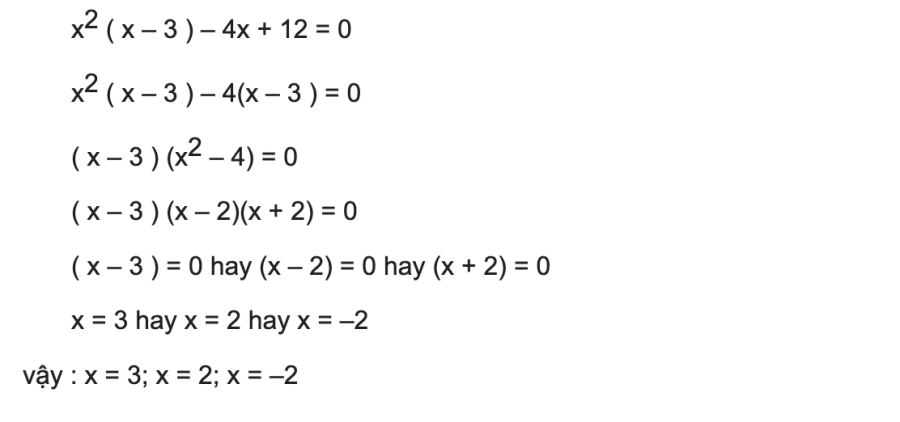
Dạng 8: Phân tích đa thức
Câu hỏi: Tìm nhân tử của đa thức:
![]()
Phần thưởng

Dạng 9: Thực hiện phép tính phân số
Đề bài: Em hãy làm phép tính phân số
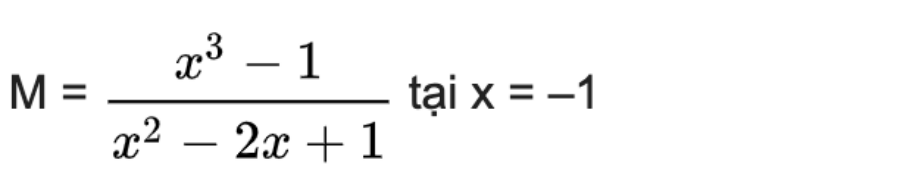
Phần thưởng
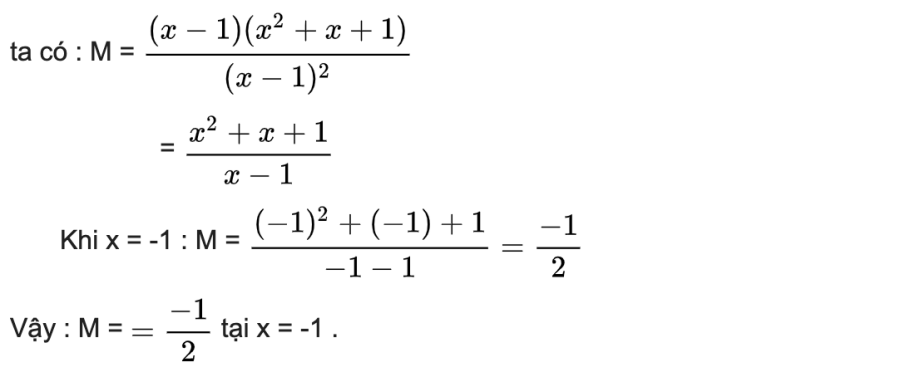
2. Bài tập 7 hằng đẳng thức đáng nhớ không lời giải
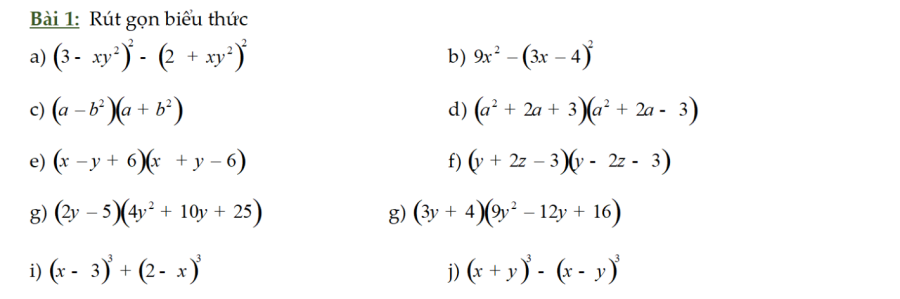
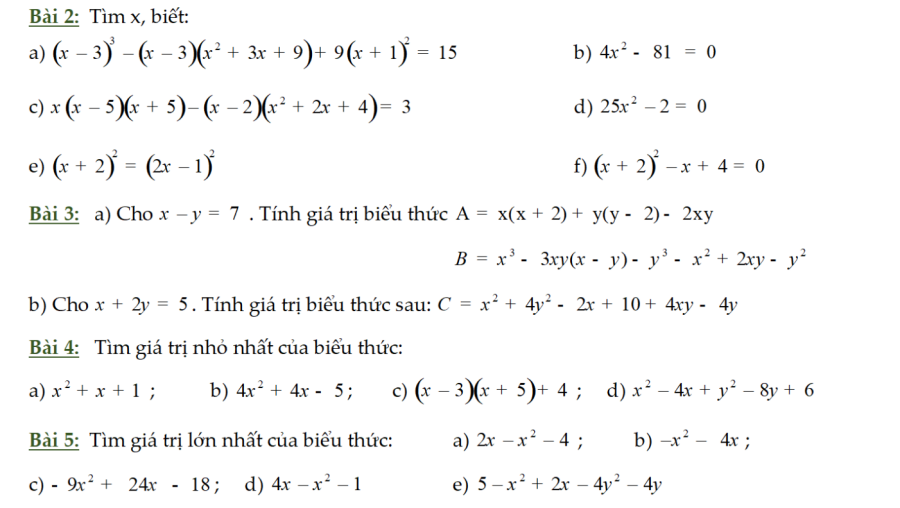
Trên đây là Phương trình đáng nhớ 7 công thức và bài tập về chúng mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này các em có thể biết đầy đủ 7 hằng đẳng thức đáng nhớ cũng như áp dụng giải bài toán dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%

