Diện tích hình nón Đó là một trong những kiến thức toán học quan trọng trong chương trình THCS. Tuy nhiên đến nay nhiều bạn vẫn chưa biết diện tích hình nón là gì và cách tính diện tích hình nón như thế nào?
Tại đây, đội ĐẢO NGƯỢC hướng dẫn bạn cách tính diện tích hình nón Đơn giản, chi tiết, dễ hiểu qua bài viết sau.
Mục lục bài viết [Ẩn]

Hình nón là gì? Diện tích hình nón là gì?
hình nón trong hình học không gian là hình khi quay tam giác vuông quanh trục của nó (1 cạnh góc vuông) 1 vòng ta được hình trụ nón.
Diện tích hình nón được đề cập với 2 khái niệm: xung quanh và toàn phần.
- khu vực xung quanh nón là phần chỉ gồm diện tích xung quanh, bao quanh nón, không kể diện tích đáy.
- Toàn bộ khu vực Hình nón được tính bằng độ lớn của toàn bộ không gian chiếm bởi hình, bao gồm cả diện tích xung quanh và diện tích của đáy hình tròn.
*Các loại nón
Tùy theo đỉnh thẳng hay nghiêng mà nón được chia thành 3 loại:
- hình nón: Có 2 đường tròn song song
- hình nón tròn: Có một đỉnh vuông góc với mặt đáy của tâm đường tròn
- Hình nón xiên: Có một đỉnh không được vẽ vuông góc với tâm của đường tròn, nhưng có thể được vẽ từ bất kỳ điểm nào không phải là tâm của đường tròn cơ sở.
* Tính chất của hình nón
Hình nón có các tính chất chính sau:
- Không có cạnh
- Có 1 đỉnh tam giác
- Có một mặt tròn gọi là đáy
*Chiều cao (h): khoảng cách từ tâm đường tròn đến đỉnh của hình nón, hình tạo bởi đường cao và bán kính trong của hình nón sẽ là một tam giác vuông.
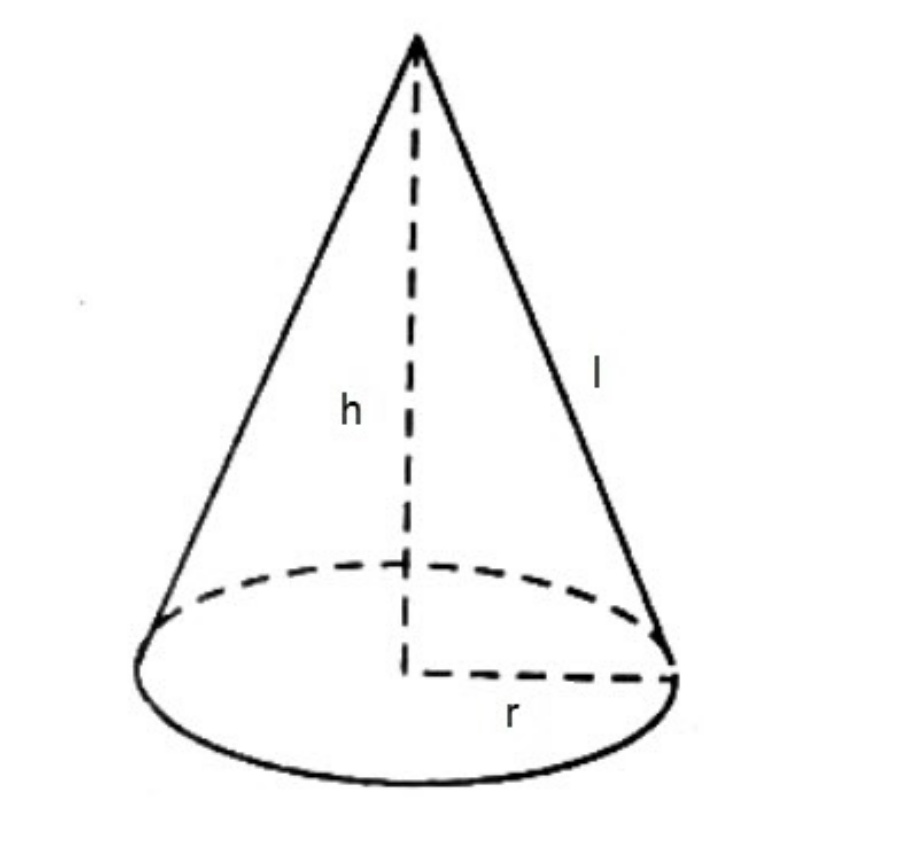
Công thức diện tích hình nón
1. Công thức tính diện tích hình nón đều
Diện tích xung quanh hình nón được tính bằng tích của hằng số Pi (π) nhân với bán kính đáy của hình nón (r) nhân với đường sinh hình nón (l). Trong đó, đường sinh có thể là đường thẳng hoặc cong phẳng (có độ dài từ mép hình tròn đến đỉnh hình nón).
Công thức:
Sxq = . r. tôi
Trong đó:
- Sxq: Diện tích xung quanh hình nón.
- : Hằng số Pi có giá trị gần đúng là 3,14 .
- r: Bán kính đáy của hình nón bằng đường kính chia cho 2 (r = d/2).
- tôi: Đường sinh của hình nón.
Tổng diện tích hình nón được tính bằng diện tích xung quanh hình nón cộng với diện tích đáy của hình nón. Vì diện tích đáy là hình tròn nên công thức tính diện tích hình tròn là Sđ = π. rr
Công thức:
Stp = Sxq + Sd = π. r. tôi + . r2
Trong đó:
- tiêu chuẩn: Diện tích toàn phần của hình nón.
- : Hằng số Pi có giá trị gần đúng là 3,14 .
- r: Bán kính đáy của hình nón bằng đường kính chia cho 2 (r = d/2).
- tôi: Đường sinh của hình nón.
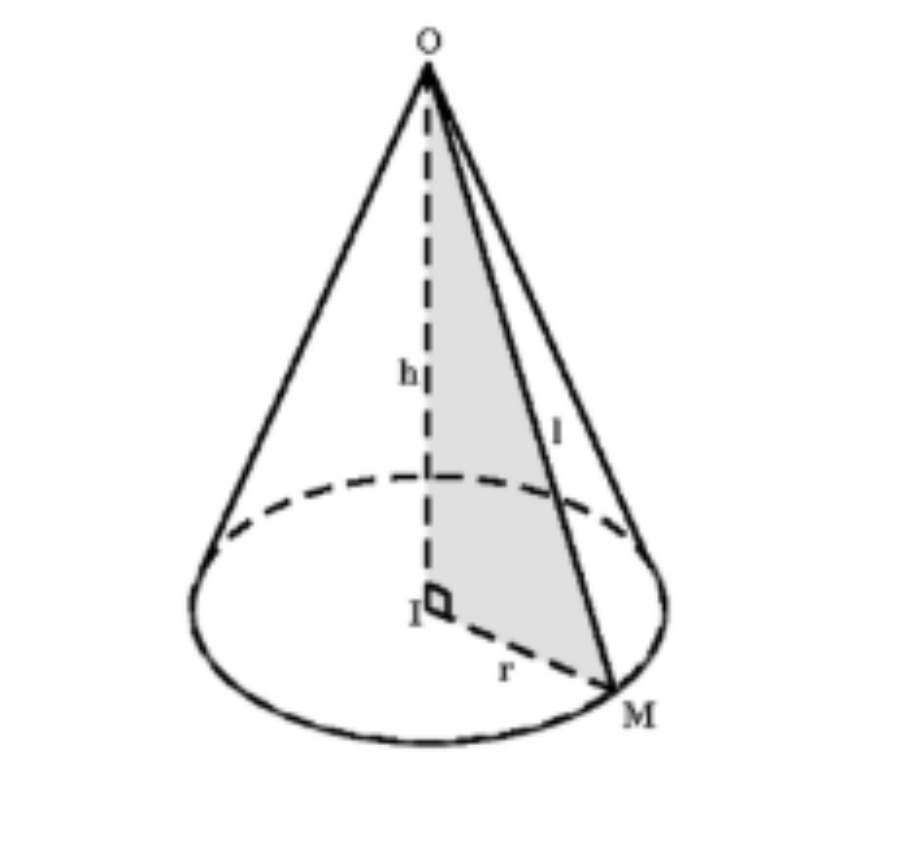
2. Công thức tính diện tích hình nón cụt
Diện tích xung quanh hình nón cụt gồm diện tích của mặt xung quanh hình nón cụt, không kể diện tích của hai đáy và được tính bằng hiệu diện tích xung quanh của hình nón lớn và hình nón nhỏ.
Công thức:
Sxq = . (r1 + r2) . tôi
Trong đó:
- Sxq: Khu vực xung quanh hình nón cụt.
- r1, r2: Bán kính 2 đáy của hình nón cụt.
- tôi: Độ dài đường sinh của hình nón cụt.
Tổng diện tích hình nón cụt là độ lớn của toàn bộ không gian hình chiếm, bao gồm diện tích xung quanh và diện tích của hai đáy tròn, và được tính bằng diện tích xung quanh cộng với diện tích của hai đáy.
Công thức:
Stp = Sxq + S2đáy
Có nguồn gốc từ:
Stp = . (r1 + r2) . l + π . r21 + . r22
Trong đó:
- Sxq: Khu vực xung quanh hình nón cụt.
- tiêu chuẩn: Tổng diện tích hình nón cụt
- S2day: Diện tích 2 cạnh đáy
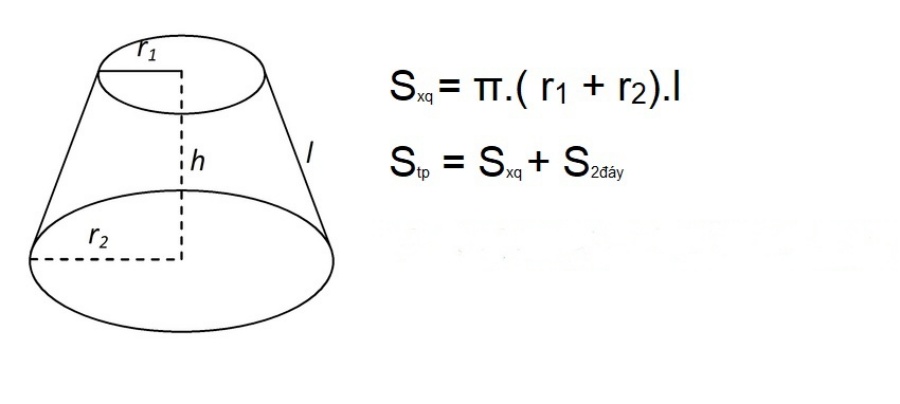
Hướng dẫn cách tính diện tích hình nón
Bước 1: Viết công thức tính diện tích xung quanh hình nón
Đầu tiên, bạn ghi diện tích toàn phần của hình nón ra giấy để tiện tính toán.
Công thức tính diện tích toàn phần hình nón = x bán kính x cạnh + x bán kính2 = xrxs + r2
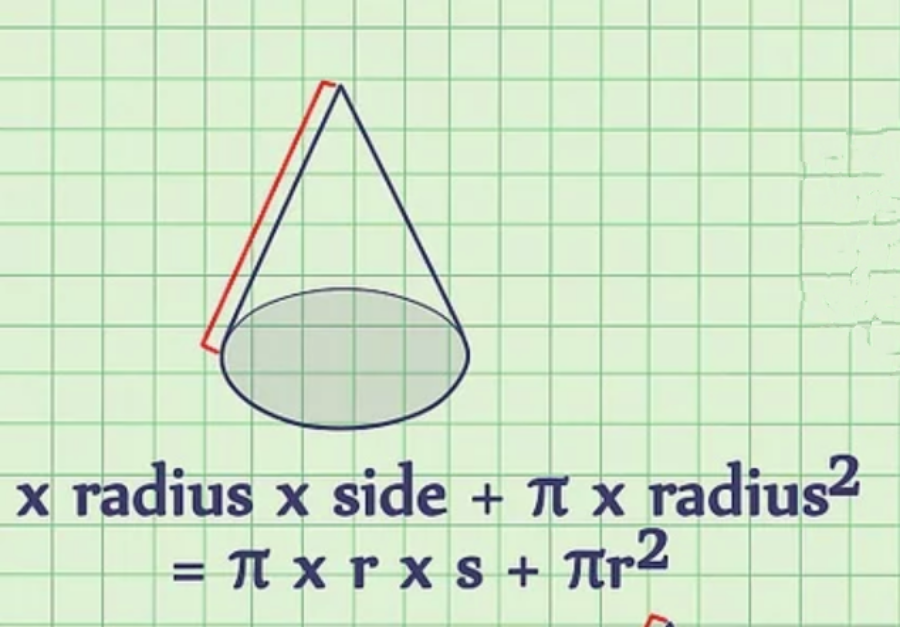
Bước 2: Ghi kích thước của hình nón
Sau đó bạn tiến hành ghi các kích thước của hình nón ra giấy
Ví dụ: Cho một hình nón có r = 2 in, h = 4 in

Bước 3: Tính diện tích xung quanh hình nón
Tại đây, bạn thay các kích thước của hình nón để tính diện tích hình nón. Đây là cách thực hiện:
Ví dụ: Diện tích mặt nón = (2 x 4) + x 22 = 37,7 inch2
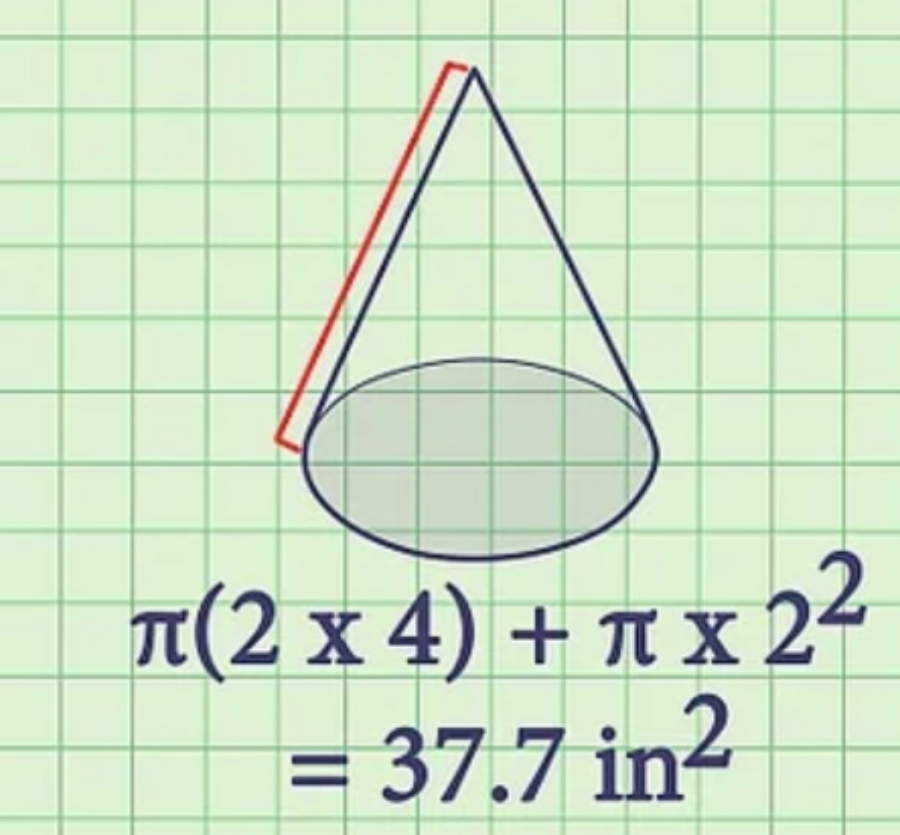
Một số bài tập tính diện tích hình nón
1. Bài tập tính diện tích hình nón có lời giải
Câu 1: Cho hình nón có chiều cao bằng 6 cm, đường sinh bằng 10 cm. Tính toán:
a) Diện tích xung quanh của hình nón
b) Diện tích toàn phần của hình nón.
Phần thưởng:
a) Cho hình nón có đỉnh O, tâm đáy H, các điểm A, B thuộc đường tròn đáy.
Ta có: OA là đường sinh = 10 cm, OH là đường cao = 6 cm.
Xét tam giác vuông OHA (ngay tại H):
Theo định lý Pitago ta có: HA = √(OA2 – OH2) = √(102 – 62) = √64 = 8 (cm)
=> HA là bán kính đáy của hình nón.
Diện tích xung quanh của hình nón là: 8 x 10 x = 80π (cm2)
b) Diện tích toàn phần của hình nón là: = 8π x (10 + 8) = 144π (cm2)
Câu 2: Cho một hình nón có bán kính đáy là 3cm và chiều cao của hình nón là 7cm. Tính diện tích toàn phần của hình nón.
Phần thưởng:
Công thức đường sinh là l = (h2 + r2) = (72 + 32) = 7,9333 cm.
Diện tích toàn phần của hình nón là: Stp = π.r(l + r) = 3,14 . 3 . (7,9333 + 3) = 102,988cm2.
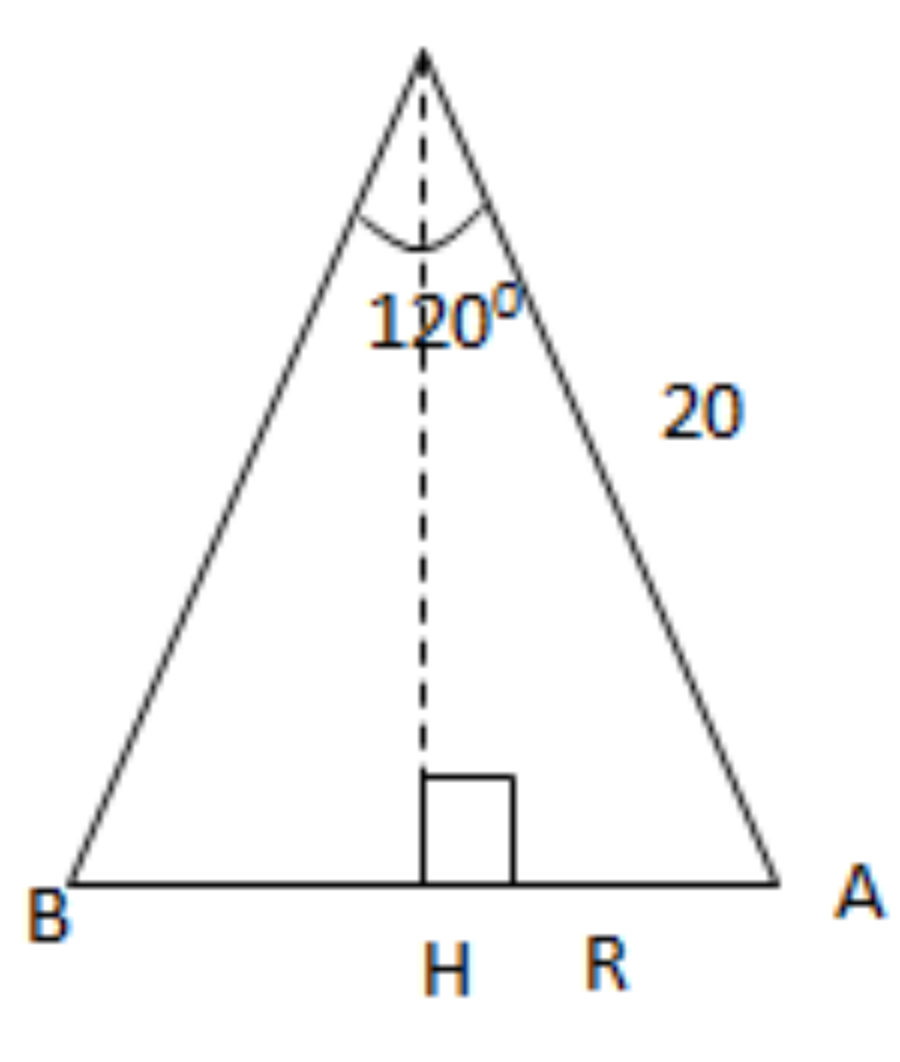
Câu 3: Xét một hình nón có góc ở đỉnh là 120 .0 Chiều dài của ống sinh là 20 (cm). Tính toán
a) Sxq
b) Đứng
Phần thưởng
a) Cho hình nón có đỉnh là O và tâm đáy là H .
Kí hiệu của đáy là AB
Góc AOB = 120° Góc AOH = 60°, OA = 20
Trong tam giác OHA:
R = HA = OA. sin góc AOH = 20. sin60° = 20. (√3/2) = 10. 3
Sxq = . R. tôi = . 10√3 . 20 = 200√3π (cm2)
b) Stp = π . R. tôi + R2 = 200√3π + 300π = 100(2√3+3)π (cm2)
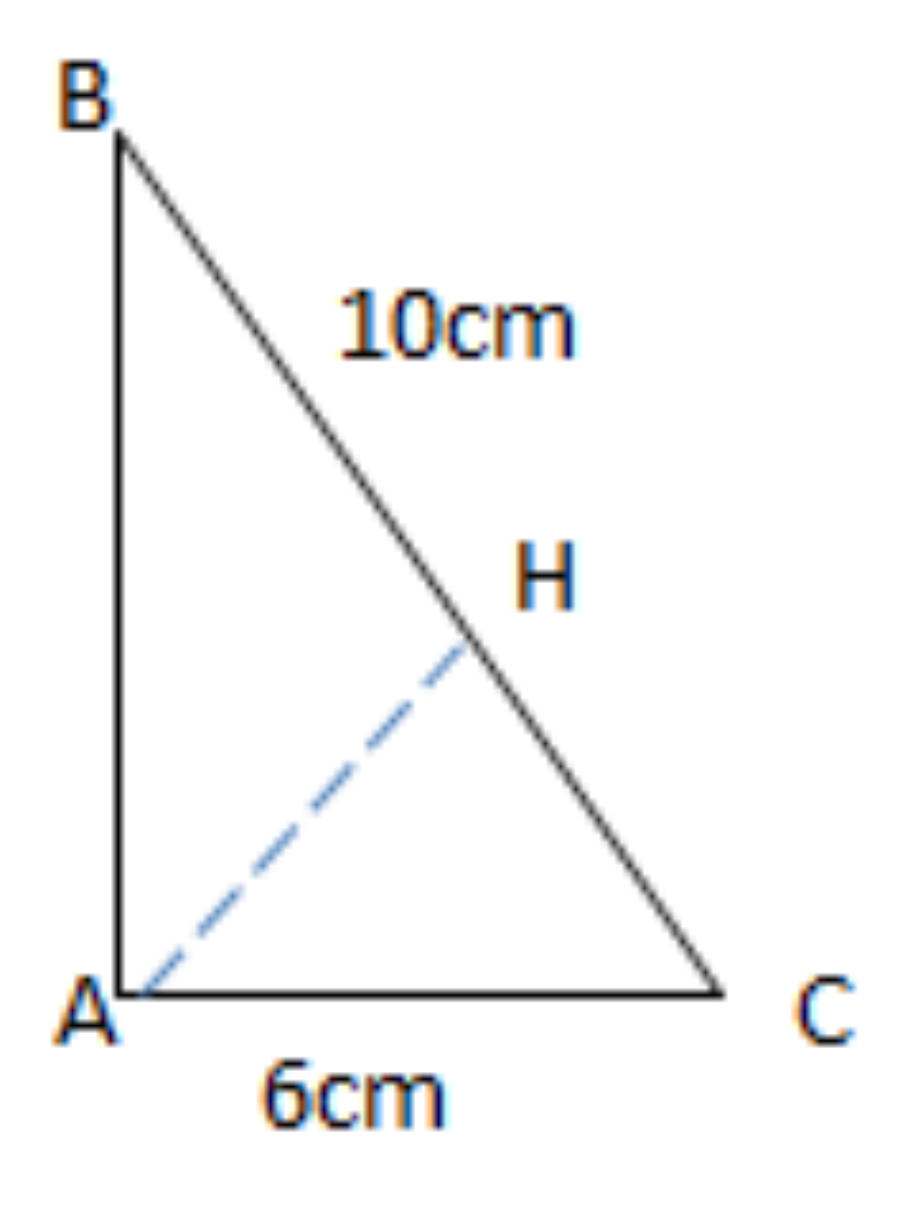
Câu 4: Cho tam giác ABC vuông tại A, AC = 6 (cm), BC = 10 (cm). Cho đường gấp khúc BAC quay quanh BC ta được đường tròn xoay. Tính diện tích xung quanh của hình tròn.
Phần thưởng:
Vẽ AH ⊥ BC tại H. Diện tích xung quanh của hình tròn tạo thành là tổng diện tích xung quanh của hai hình nón.
Hình nón đầu tiên được tạo thành bằng cách cắt đường cong BAH xung quanh BH, R1 = AH, l1 = AB.
SXp1 = π . RẺ2Đầu tiên . l1 = .AH2 . AB
Hình nón thứ hai được tạo thành khi quay hình nón ACH quanh CH, R2 = AH, l2 = AC
SXp2 = π . R22 . l2 = . AH2 . AB
Sxp = Sxp1 + Sxp2 = π . AH2 (AB+AC)
Trong tam giác ABC.
AB2 = TCN2 – AC2 = 102 − 62 = 82
1/ À2 = 1/AB2 + 1/máy lạnh2 = (AB2 + Máy lạnh2) / (AB2 . AC2) = (82 + 62) / (số 82 . 62) = 52 / 242
Sxq = . (24)2 52. (6 + 8) = 8064/25(cm2)
Câu 5: (15/117/Thứ hai SGK)

Câu 6: (16/117/T2 SGK)

Phần thưởng:
Câu 7: (17/117/Thứ hai SGK)
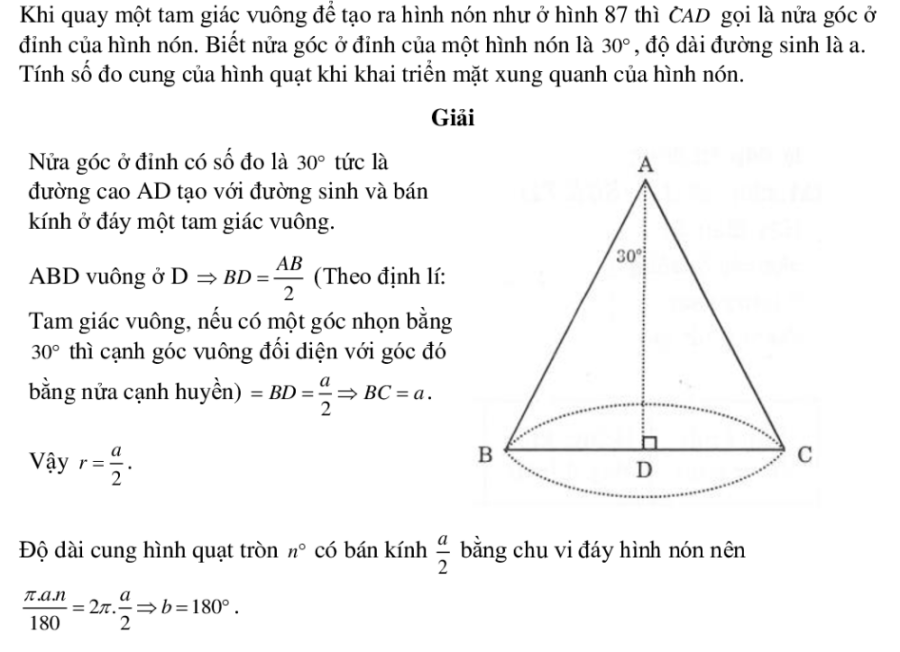
Câu 8: (21/117/T2 SGK)

Câu 9: (22/117/T2 SGK)

Câu 10: (23/117/T2 SGK)
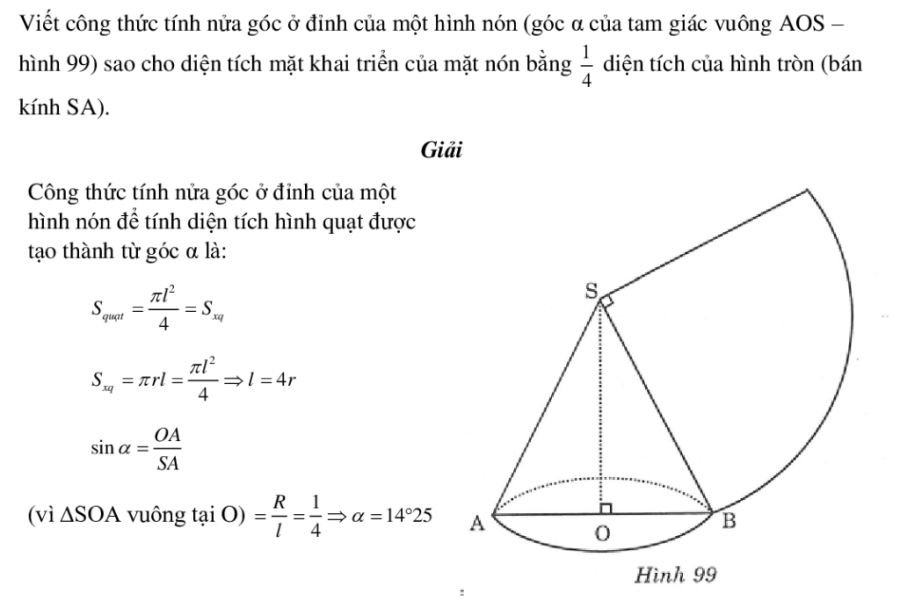
2. Tính diện tích hình nón không có nghiệm
Câu hỏi 1: Xét một hình nón có bán kính đáy 4a và chiều cao 3a. Tính đường sinh, chu vi, diện tích toàn phần, thể tích của khối nón trên.
Câu 2: Cho một hình nón có đường sinh l, góc giữa đường sinh và mặt phẳng đáy là 30º. Tính chu vi hình nón
Câu 3: Một hình nón có thể tích 30 π, nếu giữ nguyên chiều cao và tăng bán kính lên 2 lần thì thể tích của khối nón mới là bao nhiêu?
Câu 4: Cho một hình nón tròn xoay có đỉnh là S; O là tâm đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Tính chu vi hình nón và thể tích khối nón lần lượt?
Câu 5: Một hình nón có đường kính đáy là 2a√3 và góc ở đỉnh là 120 .0. Tính thể tích khối nón đó theo a.
Câu 6: Một hình nón có đường sinh là 2a và diện tích xung quanh là 2πa2 . Thể tích của khối nón là bao nhiêu?
Câu 7: Xét một hình nón có bán kính đáy R = 3(cm) và chiều cao h = 4(cm). Diện tích xung quanh của hình nón là bao nhiêu?
Câu 8: Cho hình nón có chiều cao h = 10cm và thể tích V = 1000π (cm3). Tính diện tích toàn phần của hình nón:
Câu 9: Cho hình thang ABDC vuông tại A và B, biết cạnh AB = BC = 3m, AD = 5m. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB
Câu 10: Cho hình thang vuông cân đối ABCD tại A và B, biết cạnh AB = BC = 4,5 cm, AD = 7,5 cm. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB
Trên đây là Công thức diện tích hình nón & tính toán diện tích hình nón đơn giản, nhanh chóng mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này các bạn hoàn toàn có thể tính được diện tích Hình Nón một cách dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%
thẻ:
khu vực xung quanh hình nóndiện tích đáy của hình nóncông thức hình nóndiện tích hình nón cụt

