Diện tích tam giác là một trong những kiến thức quan trọng theo suốt các bạn học sinh từ lớp 5 đến lớp 12, trong đó đặc biệt là kỳ thi lớp 10. Vậy hình Tam Giác là gì và cách tính diện tích của nó ra sao?
Ngay sau đây, đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn biết hình tam giác là gì, công thức tính diện tích hình tam giác & cách sử dụng nó vô cùng chi tiết, dễ hiểu thông qua bài viết sau.
Mục lục bài viết [Ẩn]
I. Hình tam giác là gì? Diện tích hình tam giác là gì?
Hình Tam giác là hình 2 chiều phẳng có 3 đỉnh là 3 điểm không thẳng hàng và 3 cạnh là 3 đoạn thẳng nối các đỉnh với nhau. Ngoài ra, tam giác còn là đa giác có số cạnh ít nhất (3 cạnh) và luôn luôn là 1 đa giác đơn cũng như luôn là 1 đa giác lồi (các góc trong luôn nhỏ hơn 180°).
Ký hiệu của 1 tam giác có các cạnh AB, BC, AC:
![]()

Các loại tam giác
– Theo độ dài các cạnh:
- Tam giác thường là tam giác có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.
- Tam giác cân là tam giác có 2 cạnh bên và 2 góc ở đáy bằng nhau.
- Tam giác đều là trường hợp đặc biệt của tam giác cân có cả 3 cạnh bằng nhau, 3 góc bằng nhau và bằng 60°.
– Theo số đo các góc trong
- Tam giác vuông là tam giác có 1 góc bằng 90° (là góc vuông).
- Tam giác tù là tam giác có 1 góc trong > 90° (1 góc tù) hay có 1 góc ngoài < 90° (1 góc nhọn).
- Tam giác nhọn là tam giác có 3 góc trong đều < 90° (3 góc nhọn) hay có tất cả góc ngoài > 90° (6 góc tù)
- Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân, 2 cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45°.

Tính chất của tam giác
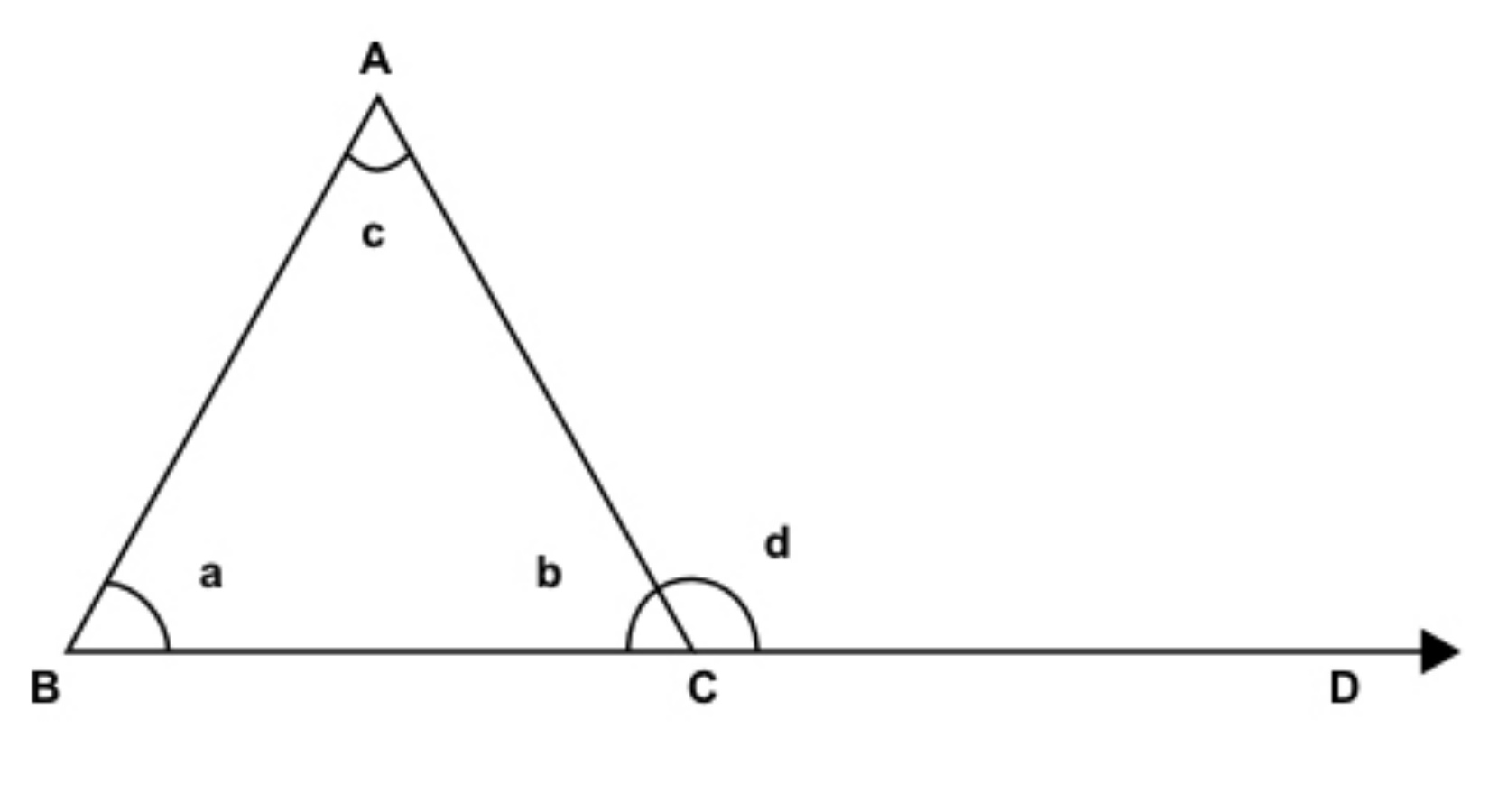
- Tổng các góc trong của một tam giác bằng 180°
- Trong tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn và ngược lại.
- Trọng tâm của tam giác là điểm giao nhau của 3 đường trung tuyến.
- Tâm đường tròn nội tiếp của tam giác là điểm giao nhau của 3 đường phân giác.
- Tâm đường tròn ngoại tiếp của tam giác là điểm giao nhau của 3 đường trung trực
- Tỷ lệ giữa độ dài của mỗi cạnh trong tam giác với sin của góc đối diện là như nhau cho cả 3 cạnh.
- Đường phân giác trong tam giác của 1 góc chia cạnh đối diện thành 2 đoạn thẳng tỷ lệ với 2 cạnh kề 2 đoạn thẳng đó.
- Hiệu độ dài của hai cạnh tam giác sẽ nhỏ hơn độ dài mỗi cạnh và nhỏ hơn tổng độ dài hai cạnh.
- Trực tâm của tam giác là điểm giao nhau của 3 đường cao
- Bình phương độ dài 1 cạnh = tổng bình phương độ dài 2 cạnh còn lại trừ đi 2 lần tích của độ dài 2 cạnh ấy với cosin của góc xen giữa 2 cạnh đó.
- Trong tam giác, đoạn thẳng nối trung điểm 2 cạnh được gọi là đường trung bình.
II. Công thức tính diện tích hình tam giác
1. Công thức tính diện tích tam giác thường
Diện tích tam giác thường bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.
Công thức chung:
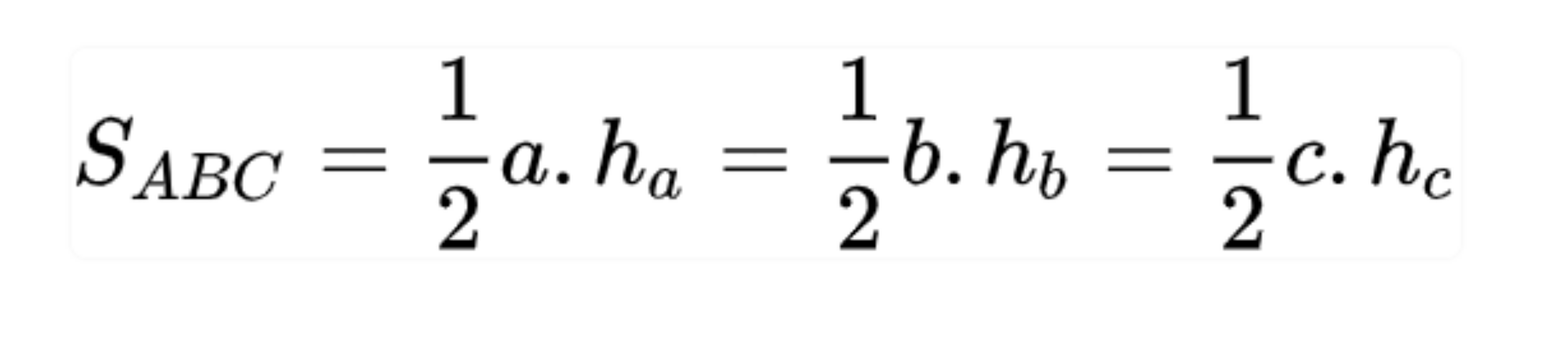
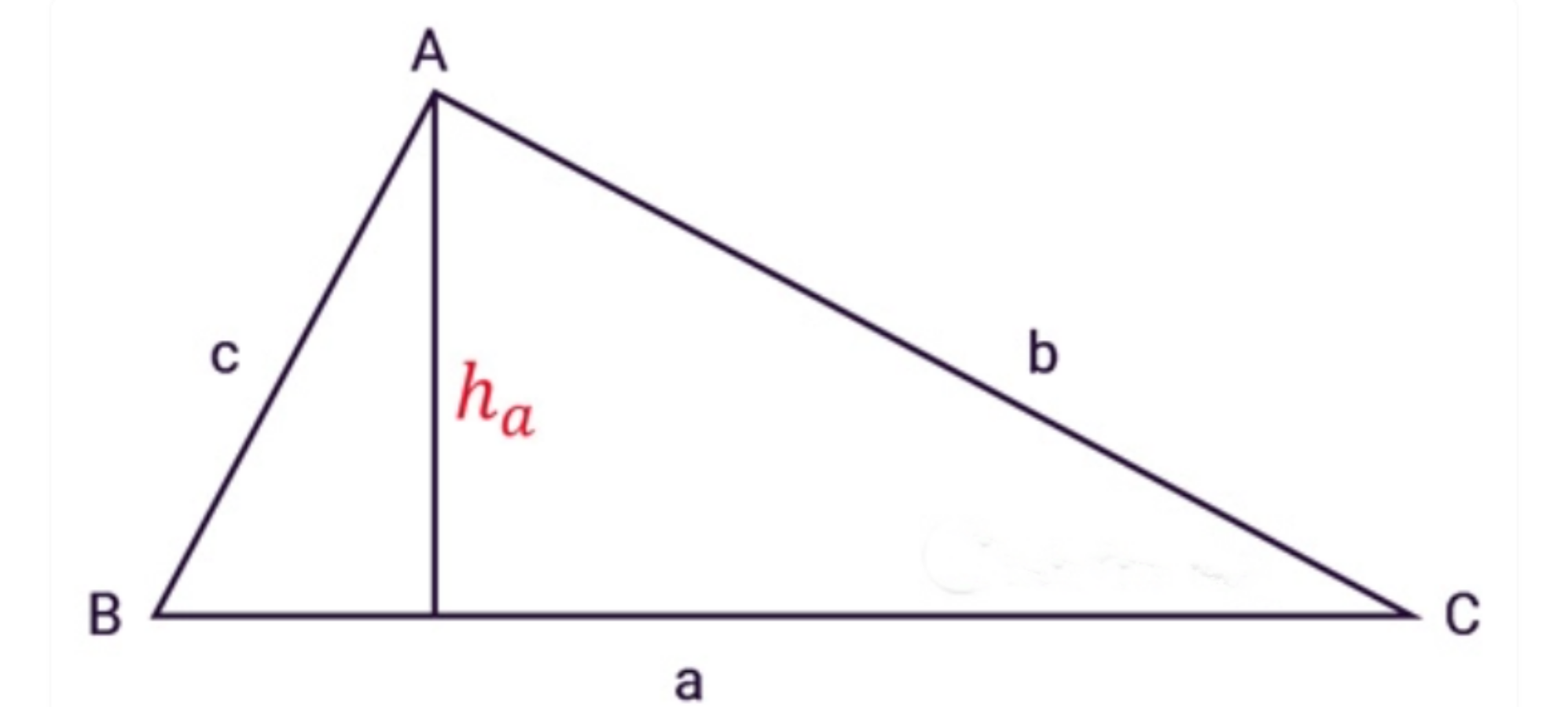
Tính diện tích tam giác khi biết 1 góc sẽ bằng ½ tích 2 cạnh kề với sin của góc hợp bởi 2 cạnh đó trong tam giác.
Công thức:
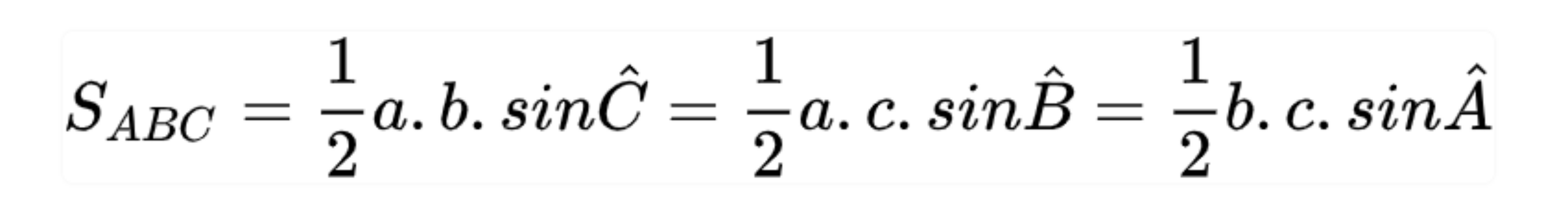
Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
Sử dụng công thức Heron đã được chứng minh:
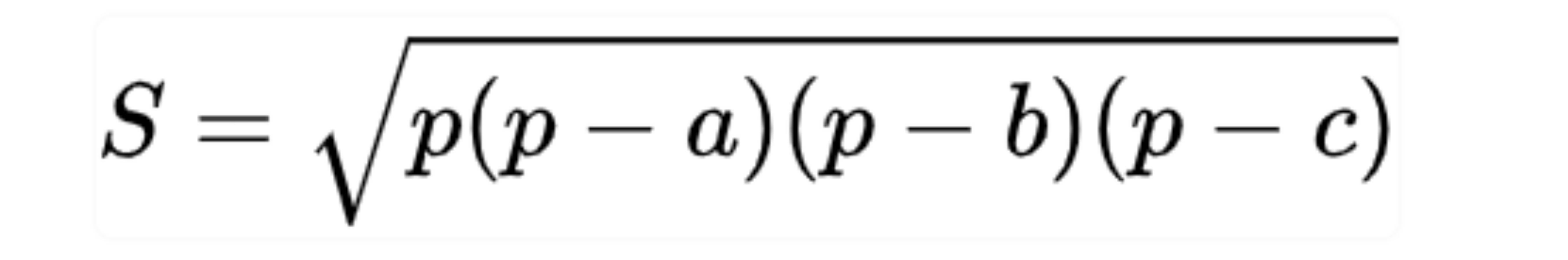
Với p là nửa chu vi tam giác:
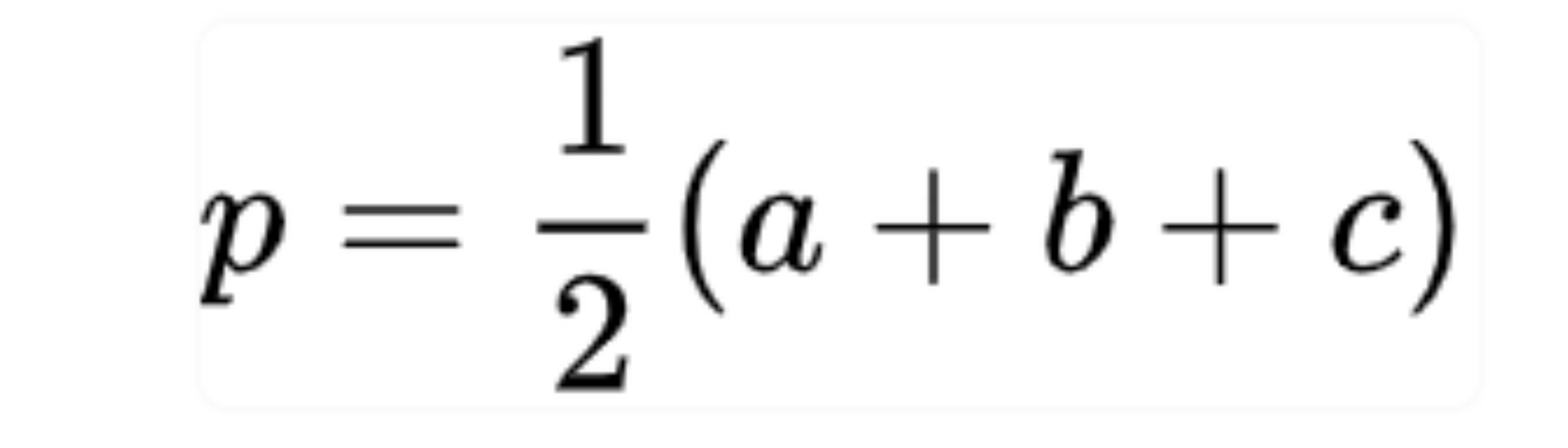
Công thức viết lại:
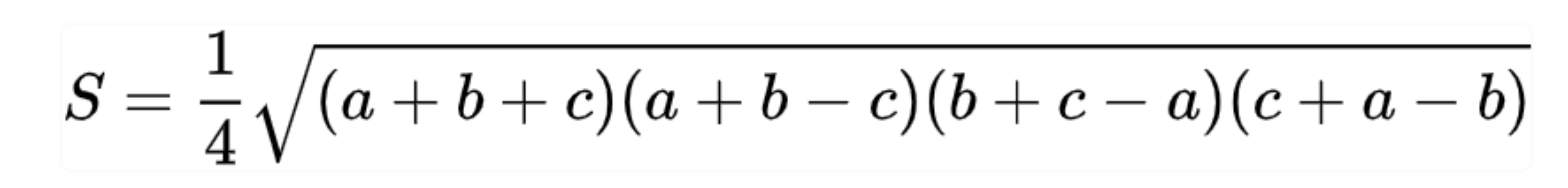
Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).
![]()
Chú ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.
Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r).
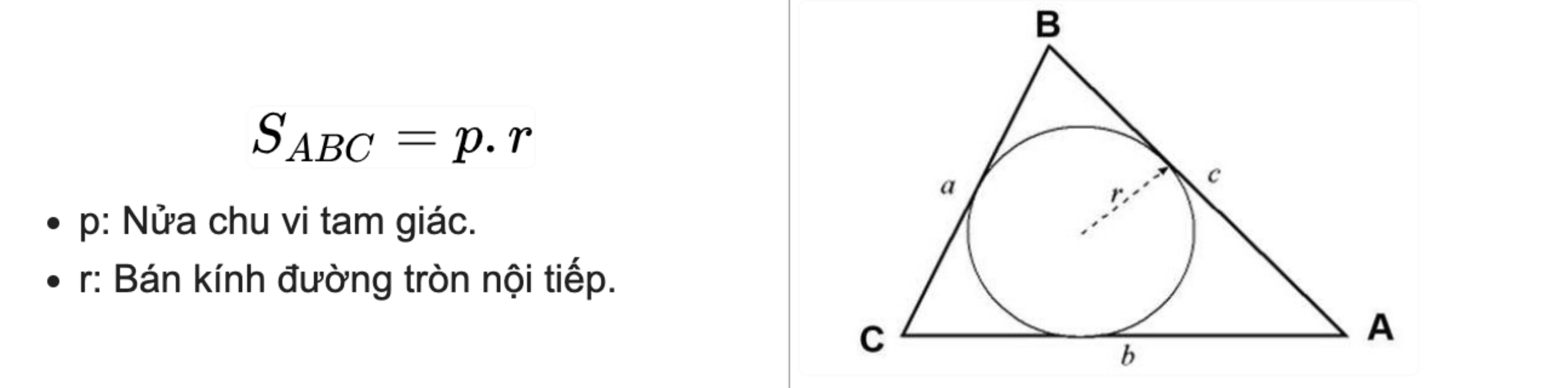
2. Công thức tính diện tích tam giác cân
Từ công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân:
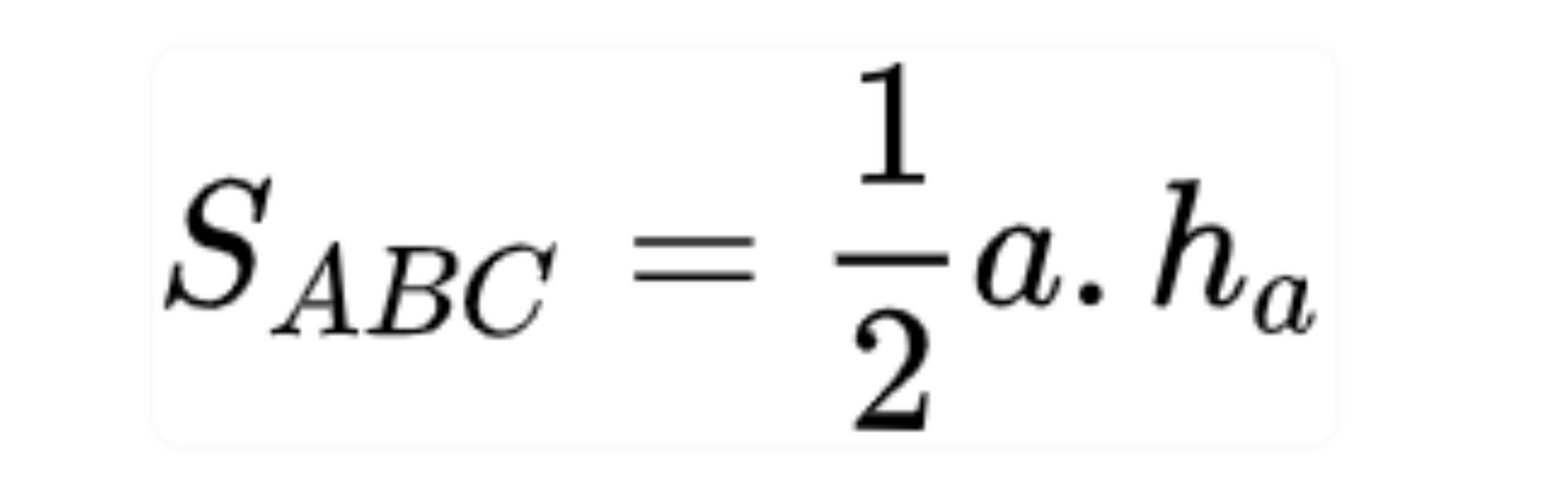
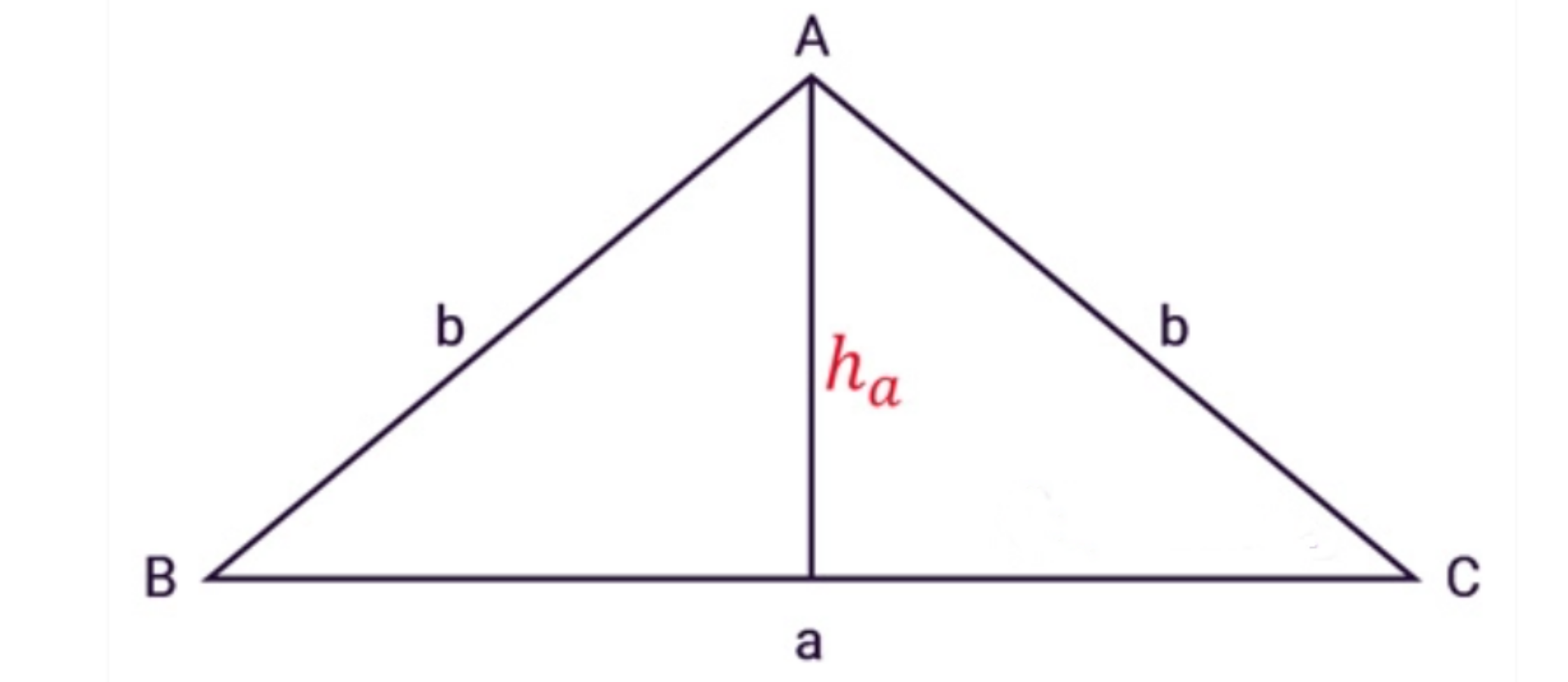
3. Công thức tính diện tích tam giác đều
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh. Áp dụng định lý Heron để suy ra công thức tính diện tích tam giác đều:
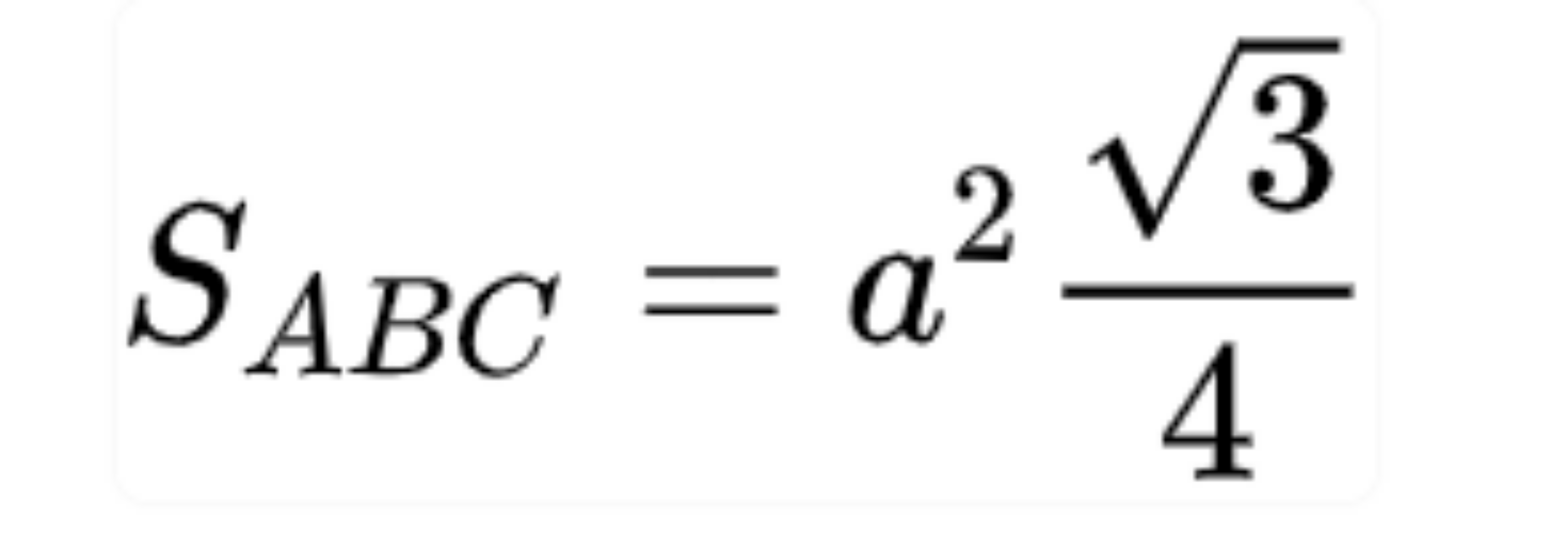
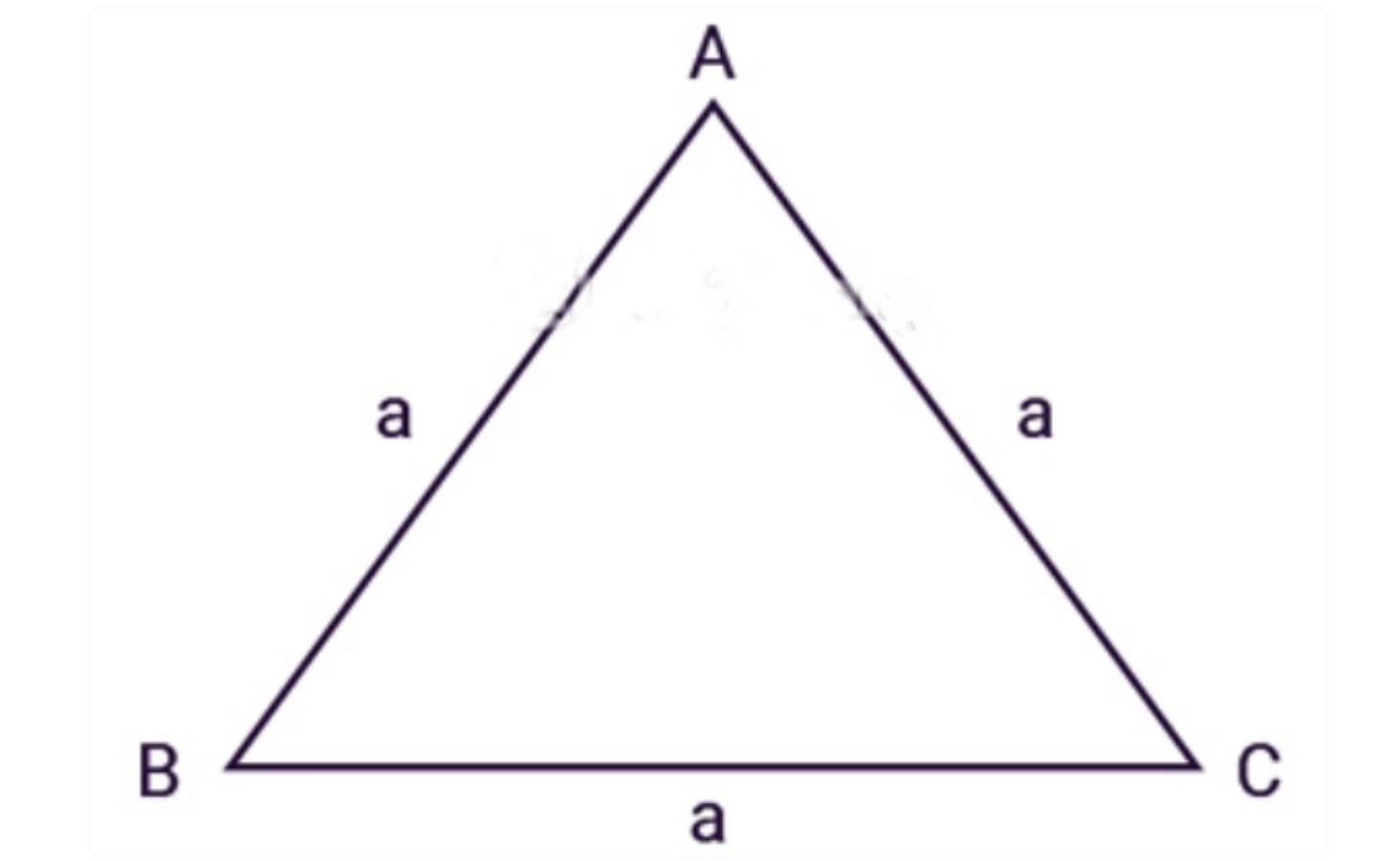
4. Công thức tính diện tích tam giác vuông
Tam giác ABC vuông tại B, a, b là độ dài 2 cạnh góc vuông:
Công thức tính diện tích tam giác vuông:
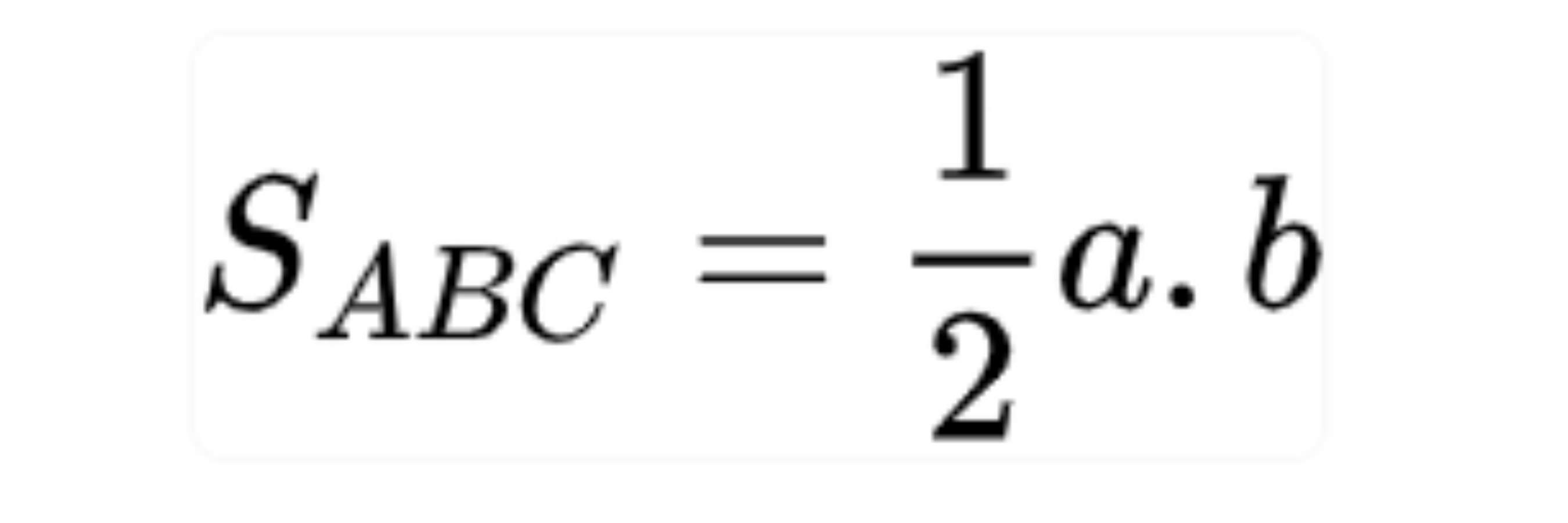
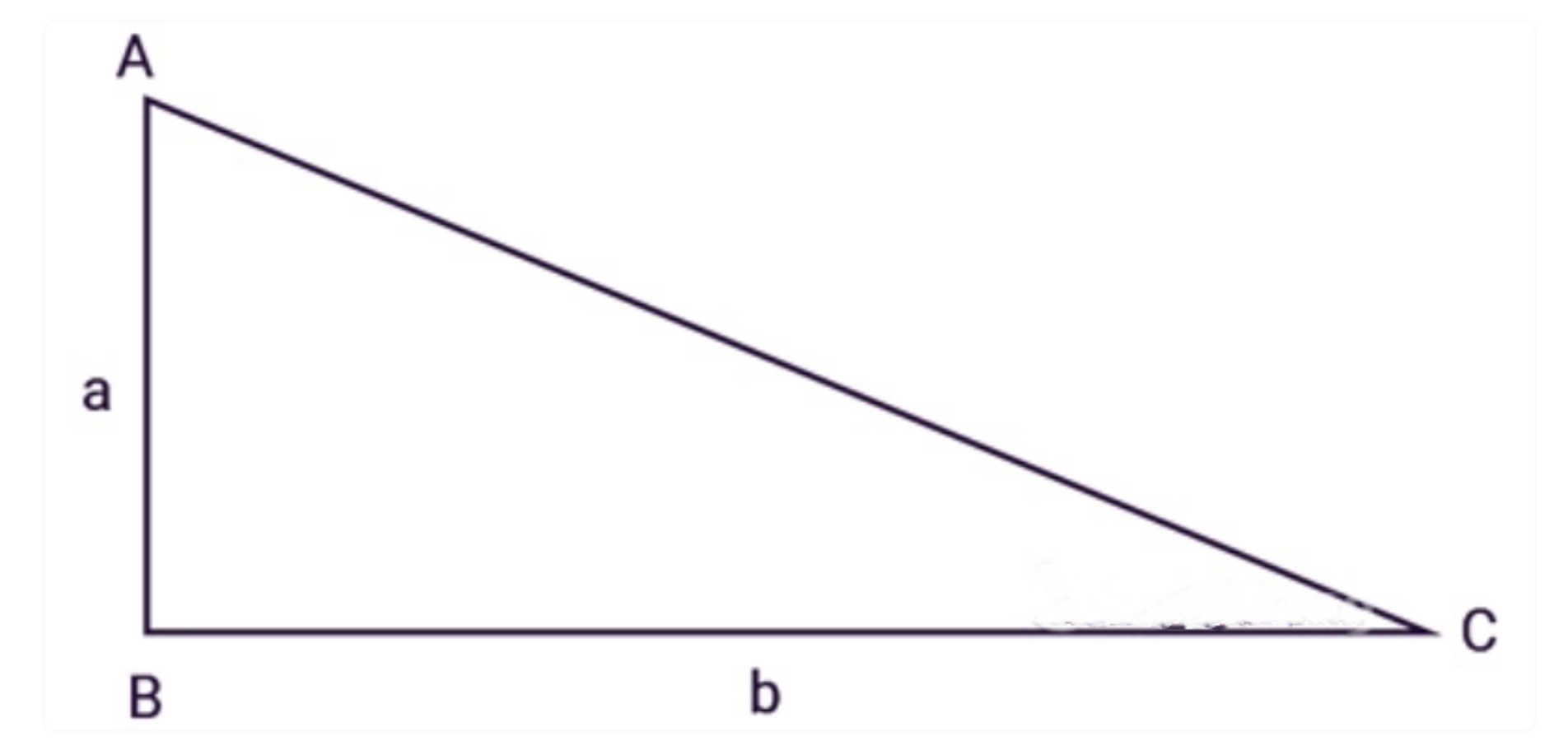
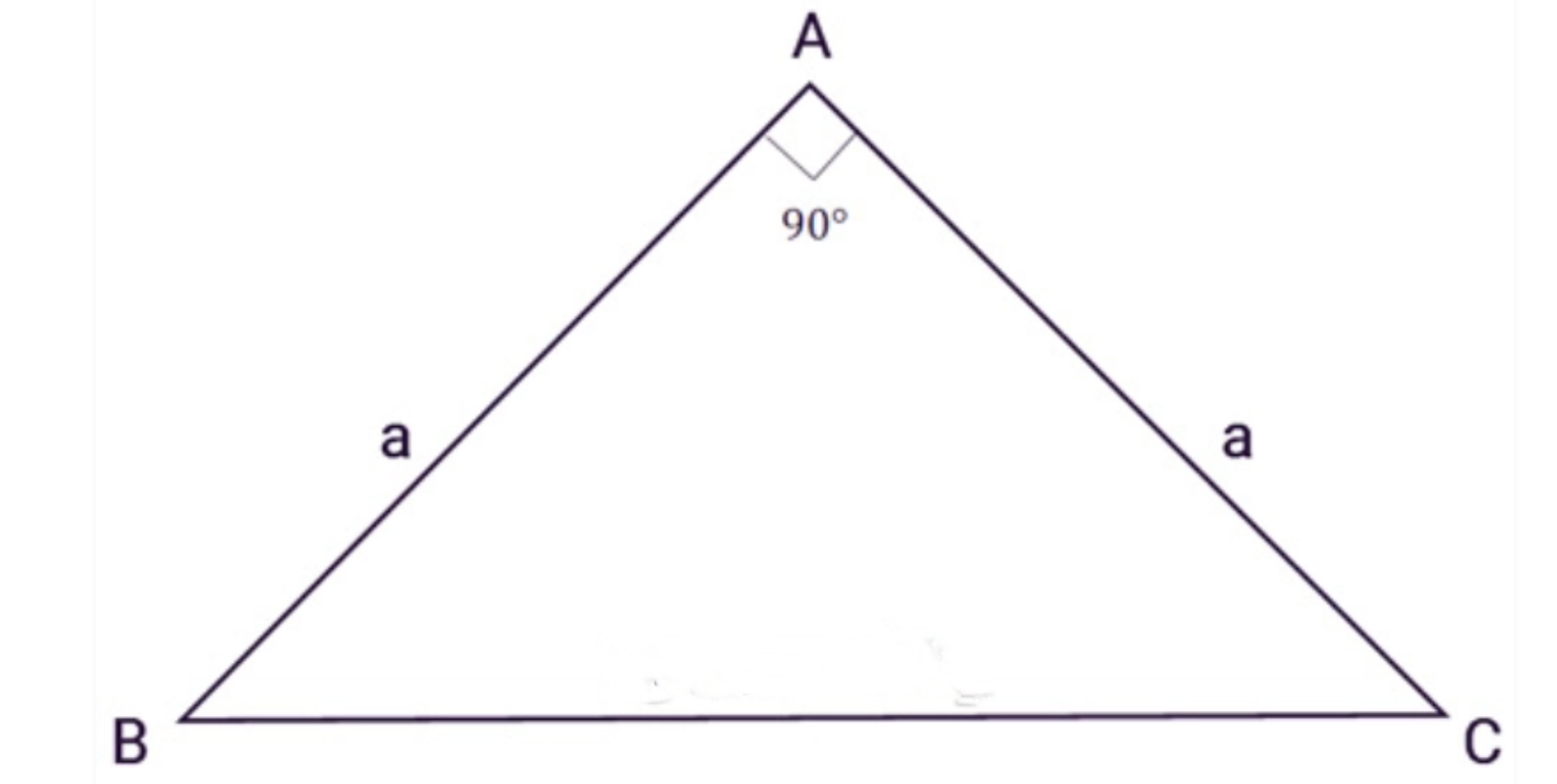
5. Công thức tính diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài 2 cạnh góc vuông
Công thức tính tam giác vuông cân
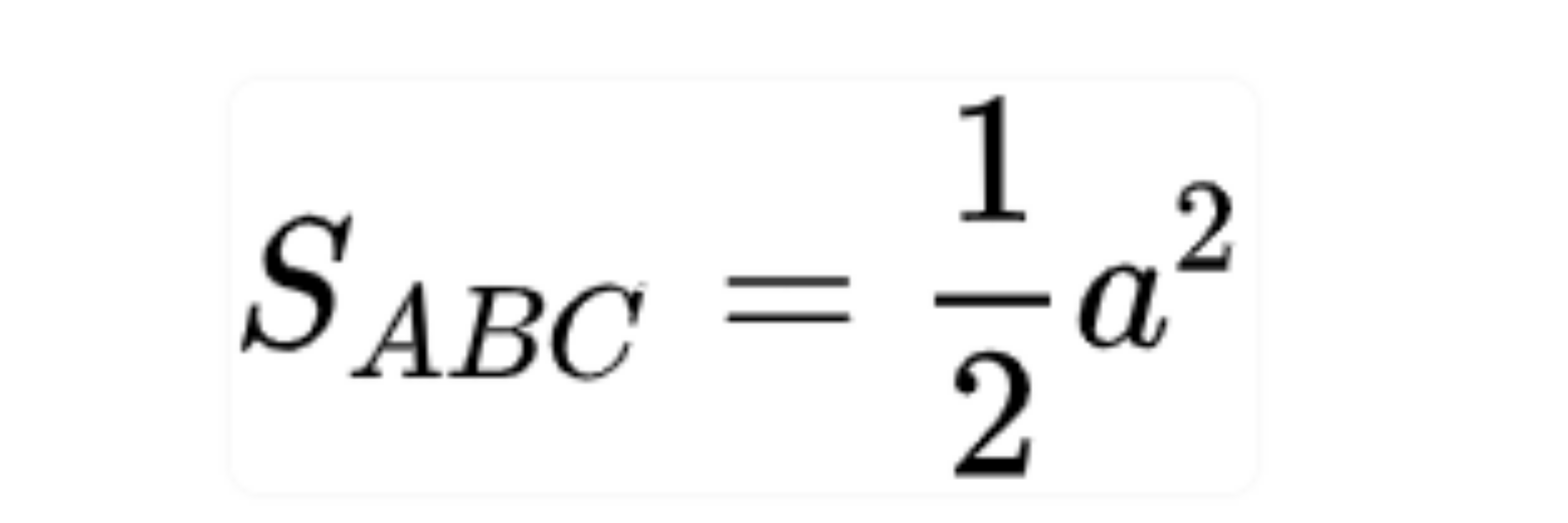
6. Công thức tính diện tích tam giác trong hệ tọa độ Oxyz
Trong không gian Oxyz, diện tích tam giác ABC được tính theo công thức:
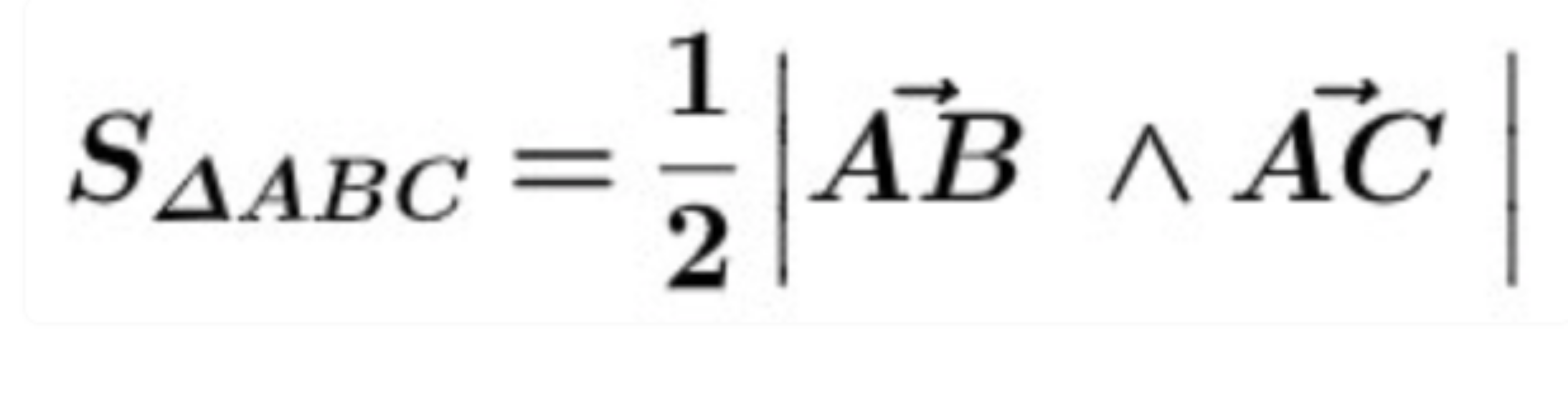
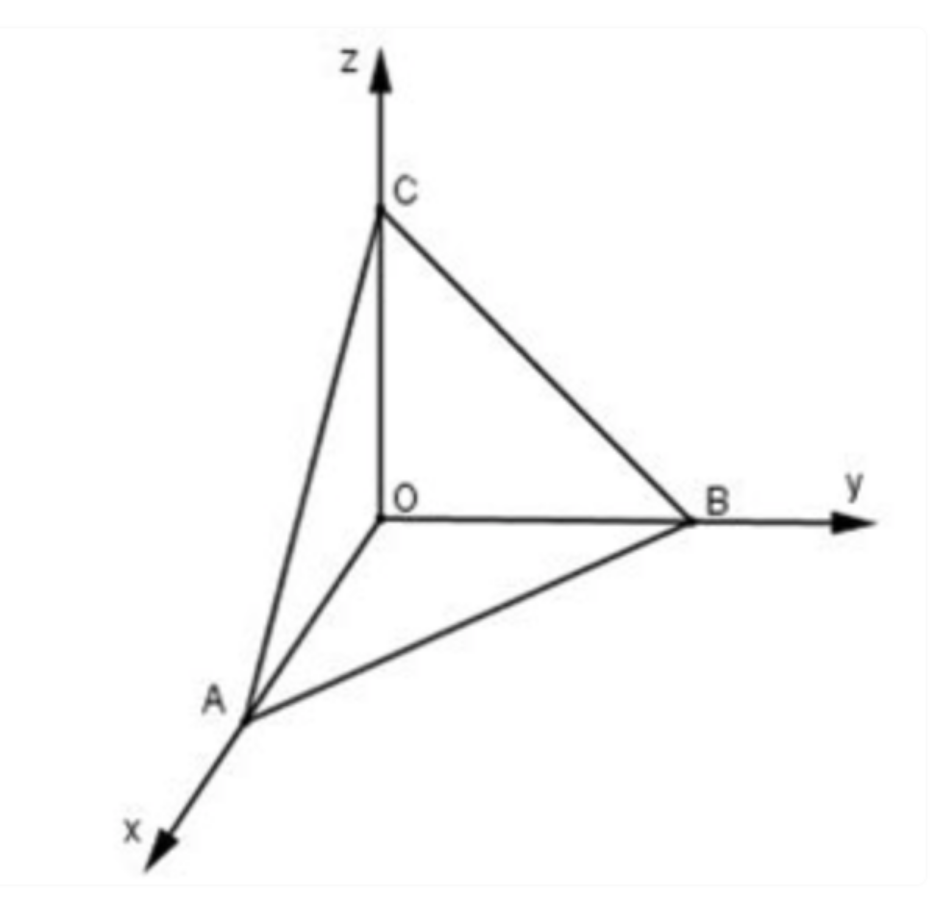
Mở rộng: Nếu ta biết diện tích hình tam giác, ta có thể tính:
- Chiều cao: h = (S x 2) : a
- Cạnh đáy: a = (S x 2) : h
III. Hướng dẫn cách tính diện tích hình Tam giác
1. Sử dụng cạnh đáy và chiều cao
Bước 1: Đầu tiên, tìm đáy và chiều cao của tam giác
Vì đáy của tam giác là 1 cạnh của tam giác nên chiều cao là kích thước từ đáy đến đỉnh cao nhất của tam giác.
Thường thì đề dài sẽ cho bạn dữ kiện chiều cao. Nếu không bạn cũng có thể tìm được bằng cách vẽ 1 đường vuông góc từ đáy đến đỉnh đối diện.
Ví dụ: Cho tam giác có chiều dài cạnh đáy là 5 cm, và chiều cao là 3 cm.
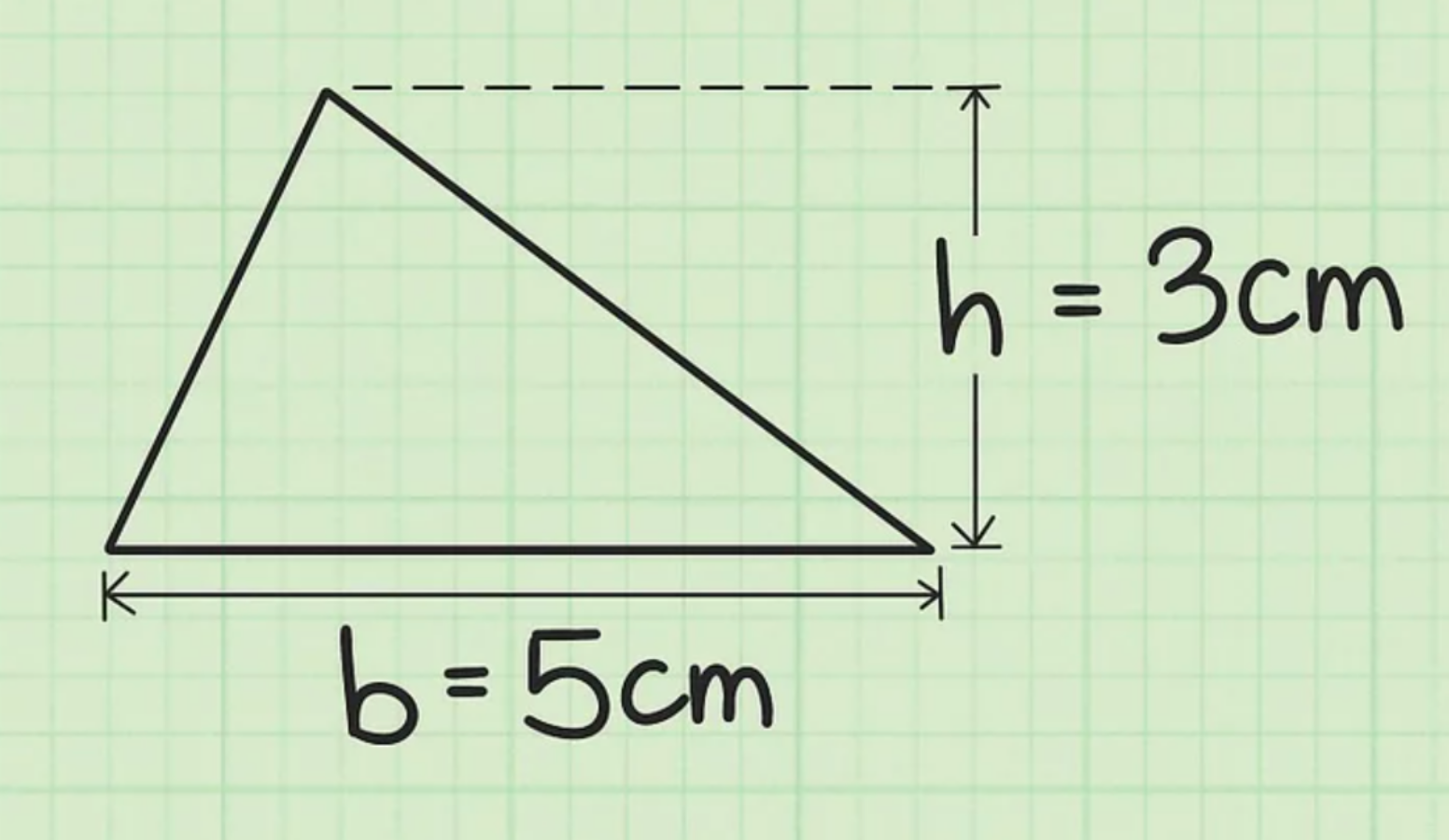
Bước 2: Sau đó, thiết lập công thức tính diện tích tam giác
Công thức là S = ½ (bh)
Trong đó: b là chiều dài của cạnh đáy tam giác, h là chiều cao của tam giác.
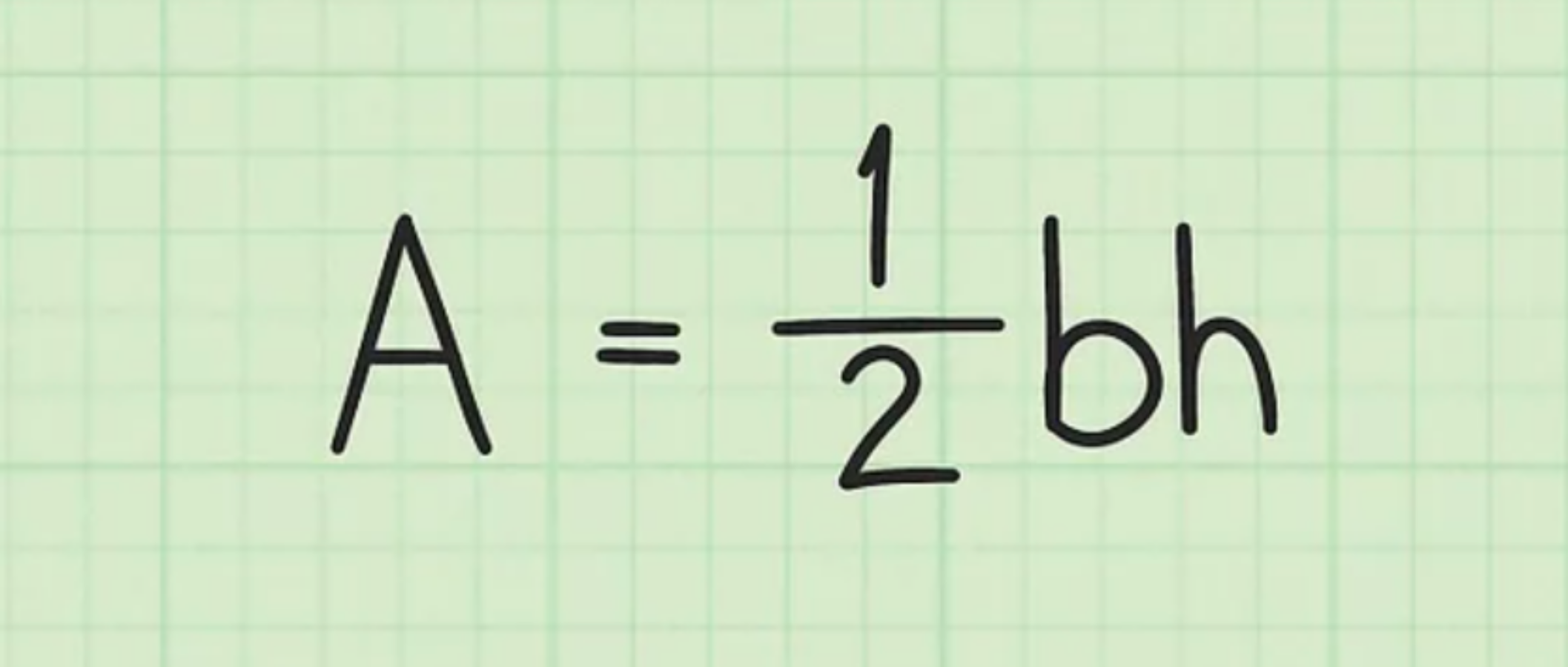
Bước 3: Tiếp theo, thay cạnh đáy và chiều cao vào công thức
Tới đây, bạn nhân 2 giá trị lại với nhau, rồi nhân kết quả cho. ½. Khi đó, bạn sẽ tìm được diện tích tam giác theo đơn vị vuông.
Xét theo ví dụ trên: Chiều dài cạnh đáy là 5 cm và chiều cao là 3 cm, suy ra:
- S = ½ (bh)
- S = ½ (5) (3)
- S = ½ (15)
- S = 7,5
Vậy diện tích hình tam giác sẽ là 7,5 cm vuông.

Bước 4: Cuối cùng, tìm diện tích của tam giác vuông
Theo tính chất, tam giác vuông có 2 cạnh vuông góc với nhau và 1 cạnh góc vuông sẽ là chiều cao của tam giác. Nên bạn có thể sử dụng công thức: S = ½ (bh) để tìm diện tích.
Thông qua định lý Pytago (a2 + b2 = c2), bạn cũng có thể tìm được cạnh còn thiếu nếu đã biết độ dài 1 cạnh.
Ví dụ: Cho cạnh huyền của tam giác là c, chiều cao là a và cạnh đáy là b. Biết cạnh huyền dài 5 cm, cạnh đáy là 4 cm thì bạn có thể sử dụng định lý Pytago để tìm chiều cao như sau:
- a2 + b2 = c2
- a2 + 4 = 52
- a2 + 16 = 25
- a2 + 16 – 16 = 25 – 16
- a2 = 9
- a = 3
Từ đó, bạn có thể thêm 2 cạnh vuông góc (a và b) vào công thức, thay thế cho cạnh đáy và chiều cao như sau:
- S = ½ (bh)
- S = ½ (4) (3)
- S = ½ (12)
- S = 6
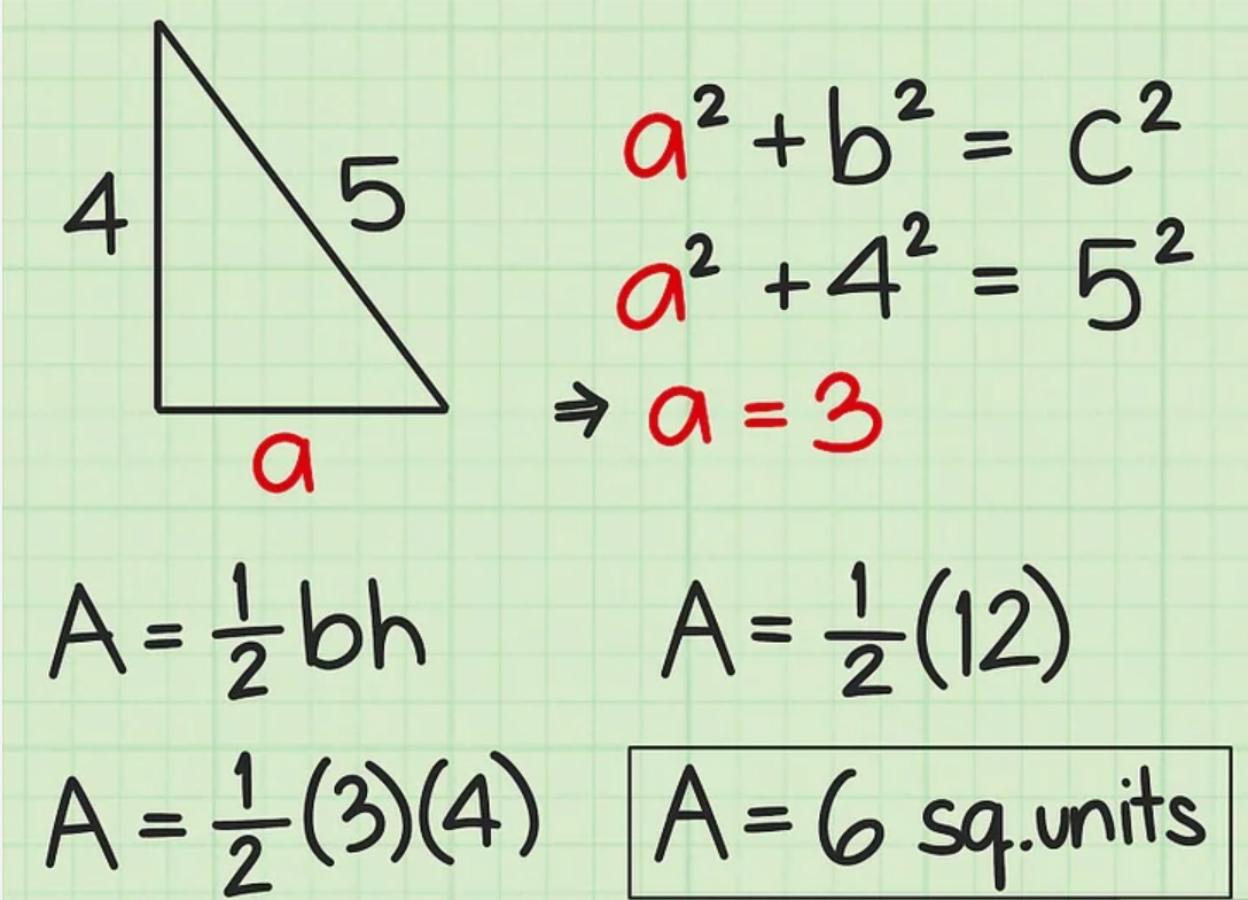
2. Sử dụng chiều dài các cạnh
Bước 1: Trước tiên, tính nửa chu vi tam giác
Đầu tiên, để tính nửa chu vi bạn cần phải tính chu vi tam giác trước bằng cách cộng chiều dài 3 cạnh với nhau. Rồi nhân kết quả với ½
Giả sử: Cho tam giác có chiều dài 3 cạnh lần lượt là 5 cm, 4 cm, và 3 cm, nửa chu vi sẽ là:
S = ½ (3 + 4 + 5)
S = ½ (12) = 6
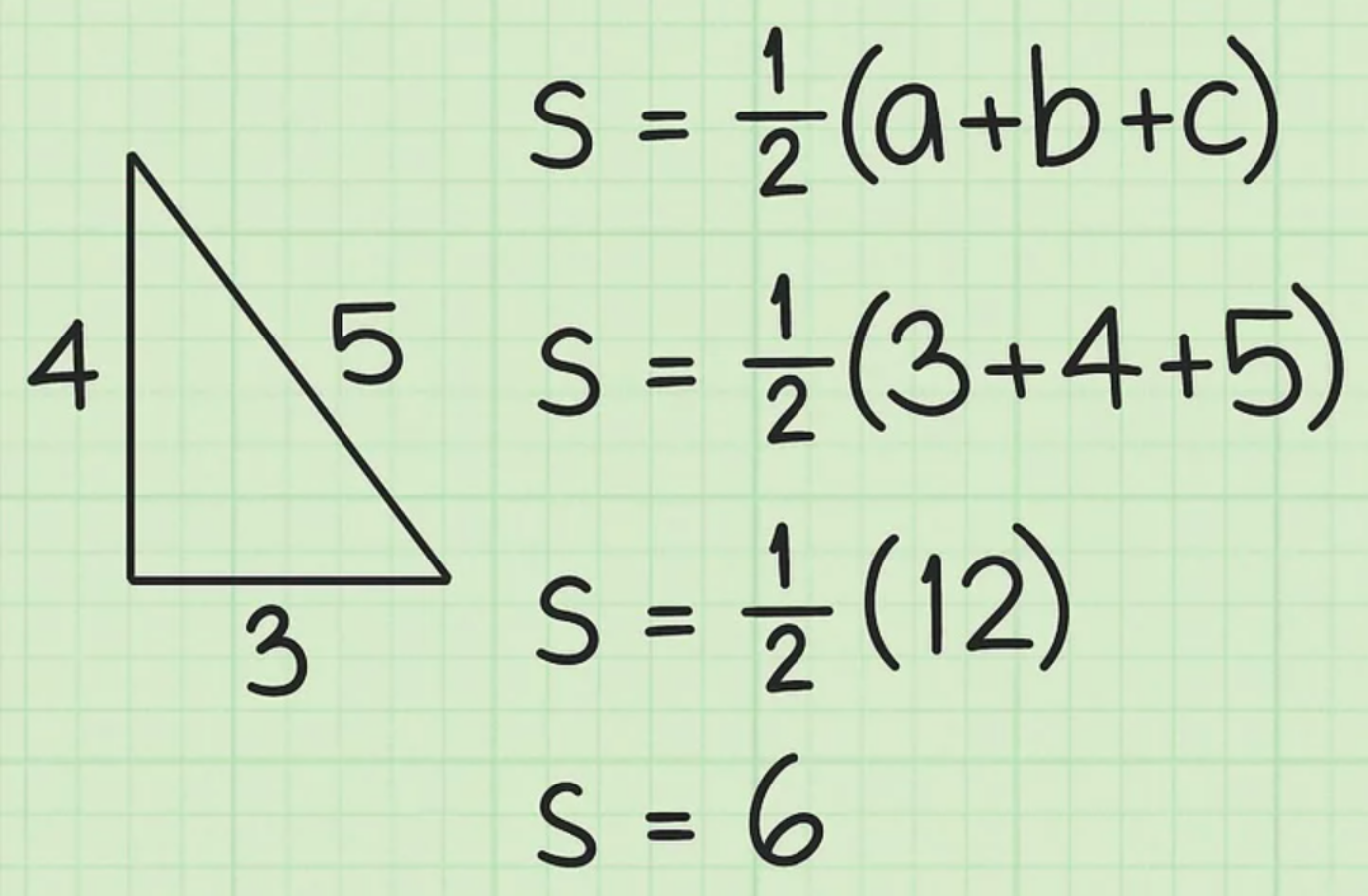
Bước 2: Tiến hành thiết lập công thức Heron
Công thức:
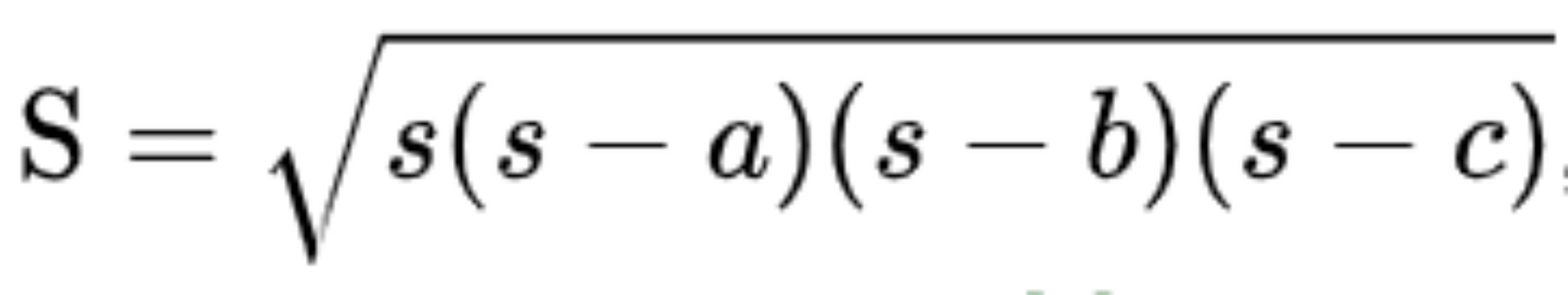
Trong đó: S là nửa chu vi tam giác và a, b, c lần lượt là chiều dài 3 cạnh của tam giác.
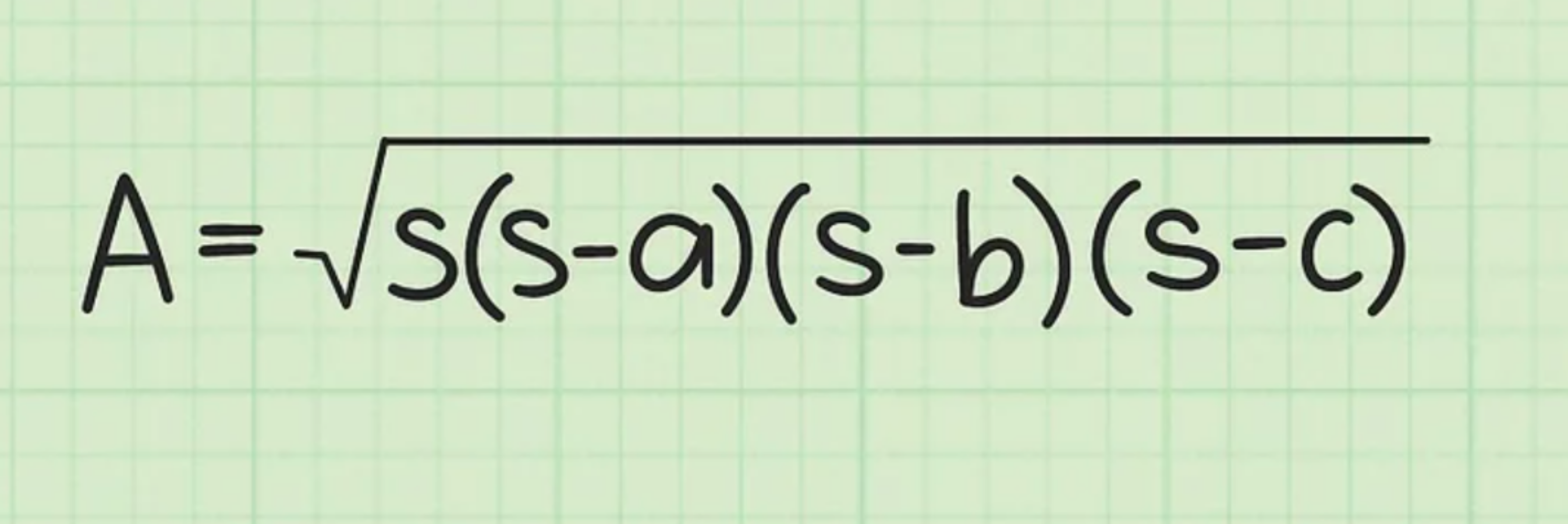
Bước 3: Sau đó, bạn thay nửa chu vi và chiều dài 3 cạnh tam giác vào công thức
Tới đây, bạn tiến hành thay giá trị 3 cạnh vào công thức
Giả sử:
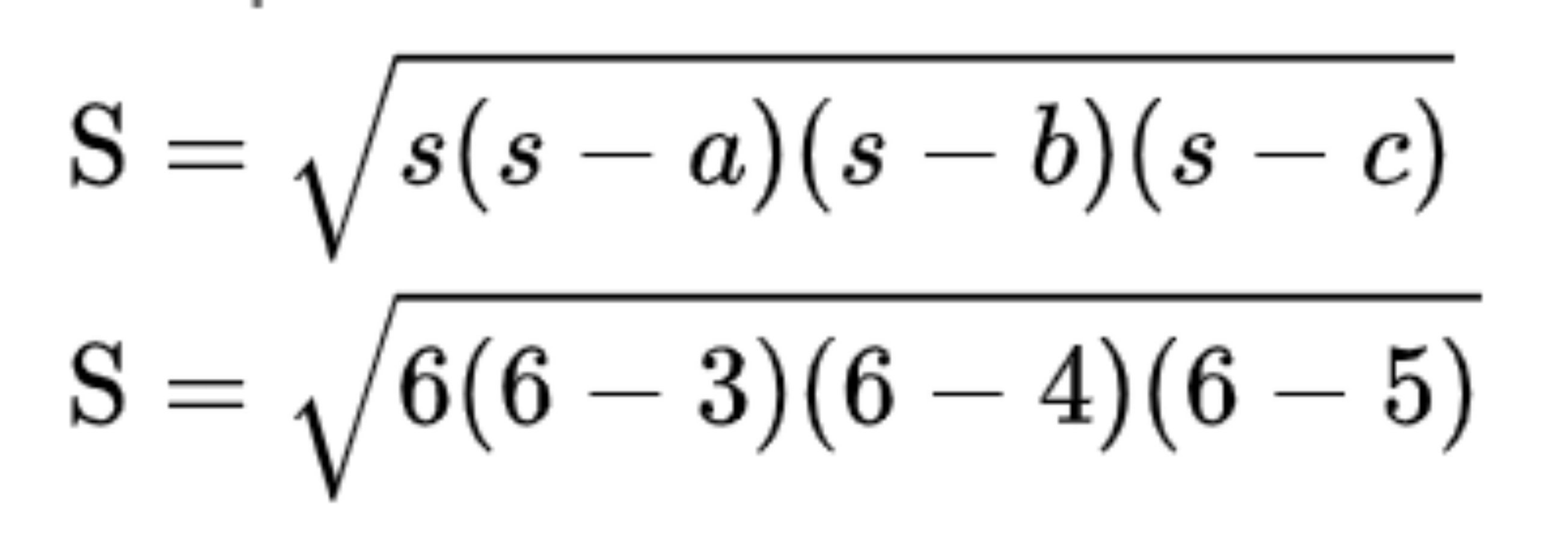
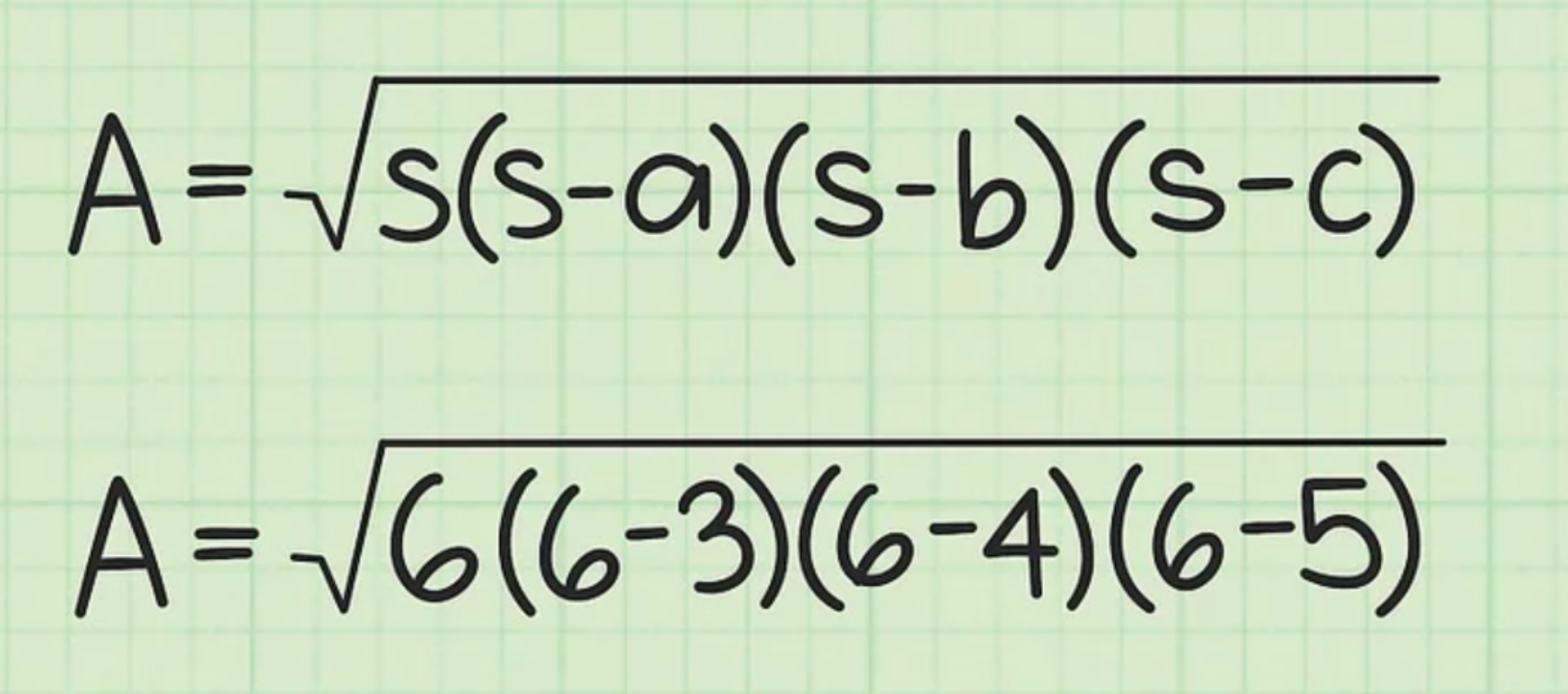
Bước 4: Tiếp theo, tính toán giá trị trong dấu ngoặc đơn
Bạn tiếp tục lấy nửa chu vi trừ đi chiều dài của từng cạnh rồi nhân 3 giá trị này với nhau.
Giả sử:
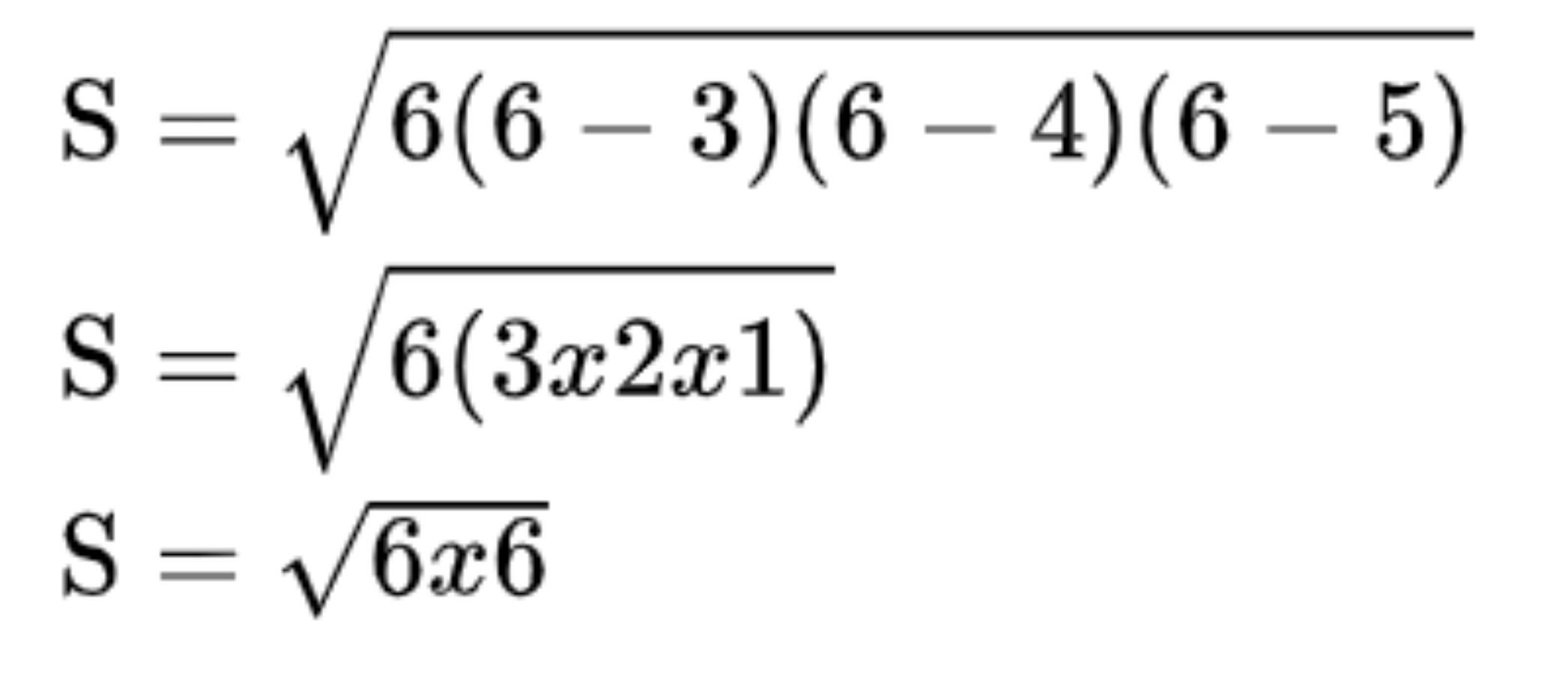
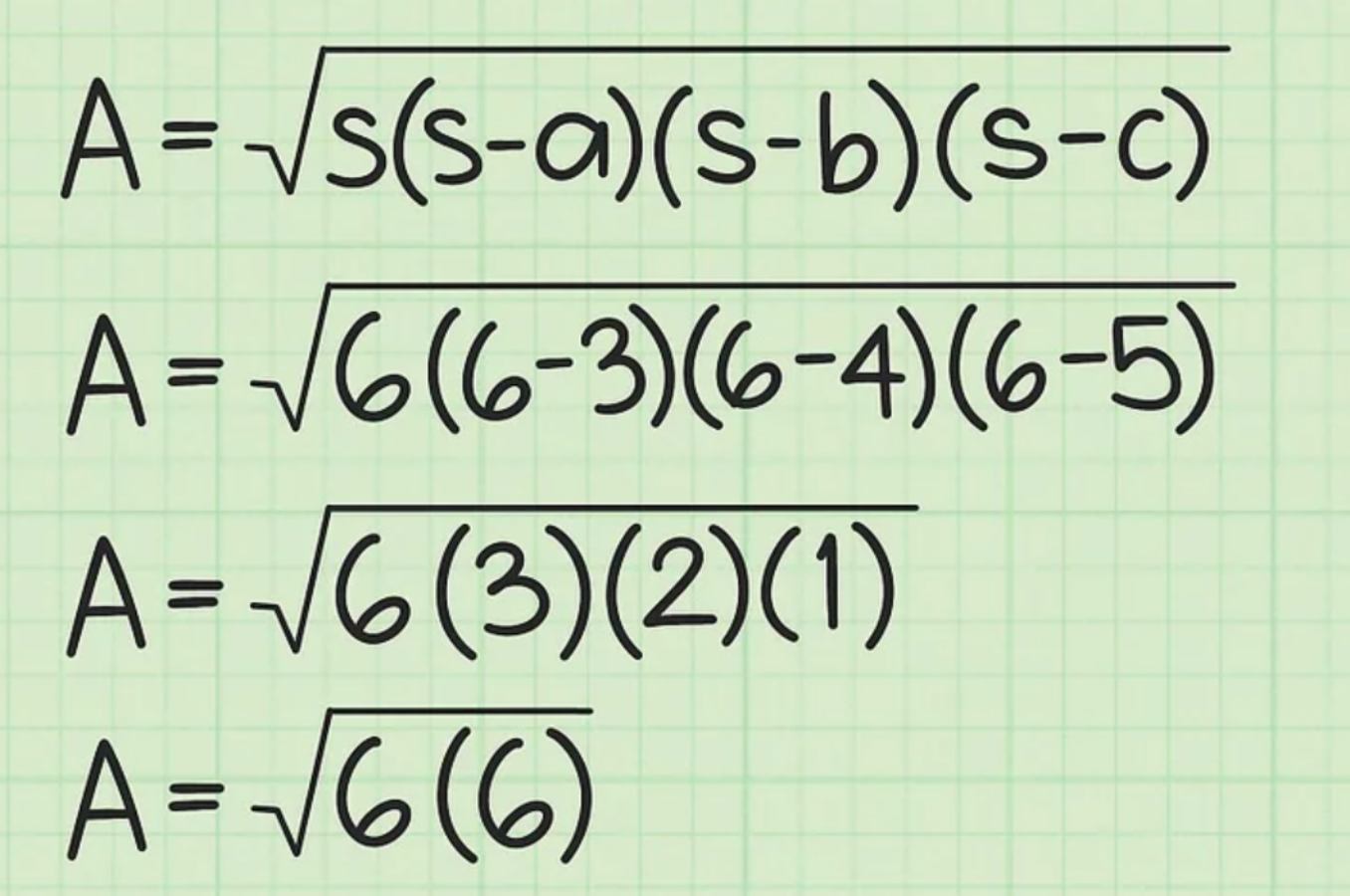
Bước 5: Cuối cùng, bạn nhân 2 giá trị bên dưới dấu căn với nhau
Bạn sẽ tìm được kết quả diện tích tam giác sau khi căn bậc hai của chúng. Nhớ ghi đáp số theo đơn vị vuông.
Giả sử:
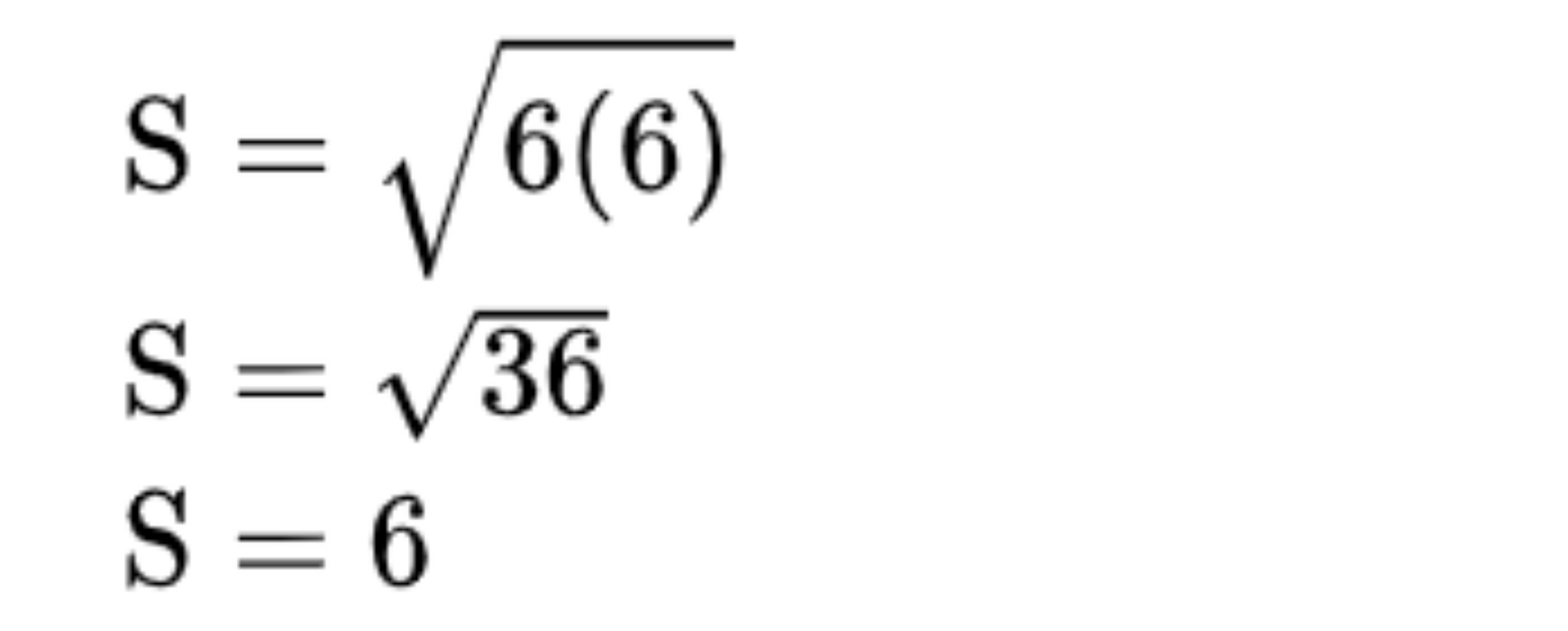

3. Sử dụng một cạnh của tam giác đều
Bước 1: Trước tiên, tìm chiều dài 1 cạnh của tam giác
Theo tính chất, tam giác đều là tam giác có 3 cạnh và 3 góc bằng nhau. Do đó, biết được chiều dài 1 cạnh sẽ cho bạn biết chiều dài của cả 3 cạnh
Giả sử: Cho 1 tam giác có 3 cạnh dài 6 cm.
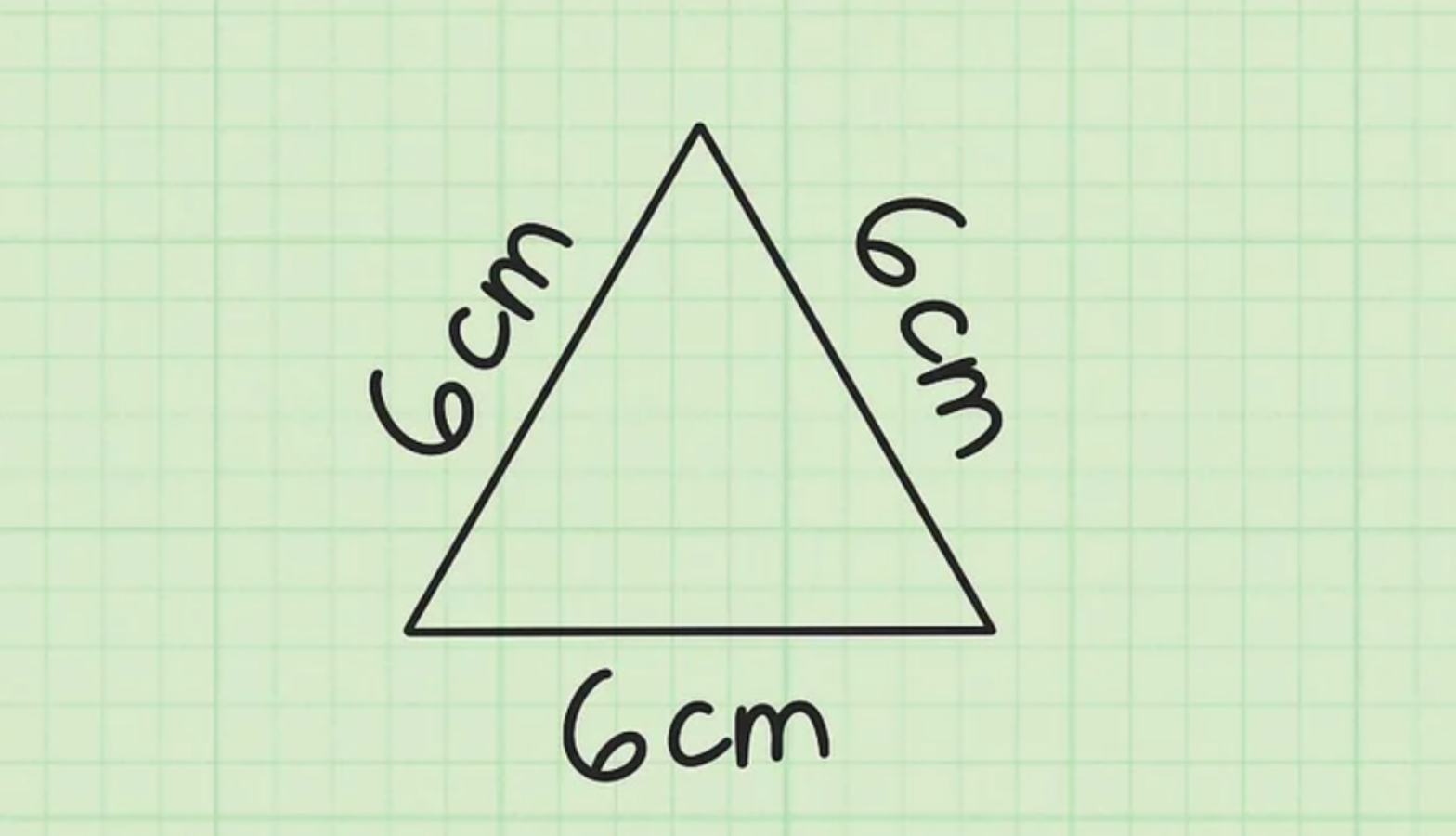
Bước 2: Sau đó, bạn thiết lập công thức tính diện tích tam giác đều
Công thức:
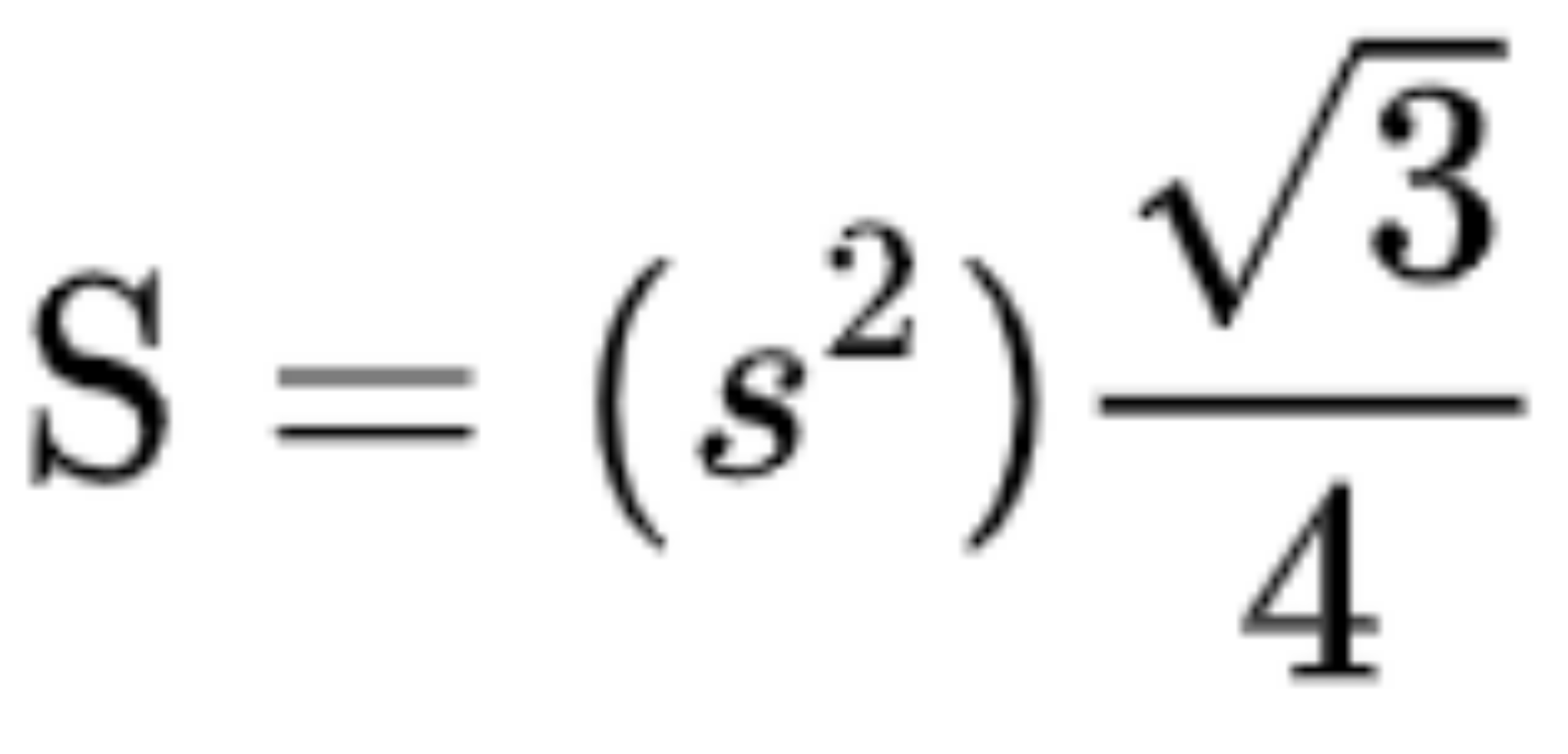
Trong đó S là chiều dài 1 cạnh của tam giác đều.
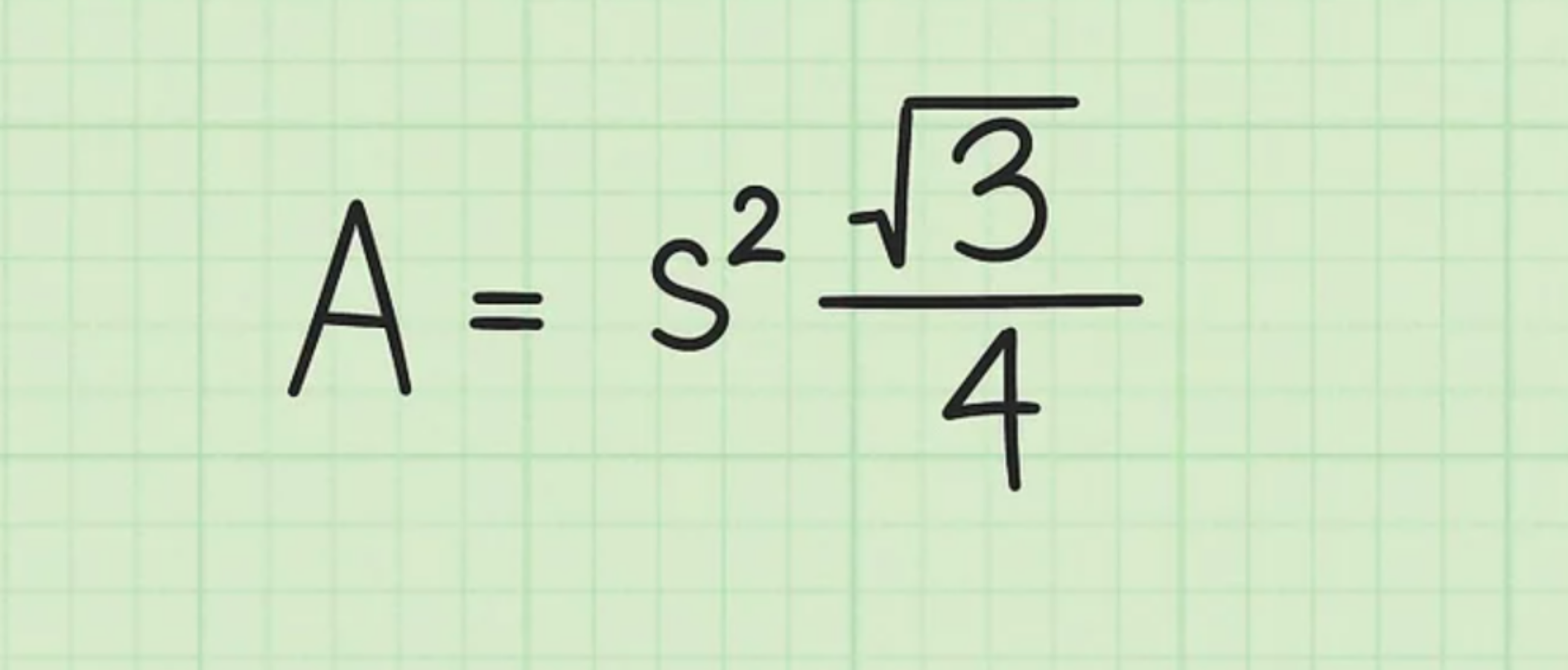
Bước 3: Tiếp theo, bạn thay chiều dài cạnh tam giác vào công thức
Tới đây, bạn thay số liệu vào công thức.
Xét theo ví dụ trên: Cho tam giác đều có cạnh dài 6 cm, suy ra:
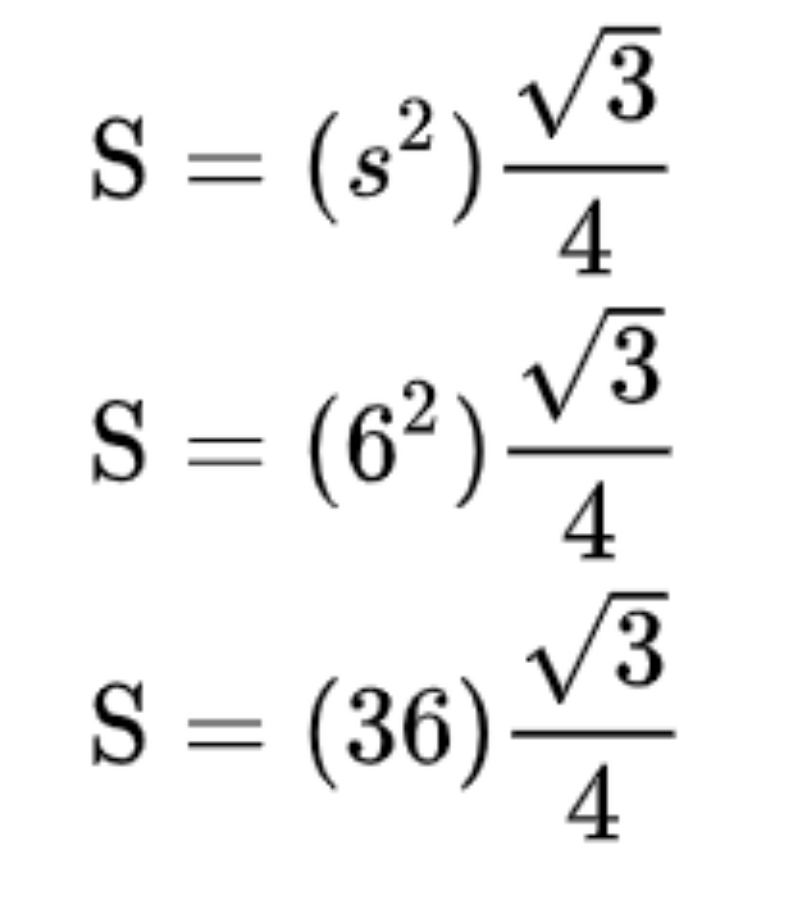
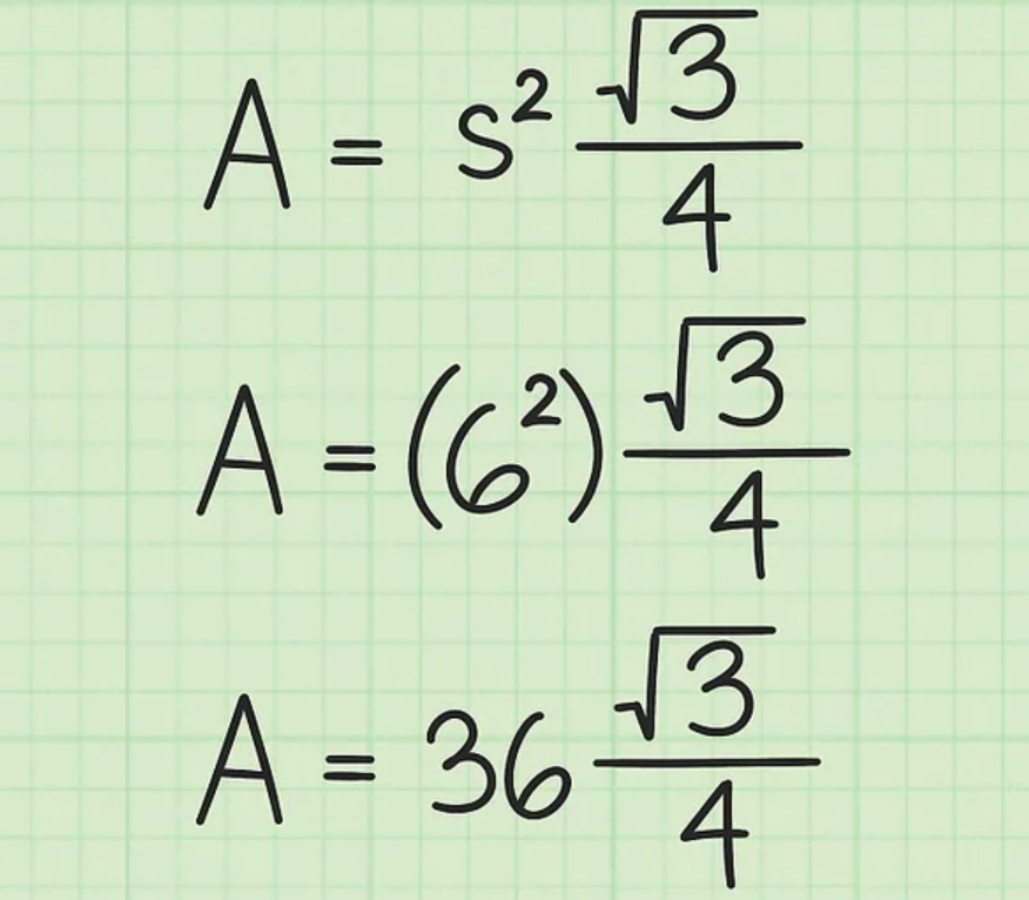
Bước 4: Nhân giá trị bình phương cho căn 3
Bạn nên sử dụng máy tính để tính giá trị hoặc sử dụng kết quả đã được làm tròn là 1,732.
Giả sử:
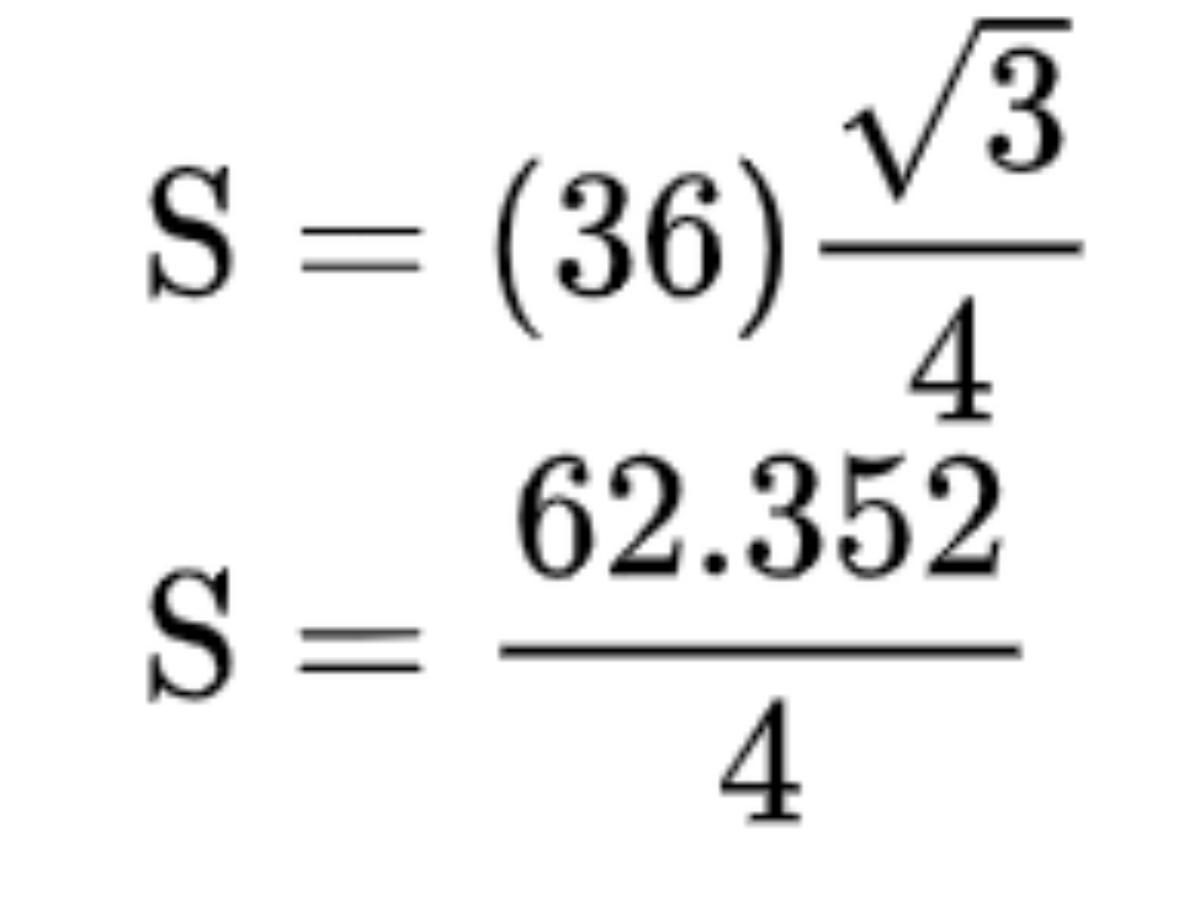
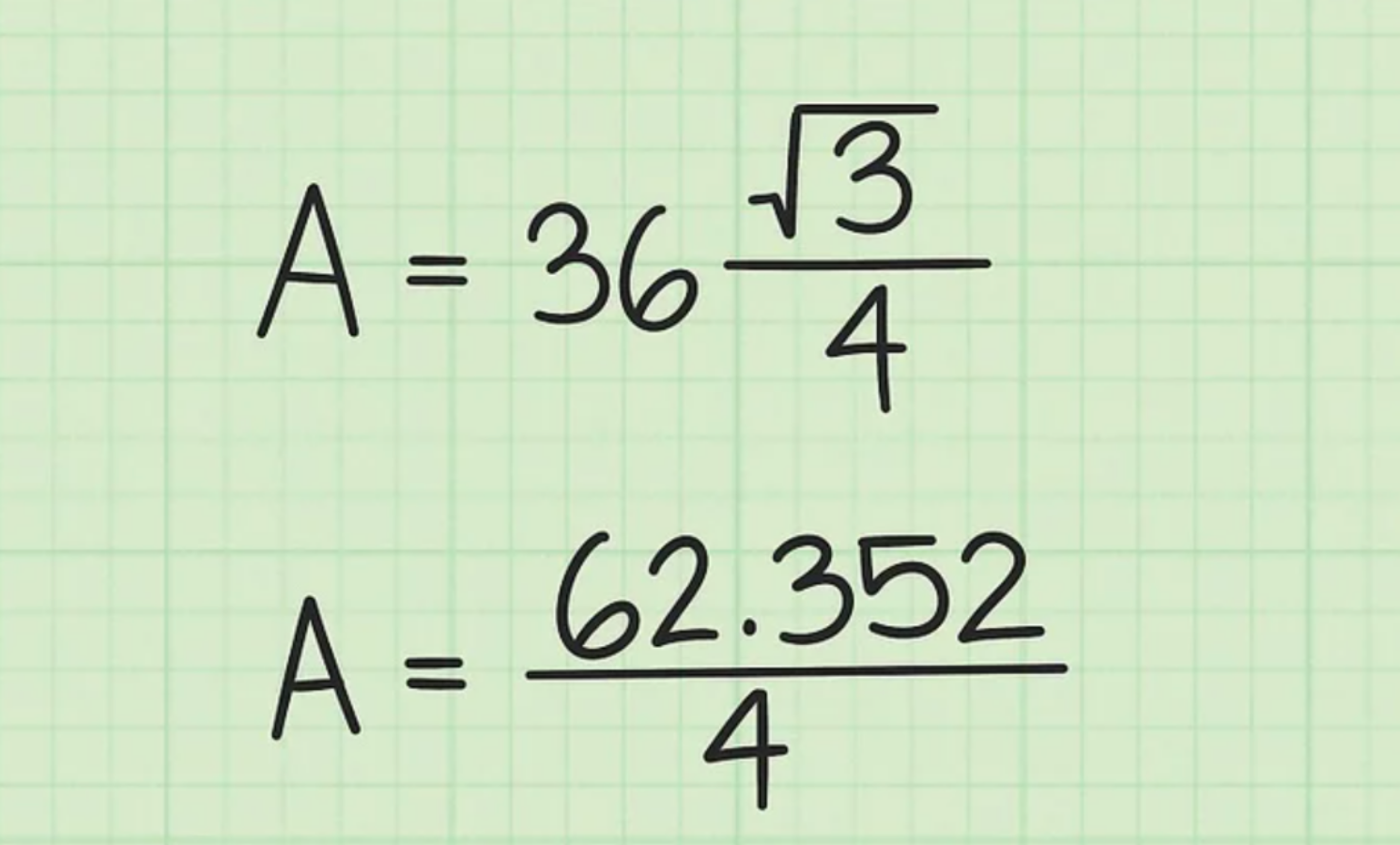
Bước 5: Cuối cùng, chia kết quả cho 4
Tới đây, bạn sẽ tìm được diện tích tam giác theo đơn vị vuông khi chia kết quả cho 4.
Giả sử:
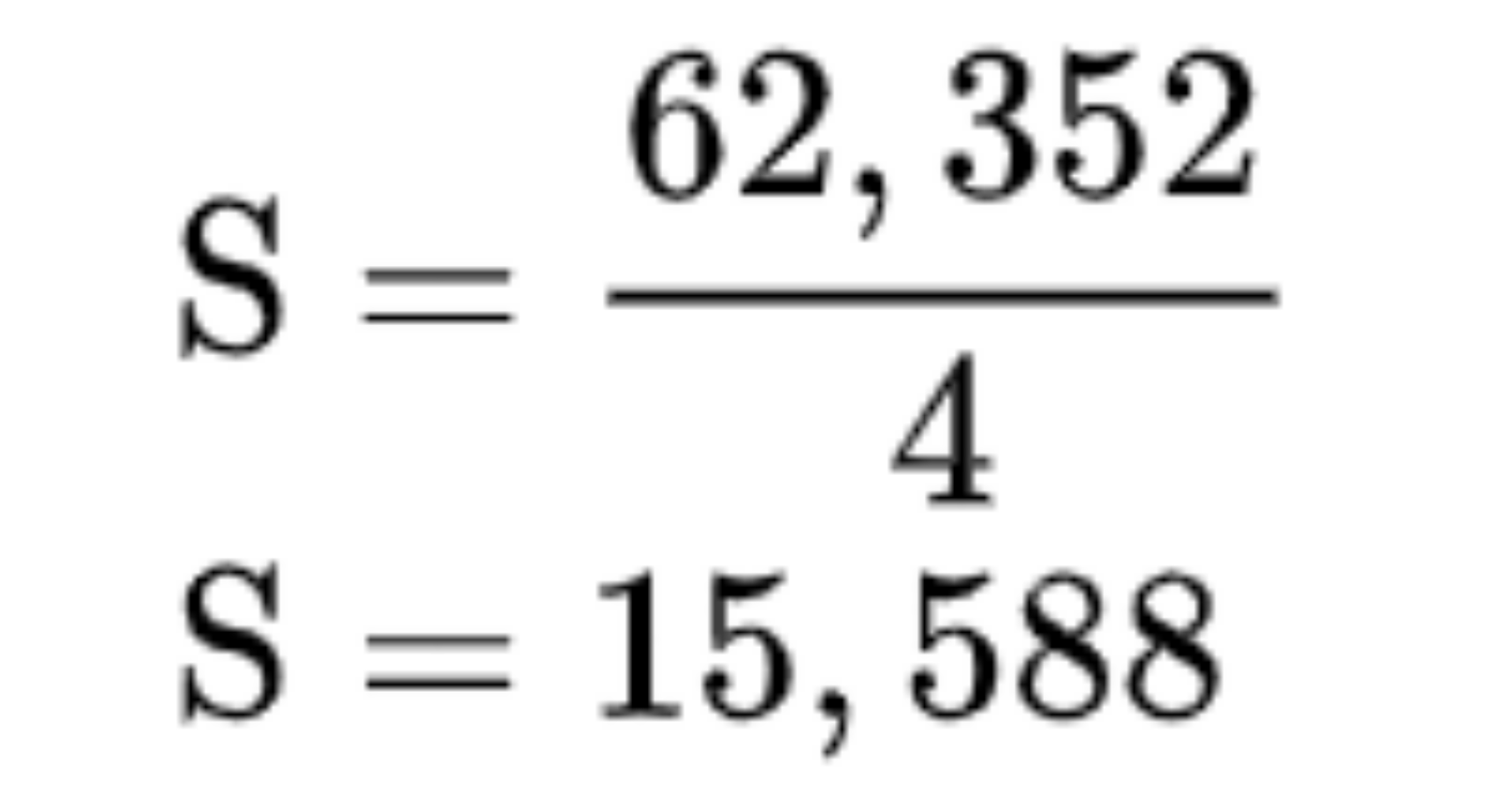
Vậy diện tích của tam giác đều với cạnh dài 6 cm là khoảng 15,59 cm2.

4. Sử dụng hàm lượng giác
Bước 1: Đầu tiên, bạn tìm chiều dài 2 cạnh kề nhau trong tam giác và góc được tạo bởi 2 cạnh đó
Vì 2 cạnh kề của tam giác là 2 cạnh giao nhau ở đỉnh tam giác nên góc được tạo bởi 2 cạnh đó là góc nằm giữa chúng.
Giả sử: Cho tam giác có 2 cạnh kề nhau với chiều dài lần lượt là 150 cm và 231 cm. Góc tạo bởi chúng là 123°.
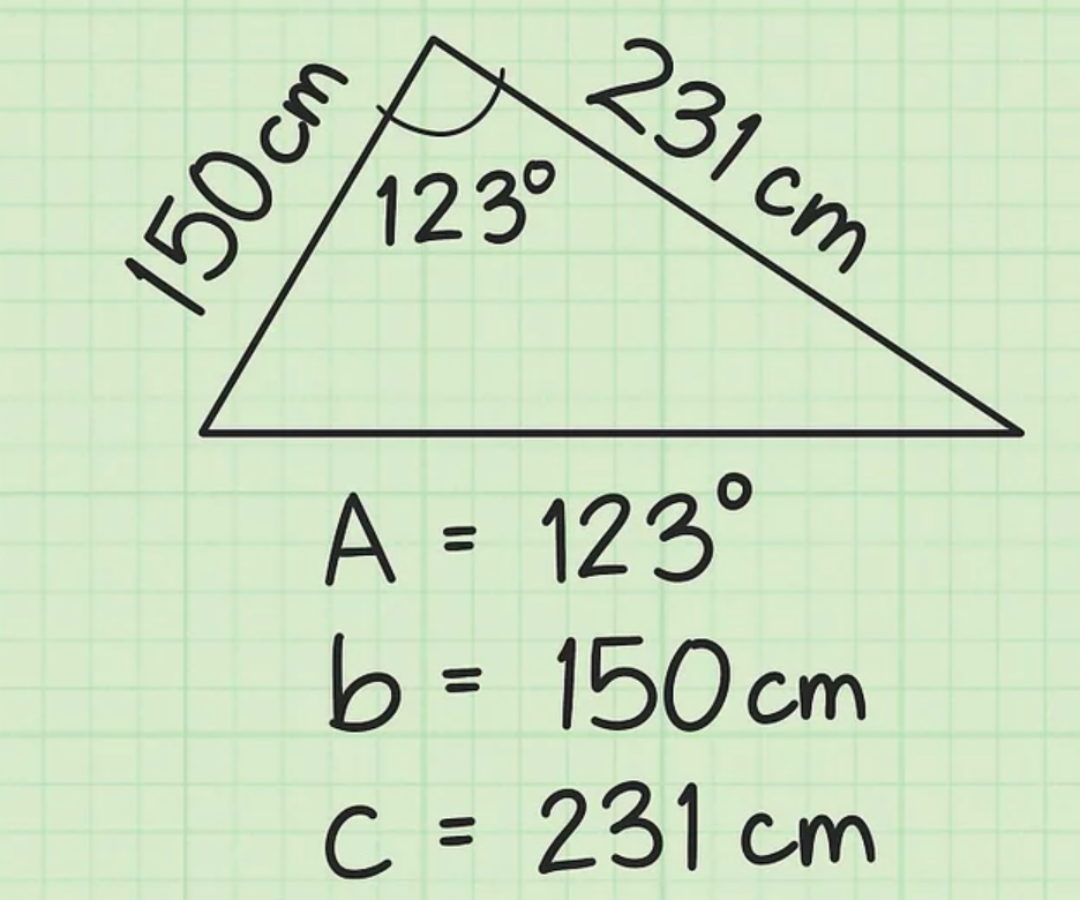
Bước 2: Sau đó, bạn thiết lập công thức hàm lượng giác để tính diện tích tam giác
Công thức:
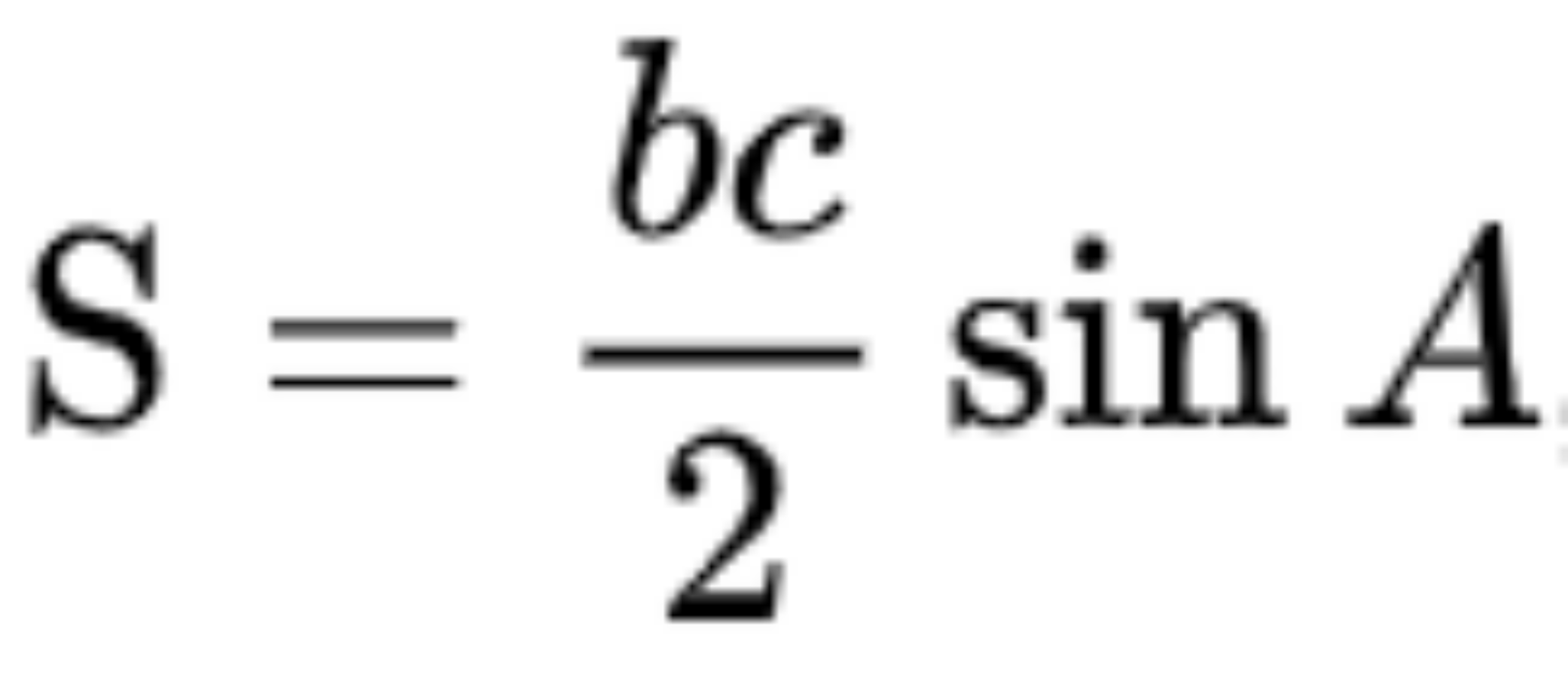
Trong đó b, c là 2 cạnh kề của tam giác và A là góc nằm giữa 2 cạnh đó.
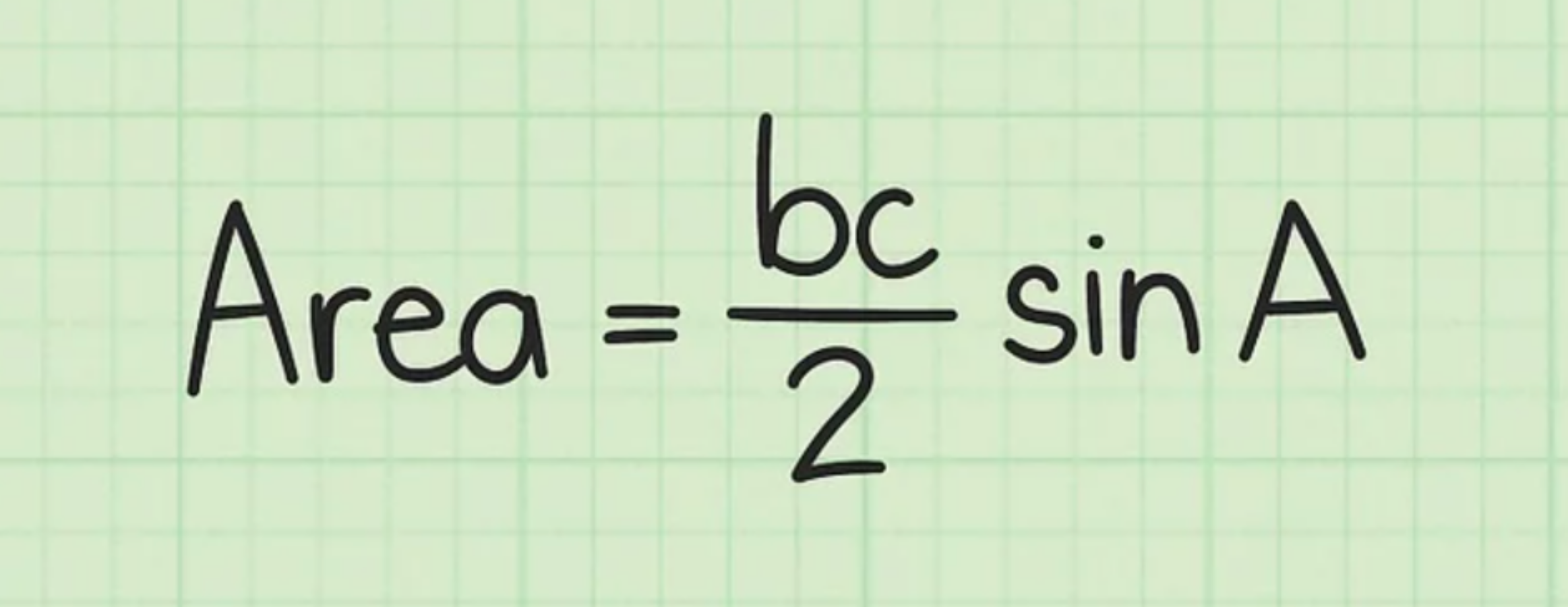
Bước 3: Tiếp theo, thay chiều dài các cạnh vào công thức
Bạn tiến hành thay các giá trị b, c rồi nhân chúng lại với nhau, sau đó chia cho 2.
Giả sử:
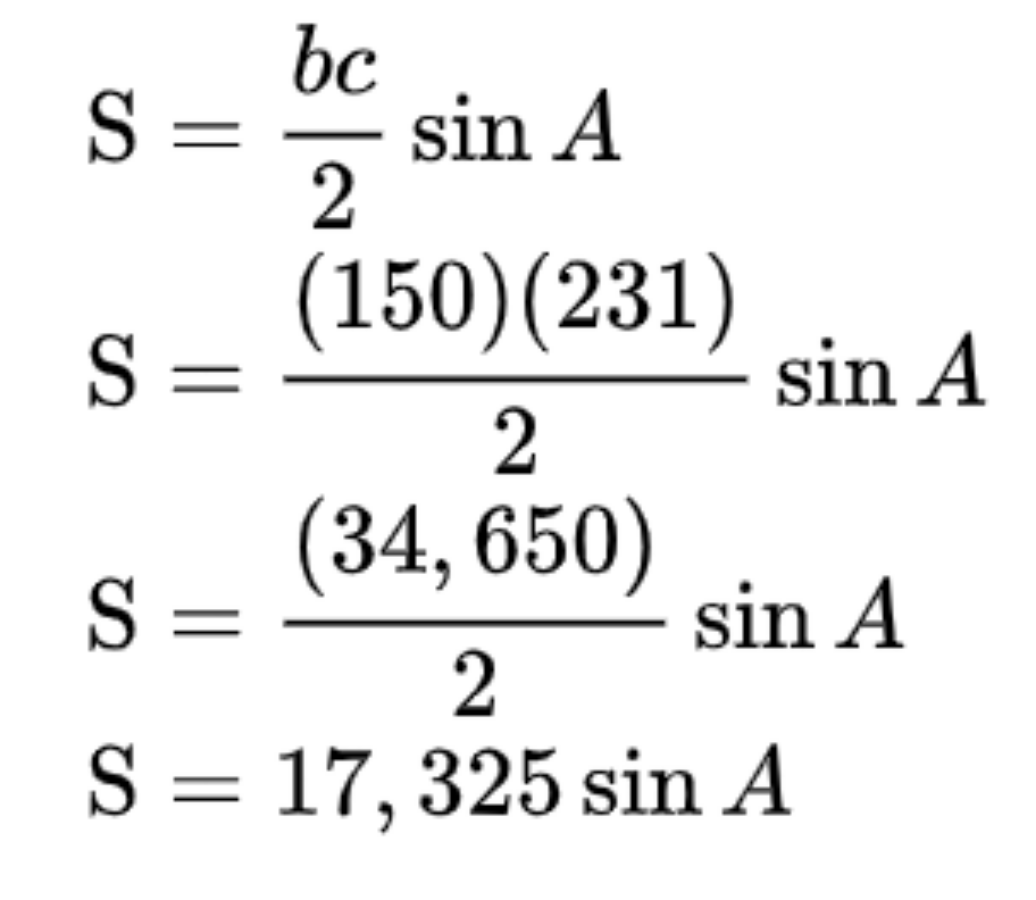

Bước 4: Kế đó, bạn thay giá trị sin của góc vào công thức
Tới đây, bạn có thể dùng máy tính để tìm sin bằng cách nhập vào giá trị của góc và sau đó bấm nút “SIN”.
Giả sử: Sin của góc 123° là 0,83867, suy ra công thức:
S = 17,325 sin A
S = 17,325 x 0,83867

Bước 5: Cuối cùng, bạn nhân 2 giá trị với nhau
Khi tìm được diện tích tam giác, nhớ viết đơn vị vuông là xong.

IV. Một số bài tập tính diện tích hình tam giác
1. Bài tập tính diện tích hình tam giác có lời giải
Câu 1: Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 24dm.
Giải: Chiều cao 24dm = 2,4m
Diện tích tam giác là:
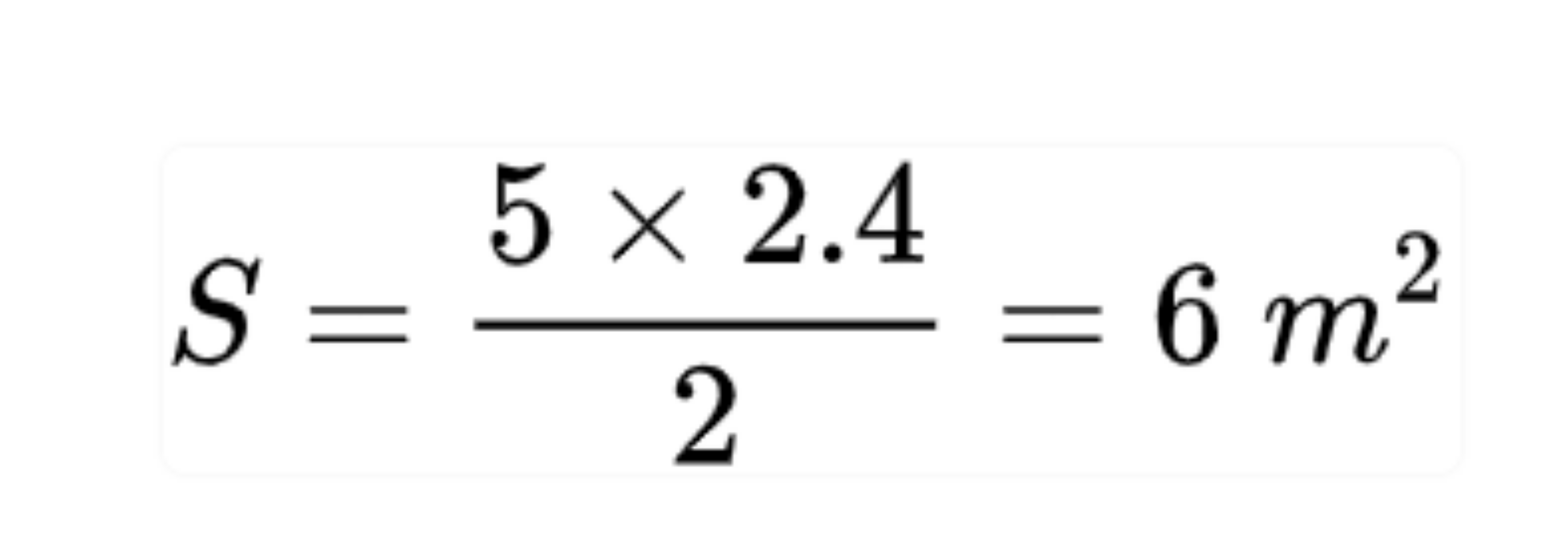
Câu 2: Tam giác ABC có cạnh BC = 7, cạnh AB = 5, góc B bằng 60 độ. Tính diện tích tam giác ABC?
Giải:
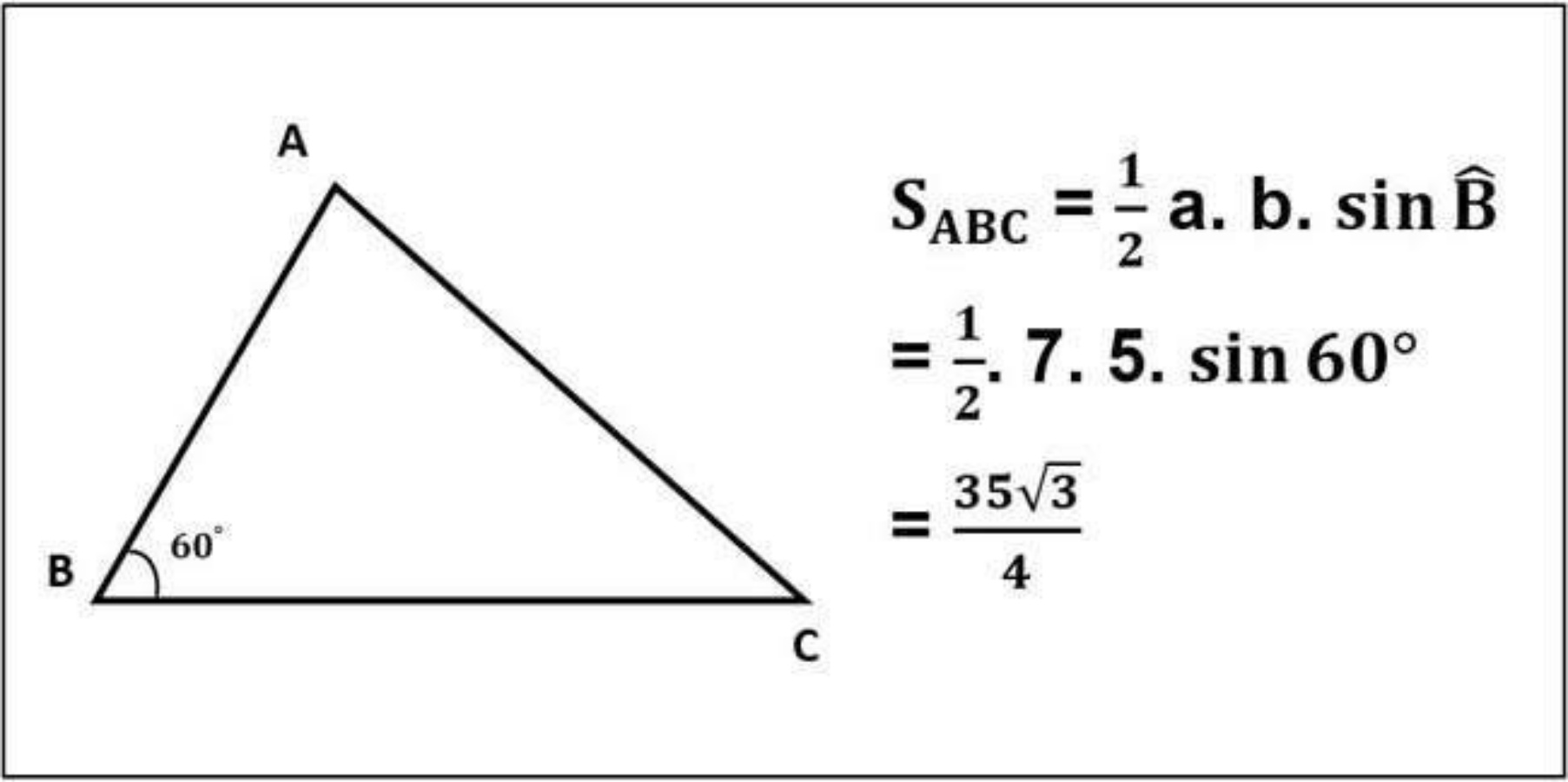
Câu 3: Tính diện tích hình tam giác có độ dài cạnh AB = 8, AC = 7, CB = 9
Giải:
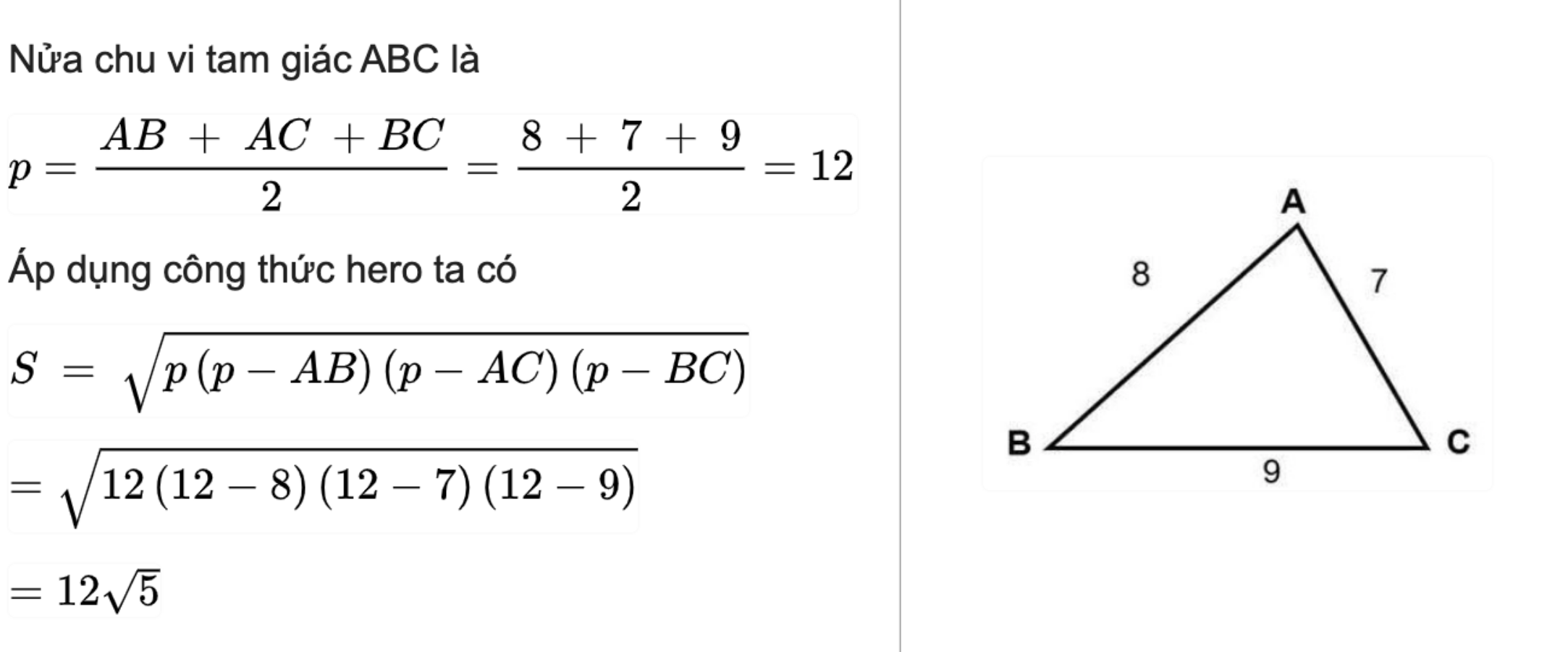
Câu 4: Cho tam giác ABC, độ dài các cạnh a = 6, b = 7, c = 5, R = 3 (R là bán kính đường tròn ngoại tiếp tam giác ABC). Tính diện tích của tam giác ABC.
Giải:
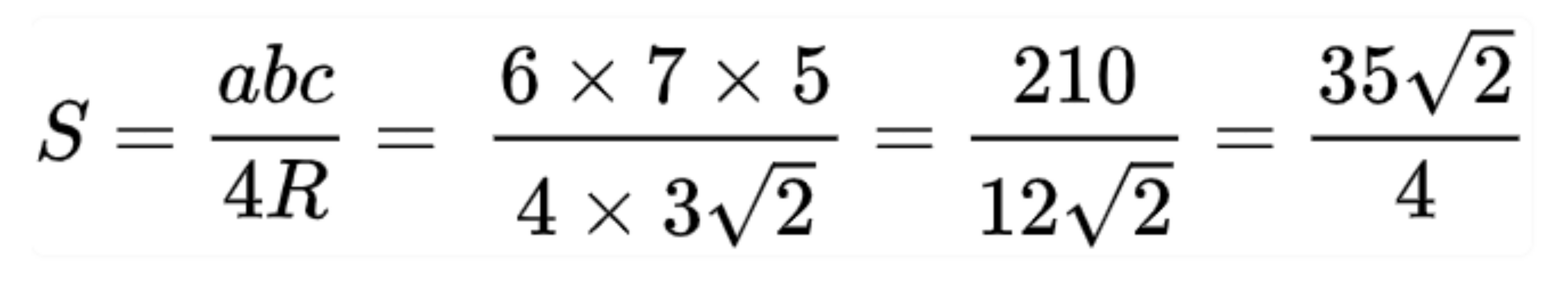
Câu 5: Tính diện tích tam giác ABC biết độ dài các cạnh AB = 20, AC = 21, BC = 15, r = 5 (r là bán kính đường tròn nội tiếp tam giác ABC).
Giải:
Nửa chu vi tam giác là:
![]()
r= 5
Diện tích tam giác là:
S = p x r = 28 x 5 = 140
Câu 6: Tính diện tích của tam giác vuông có:
a) Hai cạnh góc vuông lần lượt là 3cm và 4cm
b) Hai cạnh góc vuông lần lượt là 6m và 8m
Giải:
a) Diện tích của hình tam giác là: (3 x 4) : 2 = 6 (cm2). Đáp số: 6cm2
b) Diện tích của hình tam giác là: (6 x 8) : 2 = 24 (m2). Đáp số: 24m2
Câu 7: Tính diện tích của tam giác cân có:
a) Độ dài cạnh đáy bằng 6cm và đường cao bằng 7cm
b) Độ dài cạnh đáy bằng 5m và đường cao bằng 3,2m
Giải:
a) Diện tích của hình tam giác là: (6 x 7) : 2 = 21 (cm2). Đáp số: 21cm2
b) Diện tích của hình tam giác là: (5 x 3,2) : 2 = 8 (m2). Đáp số: 8m2
Câu 8: Tính diện tích của tam giác đều có:
a) Độ dài một cạnh tam giác bằng 6cm và đường cao bằng 10cm
b) Độ dài một cạnh tam giác bằng 4cm và đường cao bằng 5cm
Giải:
a) Diện tích hình tam giác là: (6 x 10) : 2 = 30 (cm2). Đáp số: 30cm2
b) Diện tích hình tam giác là: (4 x 5) : 2 = 10 (cm2). Đáp số: 10cm2
Câu 9: Tính diện tích tam giác ABC có độ dài cạnh đáy là 15 cm, chiều cao là 12 cm.
Giải: Diện tích của hình tam giác ABC là: (15 x 12) : 2 = 90 (cm2)
Đáp số: 90 cm2
Câu 10: Trong không gian Oxyz, cho tam giác ABC có tọa độ ba đỉnh lần lượt là A(-1;1;2), B(1;2;3), C(3;-2;0). Tính diện tích tam giác ABC.
Giải:
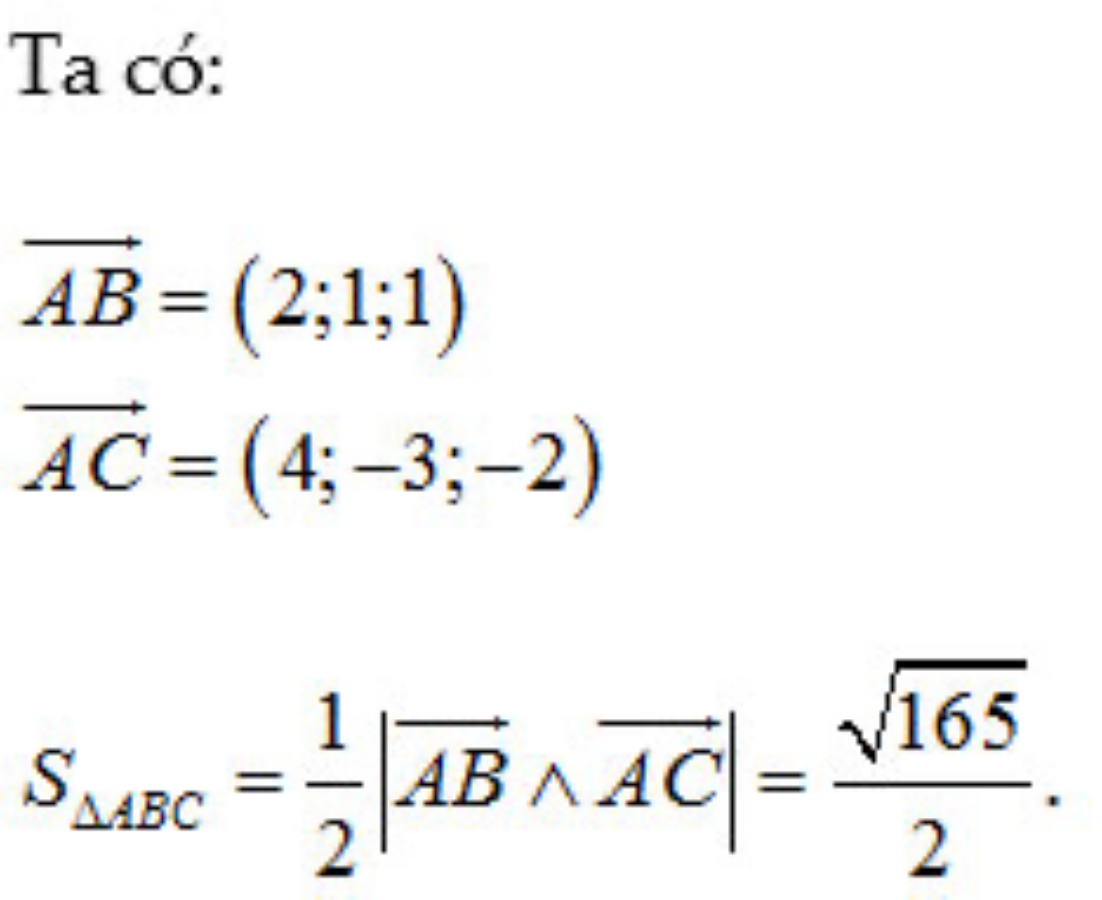
2. Bài tập tính diện tích hình tam giác không có lời giải
Câu 1: Cho hình tam giác MNP có hai cạnh góc vuông lần lượt là 6m và 8m. Tính diện tích của tam giác MNP?
Câu 2: Cho hình tam giác BCD, biết độ dài đáy là ¾ m và chiều cao là ½ m. Tính diện tích của tam giác BCD?
Câu 3: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.
Câu 4: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm
Câu 5: Tính chiều cao AH của hình tam giác ABC vuông tại A. Biết : AB = 60 cm ; AC = 80 cm ; BC = 100 cm.
Câu 6: Một miếng đát hình tam giác có diện tích 288m2, một cạnh đáy bằng 32m. Hổi để diện tích miếng đát tăng thêm 72m2 thì phải tăng cạnh đáy đã cho thêm bao nhiêu mét?
Câu 7: Một hình tam giác có đáy dài 16cm, chiều cao bằng 3/4 độ dài đáy. Tính diện tích hình tam giác đó
Câu 8: Cho hình tam giác vuông ABC (góc A là góc vuông). Biết độ dài cạnh AC là 12dm, độ dài cạnh AB là 90cm. Hãy tính diện tích hình tam giác ABC?
Câu 9: Một quán ăn lạ có hình dạng là 1 tam giác có tổng cạnh đáy và chiều cao là 24m, cạnh đáy bằng 1515 chiều cao. Tính diện tích quán ăn đó?
Câu 10: Một hình tam giác có cạnh đáy bằng 2/3 chiều cao. Nếu kéo dài cạnh đáy thêm 30dm thì diện tích của hình tam giác tăng thêm 27m2. Tính diện tích hình tam giác đó?
Trên đây là công thức Diện tích hình Tam Giác & cách tính diện tích hình Tam Giác đơn giản 2023, nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể tính được diện tích hình Tam Giác một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn thành công.
Tags:
tính diện tích tam giác vuôngtính diện tích tam giác biết 3 cạnhtính diện tích tam giác vuôngcâncông thức tính diện tích tam giác lớp 5

