Các em cần ôn tập kiến thức môn toán để chuẩn bị cho bài kiểm tra sắp tới. Nhưng bạn vẫn chưa biết hình trụ là gì và cách tính thể tích của nó như thế nào?
Đừng lo lắng, đội ĐẢO NGƯỢC Chúng tôi sẽ hướng dẫn các bạn cách tính thể tích khối trụ cực kỳ đơn giản, chi tiết và dễ hiểu qua bài viết dưới đây.
Mục lục bài viết [Ẩn]
I. Xilanh, mặt trụ và mặt trụ là gì?
1. Định nghĩa mặt trụ
mặt trụ là mặt tròn xoay sinh bởi đường thẳng tôi khi quay quanh một đường thẳng Δ song song và cách Δ một khoảng r.
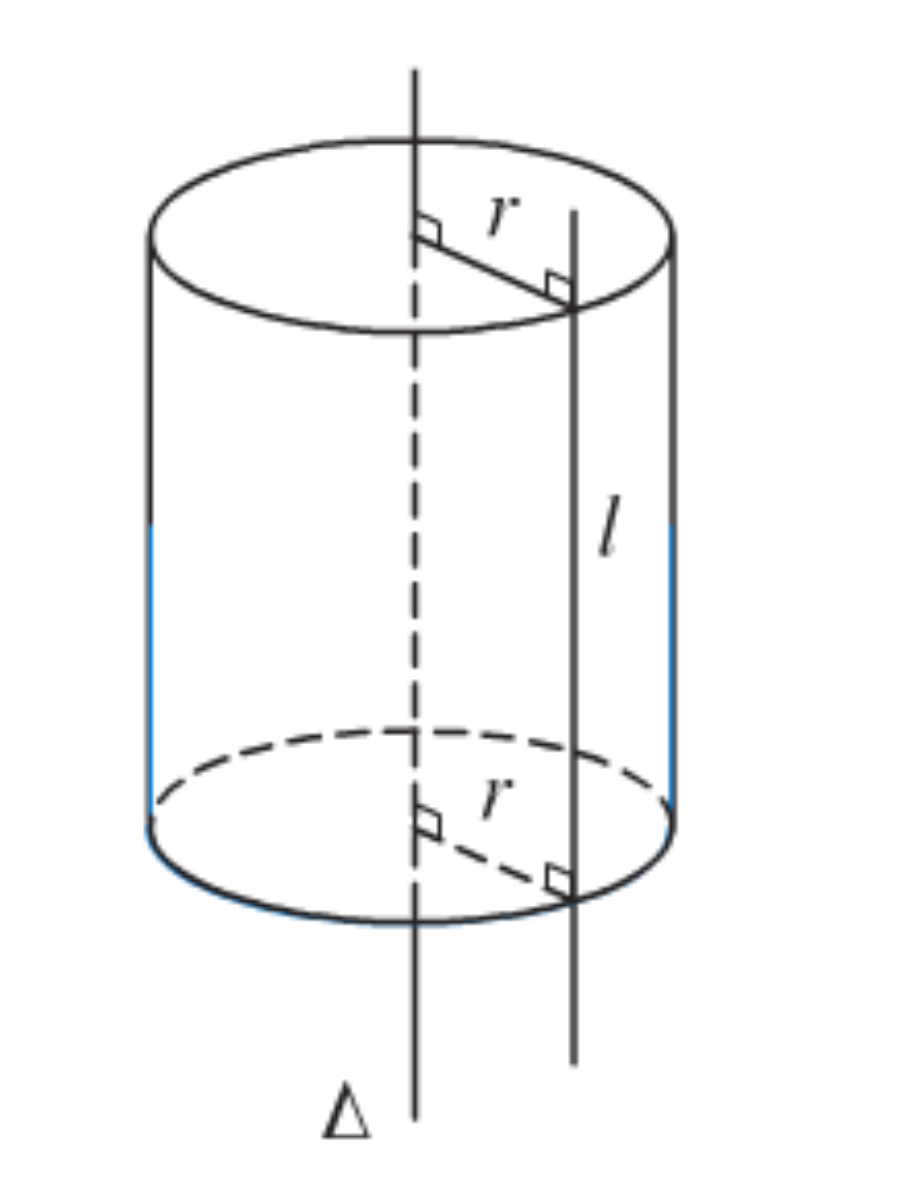
Sau đó:
- Δ được gọi là trục
- r được gọi là bán kính
- l được gọi là đường sinh
Nói cách khác, tập hợp tất cả các điểm cách đường thẳng một khoảng cố định Δ = một khoảng R không đổi được gọi là một hình trụ.
2. Định nghĩa hình trụ
Hình trụ là hình sinh ra khi quay hình chữ nhật 1 vòng quanh 1 cạnh cố định của hình chữ nhật đó. Khi đó, hình trụ giới hạn bởi hình trụ và 2 hình tròn bằng nhau có:
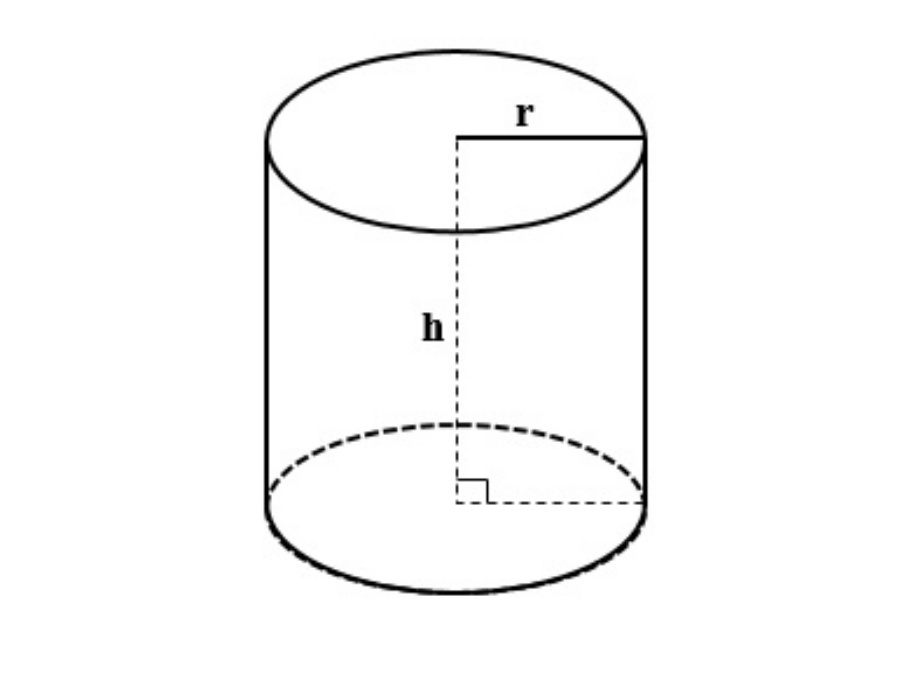
- r là bán kính
- h là chiều cao, vuông góc với hai đáy
- Đáy của hình trụ là 2 hình tròn bằng nhau
3. Định nghĩa hình trụ
Một hình trụ được định nghĩa là một hình trụ có phần bên trong của nó và thể tích của hình trụ là lượng không gian mà hình trụ chiếm.
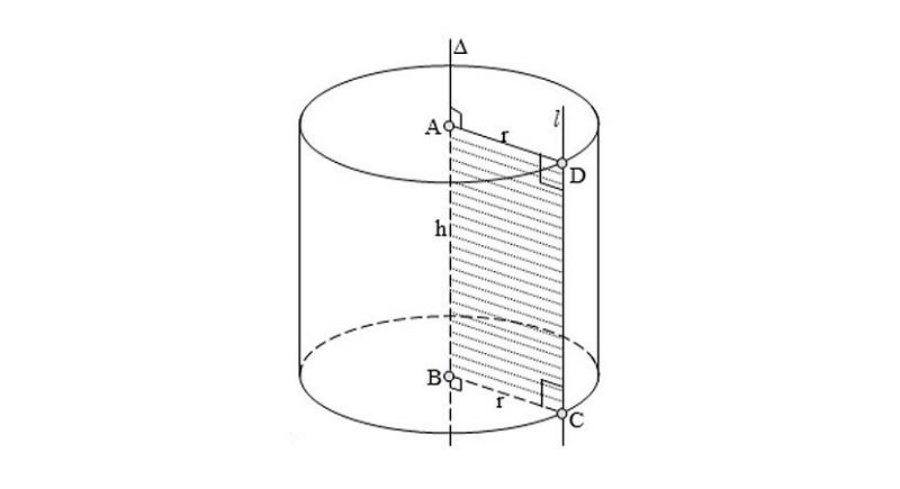
II. Công thức tính thể tích hình trụ
thể tích hình trụ là thể tích khi diện tích đáy được xếp chồng lên toàn bộ chiều cao của hình trụ và nó cũng là lượng không gian bị chiếm bởi hình trụ.
* Công thức tính thể tích khối trụ (hình trụ)
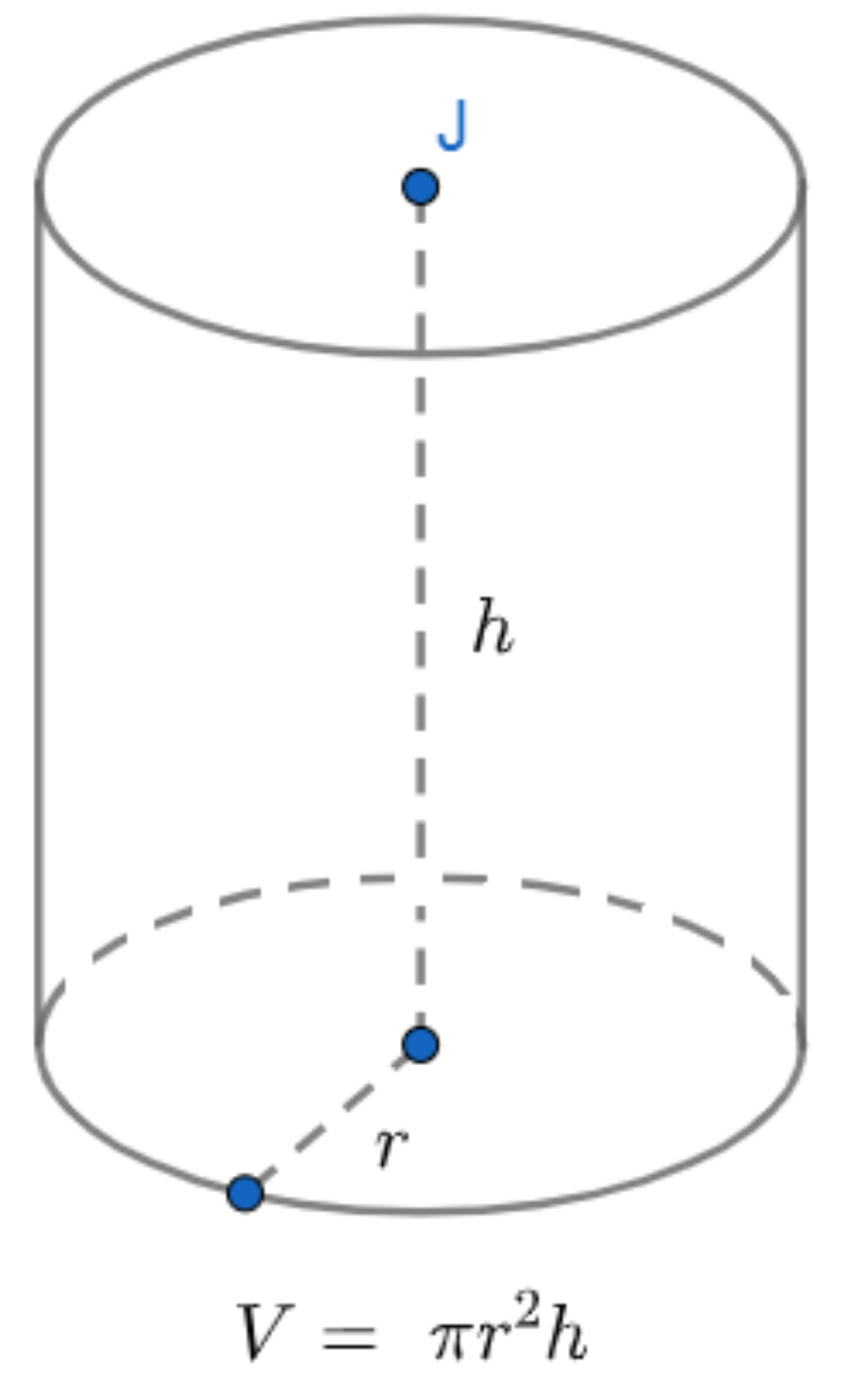
Trong đó:
- r: bán kính hình trụ
- H: chiều cao hình trụ
- π (số pi): gần 3,14
III. Hướng dẫn cách tính thể tích khối trụ
Bước 1: Đầu tiên, tìm bán kính cơ sở
Do 2 mặt đáy bằng nhau nên có thể chọn 1 mặt đáy bất kỳ để tính. Sau đó, nếu bạn đọc chủ đề, nếu nó cung cấp cho bạn bán kính, bạn có thể tiến hành bước tiếp theo. Nhưng nếu chủ đề không cung cấp cho bạn bán kính:
- Trường hợp 1: Bạn dùng thước đo khoảng cách rộng nhất trên hình tròn rồi chia kết quả cho 2 sẽ ra kết quả bán kính
- Trường hợp 2: Để cung cấp cho bạn đường kính có sẵn, bạn chỉ cần chia đường kính cho 2 để có bán kính.
- Trường hợp 3: Nếu bạn đã có sẵn chu vi, sau đó bạn chia chu vi cho 2π để có được số đo bán kính.

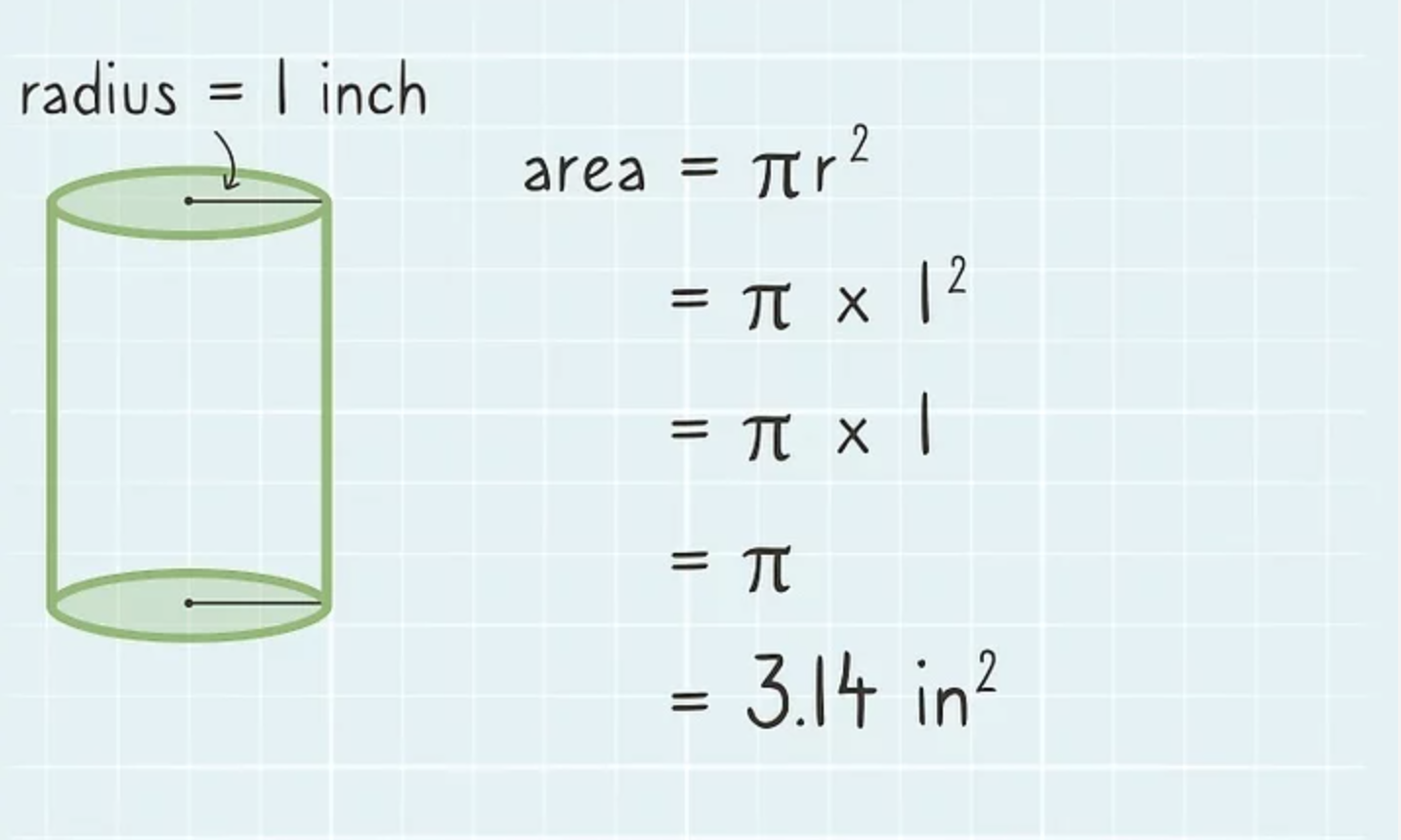
Bước 2: Tiếp theo tính diện tích đáy hình tròn
Tiếp theo, bạn thay số đo bán kính vào công thức tính diện tích hình tròn: một = r2. Giả sử hình tròn có bán kính 2,5 cm, thì bạn nhận được:
- Một = x 2,52 = π x 6,25.
- Vì là xấp xỉ 3,14 khi làm tròn đến 2 chữ số thập phân nên bạn có diện tích hình tròn đáy là 19,63 cm2
Bước 3: Sau đó tìm chiều cao của hình trụ
Tại thời điểm này, nếu vấn đề cho biết chiều cao, bạn chuyển sang bước tiếp theo. Nếu bạn không biết chiều cao của mình, hãy dùng thước để đo.
Khi đó, chiều cao của hình trụ bằng khoảng cách của hai đáy ở mặt bên.
Ví dụ: – Bạn đo chiều cao của hình trụ là 10 cm, sau đó bạn viết 10 cm ra giấy
– Như hình ảnh ví dụ bên dưới, giá trị được lấy là 4 inch, bạn có thể tham khảo giá trị đó và ghi 4 inch ra giấy.

Bước 4: Cuối cùng, nhân diện tích đáy với chiều cao
Biết diện tích đáy của hình trụ là 19,63 cm2 và chiều cao là 10 cm, bạn chỉ cần nhân chúng lên để được thể tích của hình trụ:
V = 19,63cm2 x 10 cm = 196,3 cm3
Lưu ý: Đơn vị của bạn phải ở dạng khối lập phương vì bạn đang thực hiện phép đo trong không gian ba chiều.

IV. Một số bài tập tính thể tích khối trụ
Để tính thể tích khối trụ các em nhớ và áp dụng theo 3 bước sau:
– Bước 1: Phải biết công thức tính thể tích khối trụ, viết công thức ra giấy để dễ thay số
– Bước 2: Tìm bán kính đáy và chiều cao của hình trụ
+ TH1: Nếu bài toán được đưa ra, bạn có thể chuyển sang bước tiếp theo (áp dụng công thức)
+ TH2: Bạn dùng thước để xuất bán kính đáy, chiều cao của hình trụ
+TH3:
- Cho đường kính, chia cho một nửa để có được bán kính
- Cho chu vi, chia cho 2π để có bán kính
– Bước 3: Thay bán kính và chiều cao vừa tìm được vào công thức tính thể tích khối trụ V = x r2 x h sau đó nhấn để có kết quả chính xác.
3.1 Bài tập tính thể tích khối trụ có lời giải
Câu hỏi 1: Tính V của hình trụ, biết bán kính đáy 2 là 7,1 cm, chiều cao là 5 cm.
Phần thưởng: Ta có V=πr²h -> Vậy thể tích của hình trụ: V = 3,14 x (7,1)² x 5 = 791,437 (cm³)
câu 2: Một hình trụ có chu vi đáy là 20 cm, S xung quanh bằng 14 cm². Tính chiều cao của hình trụ và thể tích của hình trụ?
Phần thưởng: Chu vi đáy của hình trụ là chu vi hình tròn = 2rπ = 20 cm. Từ đó suy ra diện tích xung quanh của hình trụ: Sxq = 2πrh = 20 xh = 14 → h = 14/20 = 0,7 (cm) -> 2rπ = 20 -> r ~ 3,18 cm
Thể tích xi lanh: V = r² xh ~ 219,91 cm³
câu 3: Một hình trụ có S xung quanh là 20π cm² và tổng S là 28π cm². Thể tích của khối trụ đó là bao nhiêu?
Phần thưởng: Diện tích toàn phần của hình trụ: Stp = Sxq + Sđ = 2πrh + 2πr² -> 2πr² = 28π – 20π = 8π -> r = 2cm
Diện tích xung quanh hình trụ là Sxq = 2πrh
<=> 20π = 2π.2.h
<=> h = 5cm
Thể tích của hình trụ là V = r²h = .22,5 = 20π cm³
câu 4: Cho một hình trụ có đáy là đường tròn ngoại tiếp tam giác đều cạnh a. Chiều cao của hình trụ là 3a. Tính thể tích của khối trụ đã cho.
Phần thưởng:
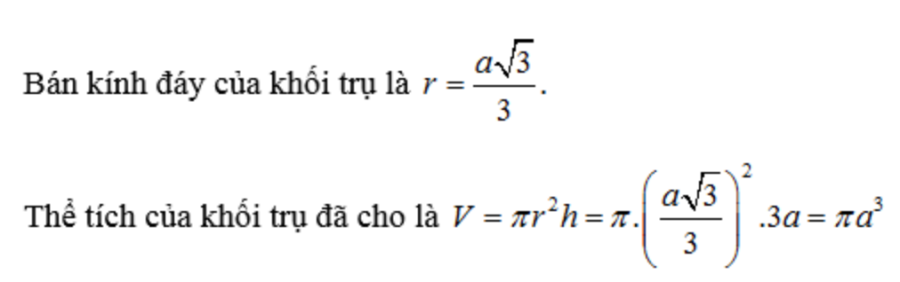
câu hỏi 5: Hình trụ có thể tích V=12π và chu vi một đáy là C=2π. Tính chiều cao của hình trụ đã cho.
Phần thưởng:
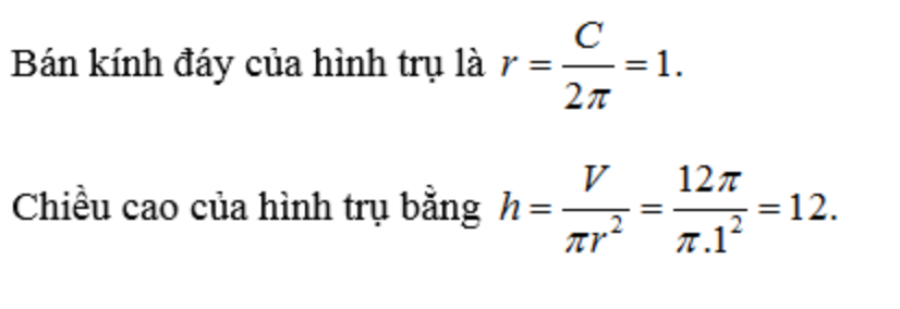
Câu 6: Cho một hình trụ có thể tích πa³ và chiều cao 2a. Tính bán kính đáy của hình trụ.
Phần thưởng:
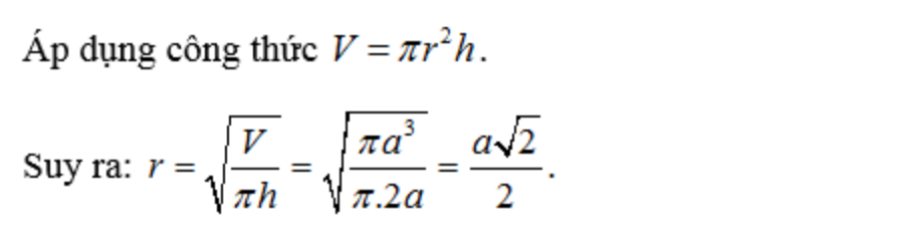
3.2 Bài tập tính thể tích khối trụ không lời giải
Câu hỏi 1: Cho lăng trụ đứng tam giác đều có cạnh bên bằng 3a. Tính thể tích của khối lăng trụ đều này.
Câu 2: Cho một hình trụ có đáy là đường tròn ngoại tiếp tam giác đều cạnh a. Chiều cao của hình trụ là 4a. Tính thể tích của khối trụ đã cho.
Câu 3: Một bể nước hình trụ có diện tích đáy B = 3 m2, chiều cao h = 2 m. Thể tích của bể nước này là bao nhiêu?
Câu 4: Hình trụ có thể tích V=14π và chu vi một đáy là C=3π . Chiều cao của hình trụ đã cho là bao nhiêu?
Câu 5: Cho lăng trụ đứng ABC A’B’C’ có đáy ABC là tam giác đều cạnh a = 3 cm, chiều cao h = 4 cm. Tính thể tích của khối lăng trụ đã cho?
Câu 6: Cho hình trụ (H) có bán kính đáy là 5 cm và chiều cao bằng đường kính đáy. Tính thể tích của khối trụ đã cho.
Câu 7: Cho một hình trụ có thể tích π x a³ và chiều cao 4a. Bán kính của đáy của hình trụ là gì?
Câu 8: Tìm thể tích của lăng trụ tam giác đều có cạnh đáy bằng 5a và cạnh bên = a
Trên đây là Công thức thể tích hình trụ & cách tính thể tích hình trụ đơn giản, nhanh chóng mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này bạn hoàn toàn có thể tính được thể tích Xi lanh một cách dễ dàng. Nếu có bất kỳ thắc mắc nào, bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc may mắn.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%

