Đường trung trực là một trong những kiến thức Toán học quan trọng trong chương trình Toán 7, 8. Tuy nhiên, đến giờ nhiều bạn vẫn chưa biết được đường trung trực là gì, tính chất đường trung trực và làm sao để giải được các bài tập về đường trung trực.
Đừng lo, đội ngũ INVERT chúng tôi sẽ hướng dẫn bạn biết được đường trung trực là gì, tính chất, dấu hiệu nhận biết đường trung trực, cách giải các bài tập đường trung trực vô cùng đơn giản, chi tiết, dễ hiểu thông qua bài viết sau.
Mục lục bài viết [Ẩn]
I. Đường Trung Trực là gì?
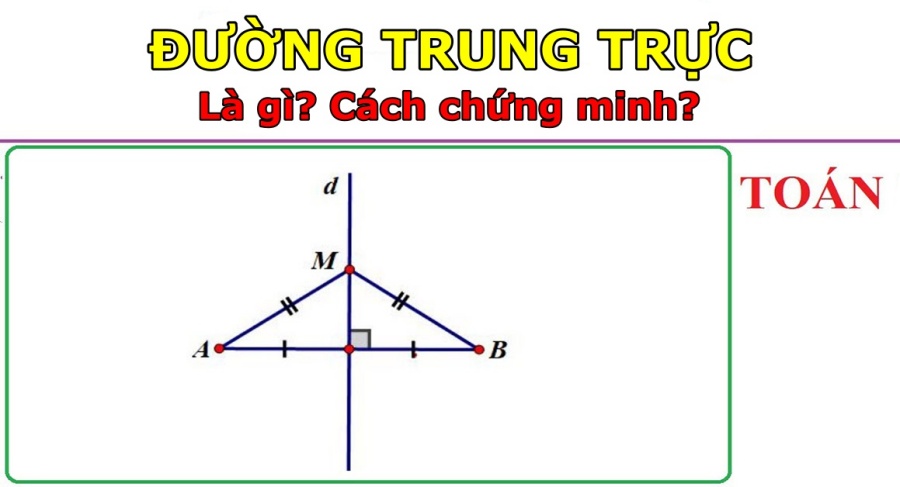
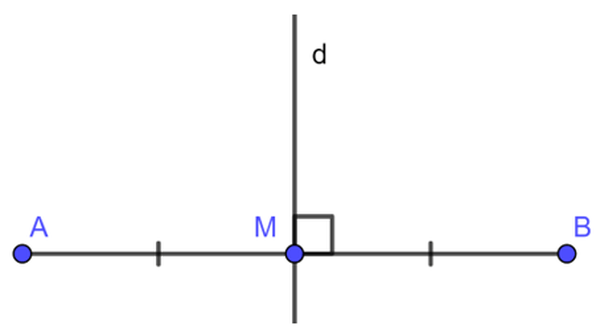
Định nghĩa: Trong hình học phẳng, đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Ví dụ: d là đường trung trực của đoạn thẳng AB vì M là trung điểm của AB và d vuông góc với AB tại M.
Đường trung trực của tam giác là gì?
Định nghĩa: Đường trung trực của mỗi cạnh của tam giác gọi là đường trung trực của tam giác.
Tính chất:
- Trong tam giác 3 đường trung trực đồng quy tại 1 điểm. Điểm đó cách đều 3 đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác.
- Trong tam giác vuông tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
- Trong tam giác cân, đường trung trực của cạnh đáy cũng là đường trung tuyến, đường phân giác, đường cao tương ứng của đỉnh đối diện với cạnh này.
- Trong không gian 3 chiều, quỹ tích này mở rộng thành mặt phẳng trung trực của đoạn thẳng.
Cách vẽ đường trung trực
– Bằng compa: Quay 2 đường tròn có tâm là 2 đầu đoạn thẳng với bán kính bằng độ dài đoạn thẳng (hoặc ít nhất là lớn hơn nửa độ dài đoạn thẳng). Khi đó, đường trung trực là đường nối giao điểm 2 đường tròn này.
– Bằng thước và êke: Tiến hành kẻ đường thẳng vuông góc với đoạn thẳng cần vẽ đường trung trực tại trung điểm của nó.
II. Tính chất đường trung trực
Tính chất đường trung trực là gì?
1. Tính chất đường trung trực của một đoạn thẳng
Cho hình vẽ, d là đường trung trực của đoạn thẳng AB.
Ta nói: A đối xứng với B qua d.
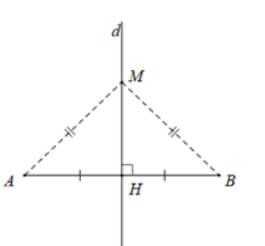
– Định lý 1 (định lí thuận): Điểm nằm trên đường trung trực của 1 đoạn thẳng thì cách đều 2 mút của đoạn thẳng đó.
Giả sử: d là trung trực của AB, M ∈ d
=> MA = MB
– Định lí 2 (định lí đảo): Điểm cách đều 2 đầu mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó
Giả sử: Chứng minh được MA = MB => M thuộc đường trung trực của AB
Nhận xét: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
2. Tính chất ba đường trung trực của tam giác
Tính chất: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó
Cho hình vẽ, điểm O là giao điểm các đường trung trực của ΔABC.
Ta có OA = OB = OC. Điểm O là tâm đường tròn ngoại tiếp ΔABC
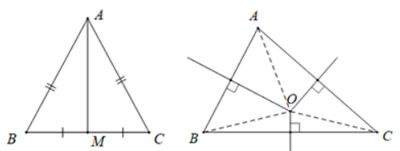
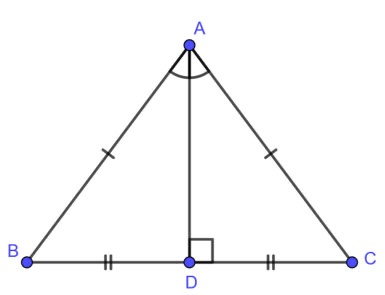
3. Tính chất đường trung trực của tam giác cân
Trong tam giác cân, đường trung trực ứng với cạnh đáy còn được gọi là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.
4. Tính chất đường trung trực của tam giác vuông
Trong tam giác vuông, trung điểm của cạnh huyền chính là giao điểm của 3 đường trung trực. Tam giác ABC vuông tại B, giao điểm của 3 đường trung trực là trung điểm E của cạnh huyền AC.
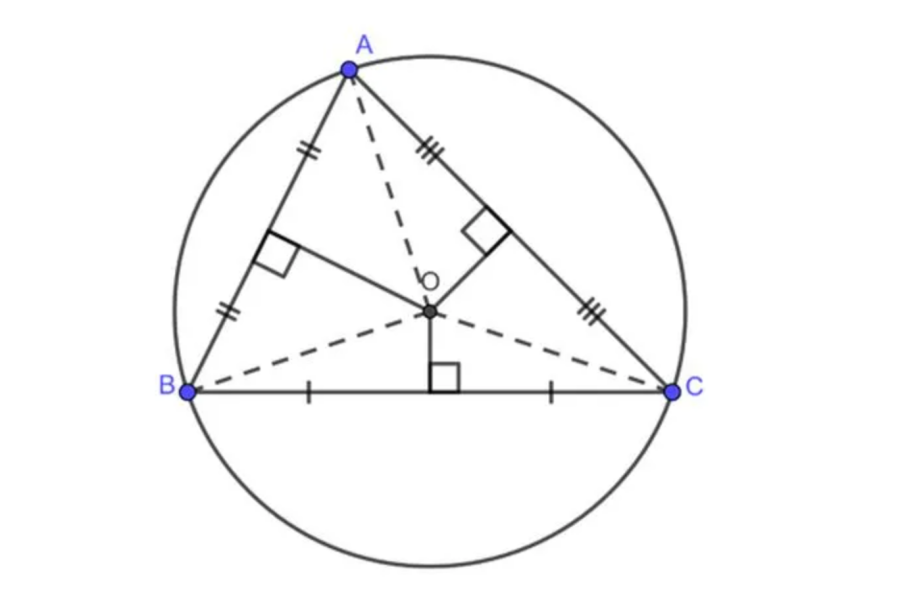
5. Tính chất đường trung với đường tròn ngoại tiếp tam giác
Áp dụng tính chất giao điểm 3 đường trung trực của tam giác: Giao điểm của ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác đó. O là giao điểm của ba đường trung trực của tam giác ABC. Khi đó, O là tâm đường tròn ngoại tiếp tam giác ABC.
Định lý: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
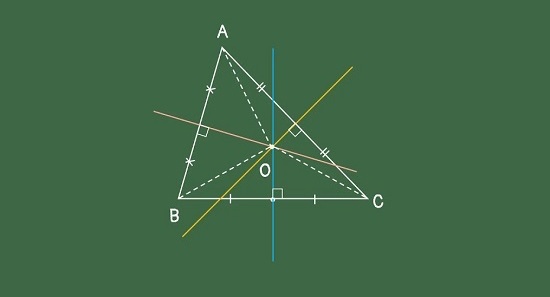
III. Cách chứng minh đường trung trực
Có 5 phương pháp để chứng minh d là trung trực của đoạn thẳng AB:
- Phương pháp 1: Chứng minh d vuông góc AB tại trung điểm AB
- Phương pháp 2: Chứng minh 2 điểm trên d cách đều 2 điểm A và B
- Phương pháp 3: Dùng tính chất đường trung tuyến, đường cao
- Phương pháp 4: Áp dụng tính chất đối xứng của trục
- Phương pháp 5: Áp dụng tính chất đoạn nối tâm của 2 đường tròn cắt nhau ở 2 điểm.
IV. Các dạng bài tập chứng minh đường trung trực
Cách chứng minh đường trung trực lớp 6, 7, 8 thường có nhiều yêu cầu khác nhau nhưng nhìn chung thì sẽ có 5 dạng cơ bản sau:
– Dạng 1: Chứng minh rằng 2 đoạn thẳng bằng nhau.
Cách giải: Áp dụng định lý khi 1 điểm nằm trên đường trung trực của đoạn thẳng thì sẽ sẽ cách đều 2 đầu đoạn thẳng.
Ví dụ: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt cạnh AC tại điểm D. Trên cạnh BC, lấy điểm E sao cho: BE = AB. Chứng minh rằng: AD = DE.
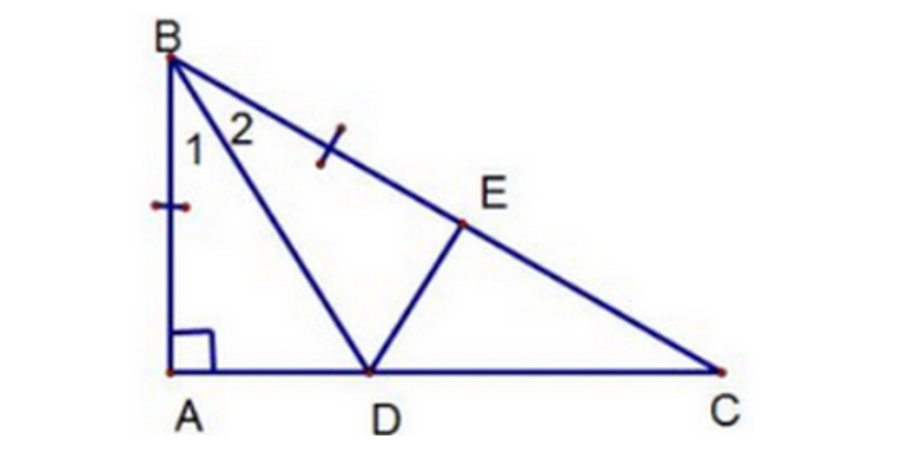
Xét tam giác ABD và tam giác EBD, có:
BD là cạnh chung
BE = AB (đề bài đã cho)
góc ABD = góc DBE (vì BD là tia phân giác của góc B)
=> Tam giác ABD = tam giác EBD (c.g.c)
=> AD = DE (điều phải chứng minh).
– Dạng 2: Chứng minh d là đường trung trực của A B (cơ bản
Cách giải: Hãy chứng minh rằng d có các điểm mà các điểm này cách đều A và B.
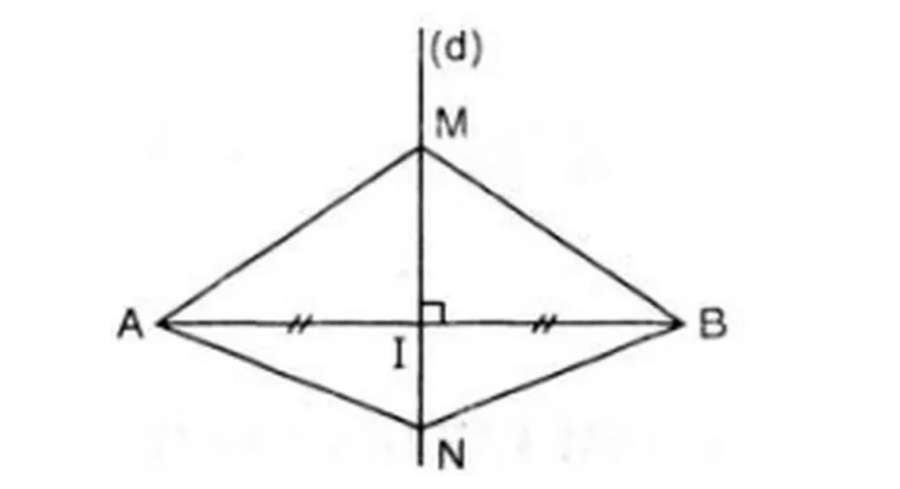
Ví dụ: Chứng minh đường thẳng PQ là đường trung trực của đoạn thẳng MN.
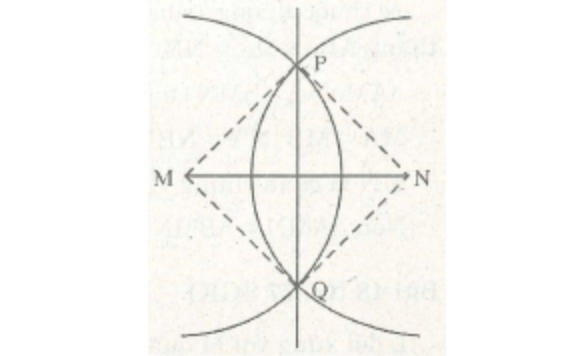
P, Q là giao điểm của hai cung tròn tâm M, N có cùng bán kính nên:
PM = PN (= bán kính cung tròn).
QM = QN (= bán kính cung tròn).
Suy ra P và Q cùng thuộc đường trung trực của đoạn thẳng MN.
Vậy PQ là đường trung trực của đoạn thẳng MN.
– Dạng 3: Tìm tâm đường tròn ngoại tiếp của tam giác.
Cách giải: Áp dụng tính chất giao điểm đường trung trực của tam giác.
– Dạng 4: Đường trung trực trong tam giác cân.
Cách giải: Chúng ta phải hiểu rằng đối với tam giác cân, đường trung trực cạnh đáy cũng là đường trung tuyến tương ứng với cạnh đấy đó.
Ví dụ : Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Giải: Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
– Dạng 5: Tìm giá trị nhỏ nhất
Cách giải: Áp dụng định lý bất đẳng thưc trong tam giác.
Ví dụ: Cho hình bên, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho đường thẳng a là trung trực của AC.
a) Hãy so sánh MA + MB với BC.
b) Tìm vị trí của điểm M trên đường thẳng a để MA + MB là nhỏ nhất.
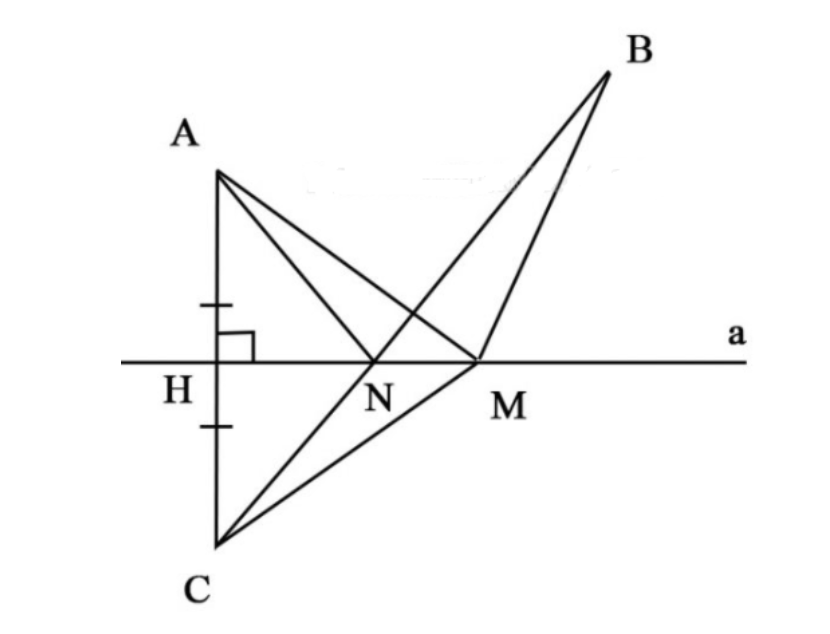
Giải:
a) Gọi H là giao điểm của a với AC
∆MHA = ∆MHC (c.g.c) => MA = MC.
Do đó:
MA + MB = MC + MB.
Gọi N là giao điểm của đường thẳng a với BC (chứng minh được NA = NC).
Nếu M không trùng với N thì:
MA + MB = MC + MB > BC (bất đẳng thức trong ∆BMC).
Nếu M trùng với N thì :
MA + MB = NA + NB = NC + NB = BC.
Vậy MA + MB ≥ BC.
b) Từ câu a) ta suy ra : Khi M trùng với N thì tổng MA + MB là nhỏ nhất.
– Dạng 6: Bài toán liên quan đến đường trung trực đối với tam giác vuông
Cách giải: Áp dụng định lý trong tam giác vuông, giao điểm các đường trung trực là trung điểm cạnh huyền
Ví dụ 1: Cho tam giác ABC vuông tại B có AB = 6cm, BC = 8cm. Gọi E là giao điểm của ba đường trung trực của tam giác ABC. Tính độ dài khoảng cách từ E đến ba đỉnh của tam giác ABC?
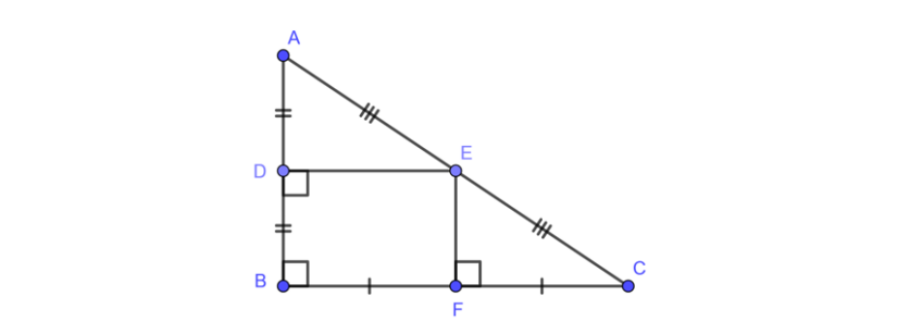
Giải: Vì E là giao điểm của ba đường trung trực của tam giác ABC nên ta có:
EA = EB = EC
Mà tam giác ABC vuông tại B nên E là trung điểm của AC
Áp dụng định lí Pytago vào tam giác ABC ta được:
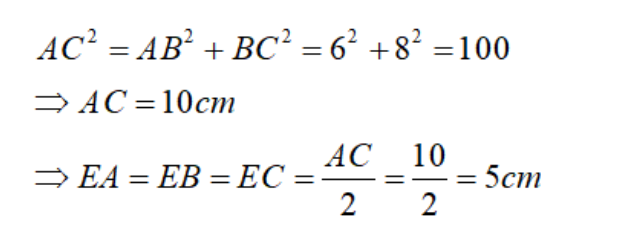
V. Một số bài tập về đường trung trực
1. Bài tập đường trung trực có lời giải
Bài 1: Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Giải: Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
Bài 2: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là t am giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
Giải: Giả sử ΔABC có AM là trung tuyến đồng thời là đường trung trưc. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (gt) ⇒ BM = MC (tính chất trung tuyến)
Vì AM là trung trực của BC ⇒ AM ⊥ BC
Xét hai tam giác vuông ΔABM và ΔACM có:
BM = CM (cmt)
AM chung
⇒ ΔABM = ΔACM (2 cạnh góc vuông)
⇒ AB = AC (2 cạnh tương ứng) ⇒ ΔABC cân tại A
Chọn đáp án D
Bài 3: Cho tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE = AB. Chứng minh rằng AD vuông góc với BE.
Giải:
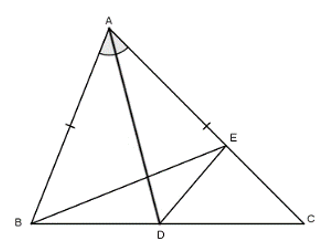
Nối BE và ED
Xét ΔADB và ΔADE có:
AD cạnh chung
∠BAD = ∠EAD (AD là tia phân giác góc BAC)
AB = AE (gt)
Do đó: ∠ADB = ∠ADE (c-g-c)
Suy ra DB = DE
Lại có AB = AE (gt)
Do đó AD là đường trung trực của BE
Hay AD vuông góc với BE
Bài 4: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Nếu MA có độ dài 5cm thì độ dài MB bằng bao nhiêu?
Giải: Vì điểm M nằm trên đường trung trực của đoạn thẳng AB nên theo định lí về tính chất của các điểm thuộc đường trung trực ta có MA = MB. Mà MA = 5cm (gt) suy ra MB = 5cm.
Bài 5: Chứng minh đường thẳng PQ được vẽ như trong hình đúng là đường trung trực của đoạn thẳng MN.
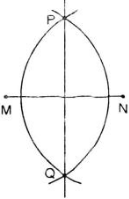
Giải:
Ta có : Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
⇒ P; Q cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.
Bài 6: Cho đoạn thẳng AB thuộc nửa mặt phẳng bờ d. Xác định điểm M thuộc d sao cho M cách đều hai điểm A, B.
Giải: Vẽ trung trực xy của đoạn thẳng AB
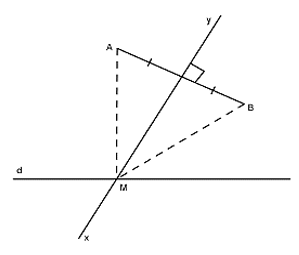
Giả sử xy cắt d tại điểm M, ta có: MA = MB
+ Nếu AB ⊥ d thì xy // d, ta không xác định được điểm M
+ Ngoài trường hợp AB ⊥ d , ta luôn xác định được điểm M và M là duy nhất.
Bài 7: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Vẽ đường trung trực của các cạnh AB, AC cắt BC lần lượt tại D và E. Các tam giác ABD và AEC là tam giác gì?
Giải:
Vì DM là đường trung trực của cạnh AB nên DA = DB
Suy ra, tam giác ADB cân tại D.
Vì EN là đường trung trực của cạnh AC nên EA = EC
Suy ra, tam giác AEC cân tại E.
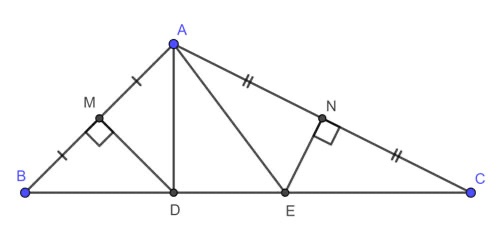
2. Bài tập đường trung trực không có lời giải
Bài 1: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
Bài 2: Cho ΔABC vuông tại A, có ∠C = 30°, đường trung trực của BC cắt AC tại M. Em hãy chọn câu đúng:
A. BM là đường trung tuyến của ΔABC
B. BM = AB
C. BM là phân giác của ∠ABC
D. BM là đường trung trực của ΔABC
Bài 3: Cho điểm C thuộc trung trực của đoạn thẳng AB. Biết CA = 10 cm. Độ dài đoạn thẳng CB là:
A. CB = 10 cm
B. CB = 20 cm
C. CB = 30 cm
D. CB = 40 cm
Bài 4: Cho ΔABC cân tại A , có ∠A = 40°, đường trung trực của AB cắt BC tại D . Tính ∠CAD
A. 30°
B. 45°
C. 60°
D. 40°
Bài 5. Cho đoạn thẳng AB. Gọi O là trung điểm của AB. Trong hai nửa mặt phẳng bờ là đường thẳng AB lấy hai điểm M và N sao cho MA = MB và NA = NB.
A. Đường thẳng MN đi qua O
B. Đường thẳng MN vuông góc với AB
C. Đường thẳng MN vuông góc với AB tại O
D. Đường thẳng MN song song với AB
Bài 6: Trên đường thẳng d là trung trực của đoạn thẳng AB lấy điểm M, N nằm ở hai nữa hai mặt phẳng đối nhau có bờ là đường thẳng AB.
a) Chứng minh góc MAN = góc MBN
b) MN là tia phân giác của AMB.
Bài 7: Cho 2 điểm A và B nằm trên cùng một mặt phảng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đường thẳng BC, AC cắt d tai E. Trên d lấy điểm M bất kỳ.
a) So sánh MA + MB và AC
b) Tìm vị trí của M trên d để MA + MB ngắn nhất
Bài 8: Cho tam giác ABC vuông tại A ,đương cao AH. Vẽ đường trung trục của cạnh AC cát BC tai I và cát AC tai E.
a) Chúmg minh IA = IB = IC.
b) Goi M là trung điểm của đoạn AI, chứng minh MH = ME
c) BE cắt AI tại N, tính tỉ số của đoạn MN và AI
Bài 9: Cho tam giác ABC cân tại A. Hai trung tuyến BM, CN cắt nhau tại I. Hai tia phân giác trong của góc B và C cắt nhau tại O.Hai đường trung trực của 2 cạnh AB và AC cắt nhau tại K.
a) Chứng minh: BM = CN.
b) Chứng minh OB = OC
c) Chứng minh các điểm A,O, I, K thẳng hàng.
Bài 10: Cho góc xOy = 50, điểm A nằm trong góc xOy. Vẽ điềm M sao cho Ox là trung trực của đoạn AN, vẽ điểm M sao cho Oy là trung trực của đoạn AM.
a) Chứng minh: OM = ON
b) Tính số đo góc MON
Bài 11: Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự ở D và E.
a) Các tam giác ABD, ACE là tam giác gì.
b) Đường tròn tâm O bán kinh OA đi qua những điểm nào trên hình vẽ?
Bài 12: Cho 4 điểm A, B, C, D phân biệt. Với điều kiện nào sau đây thì đường thẳng AC là đường trung trực của đoạn thẳng BD ?
Bài 13: Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆AMN = ∆BMN
Bài 14: Cho ba tam giác ABC, DBC, EBC có chung đáy BC . Chứng minh 3 điểm A, D, E thẳng hàng
Bài 15: Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Cho MA =5cm. Hỏi độ dài MB bằng ?
3. Chứng minh đường trung trực lớp 7 có lời giải
Bài 44 (trang 76 SGK Toán 7 tập 2): Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu?
Giải: Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Kiến thức áp dụng: Dựa vào định lí về tính chất của các điểm thuộc đường trung trực (định lý thuận): Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Bài 45 (trang 76 SGK Toán 7 tập 2): Chứng minh đường thẳng PQ được vẽ như trong hình đúng là đường trung trực của đoạn thẳng
Giải: Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
=> P; Q cách đều hai mút M, N của đoạn thẳng MN
Nên theo định lí 2 : P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.
Bài 46 (trang 76 SGK Toán 7 tập 2): Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Giải: Vì ΔABC cân tại A AB = AC
=> A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D DB = DC
=> D thuộc đường trung trực của BC
Vì ΔEBC cân tại E EB = EC
=> E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
Bài 47 (trang 76 SGK Toán 7 tập 2): Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
Giải:
Vì M thuộc đường trung trực của AB
=> MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
=> NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
ΔAMN = ΔBMN (c.c.c)
Bài 48 (trang 77 SGK Toán 7 tập 2): Hai điểm M và N cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Giải: Vì L và M đối xứng qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML.
Nên đường thẳng xy là trung trực của ML.
I xy => IM = IL (theo định lý 1).
Nên IM + IN = IL + IN
TH1: Nếu I, L, N thẳng hàng
=> IL + IN = LN (vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy).
=> IM + IN = LN
TH2: Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàng
Áp dụng bất đẳng thức tam giác vào Δ INL ta được: IL + IN > LN
mà IM = IL (cmt)
=> IL + IN > LN (bất đẳng thức tam giác)
=> IM + IN > LN
Vậy với mọi vị trí của I trên xy thì IM + IN LN
Bài 49 (trang 77 SGK Toán 7 tập 2): Hai nhà máy được xây dựng bên bờ một con sông tại hai địa điểm A và B (h.44). Hãy tìm trên bờ sông một địa điểm C để xây dựng một trạm bơm đưa nước về cho hai nhà máy sao cho độ dài đường ống dẫn nước là ngắn nhất?
Giải: Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
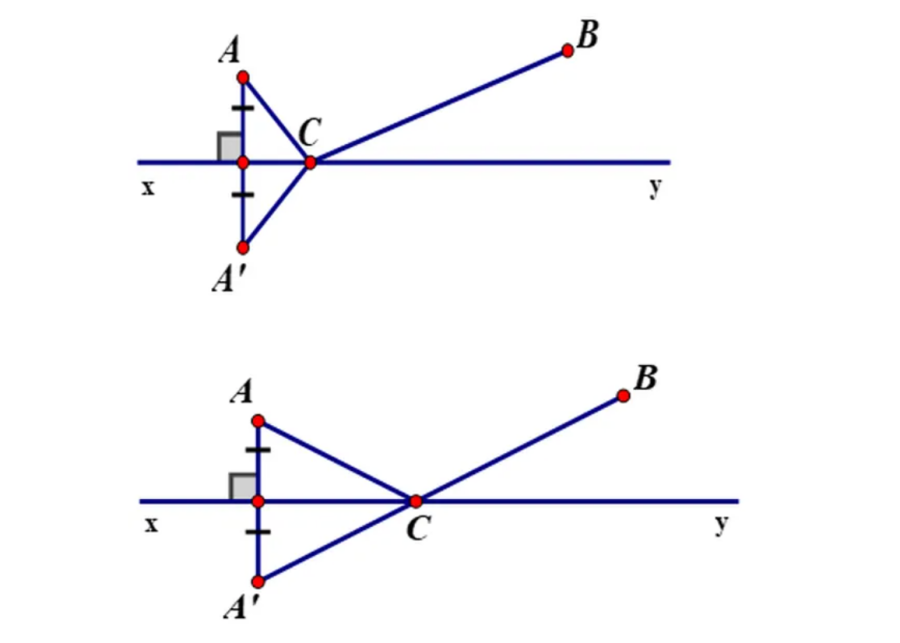
=> Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
Gọi A là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA + CB AB (AB cố định).
=> CA + CB đạt ngắn nhất bằng AB.
Dấu = xảy ra khi CA+CB = AB, tức là A; B; C thẳng hàng hay C là giao điểm của AB và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng AB, trong đó A là điểm đối xứng với A qua xy
Bài 51 (trang 77 SGK Toán 7 tập 2): Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Giải:
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC d.
b) Một cách vẽ khác
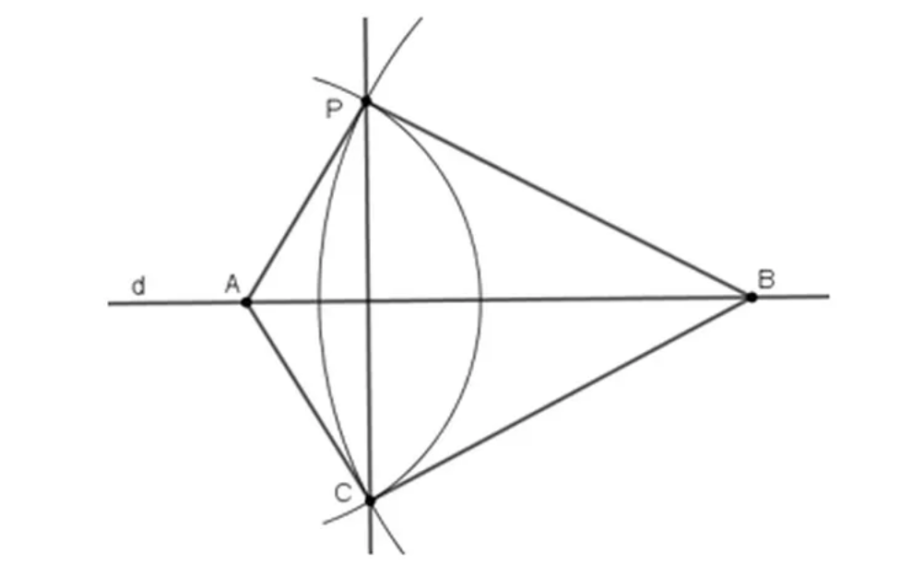
Lấy hai điểm A, B bất kì trên d.
Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d
Chứng minh :
Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
=> A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
=> B thuộc đường trung trực của PC.
=> AB là đường trung trực của PC
=> PC AB hay PC d.
4. Cách chứng minh đường trung trực lớp 8 & bài tập có lời giải
Bài 1: Tìm vectơ pháp tuyến, cho A(1;-4) và B(3;2), viết pt tổng quát đường trung trực của đoạn AB.
Giải:
Vectơ AB = (3 1 ; 2 (-4)) = (2; 6) = 2 (1; 3)
=> Vectơ pháp tuyến của đường trung trực của đoạn AB là : Vectơ n = (1; 3)
Gọi I(x;y ) là trung điểm của AB
x = (1 + 3 ) / 2 = 2
Và y = (- 4 + 2)/ 2 = -1
=> I(2; -1)
Phương trình tổng quát đường trung trực của đoạn AB :
a(x x0) + b(y y0 ) = 0
<=> x 2 + 3(y + 1 ) = 0
=> x + 3y + 1 = 0
Bài 2: Cho hai điểm A(1;0) và B(1;2). Viết phương trình đường trung trực của đoạn thẳng AB.

Viết phương trình đường trung trực dựa trên vectơ pháp tuyến.

Trên đây là định nghĩa đường trung trực là gì, tính chất, dấu hiệu nhận biết và cách giải các bài tập đường trung trực nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể biết được đường trung trực là gì cũng như giải các bài tập về đường trung trực một cách dễ dàng. Nếu có gì thắc mắc bạn cũng có thể bình luận bên dưới, chúng tôi sẽ giải đáp cho bạn. Chúc các bạn thành công.
Tags:
tính chất đường trung trực là gìđịnh nghĩa đường trung trực của đoạn thẳngcách chứng minh đường trung trực

