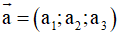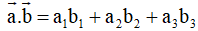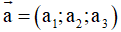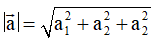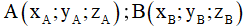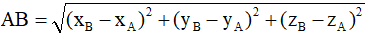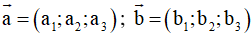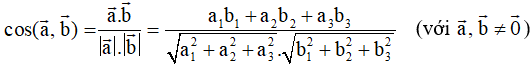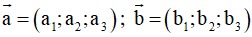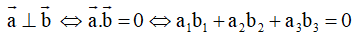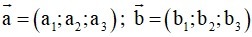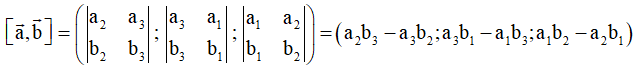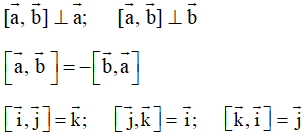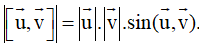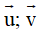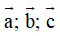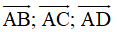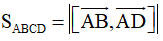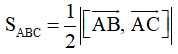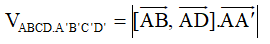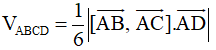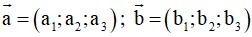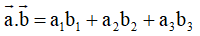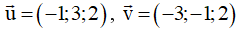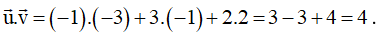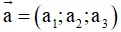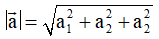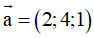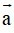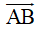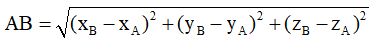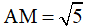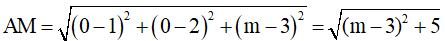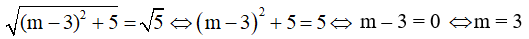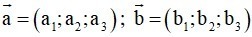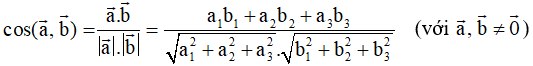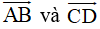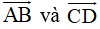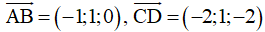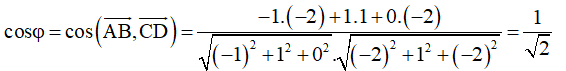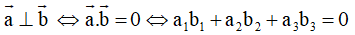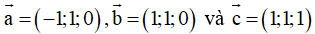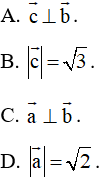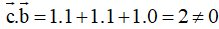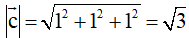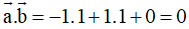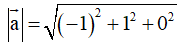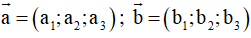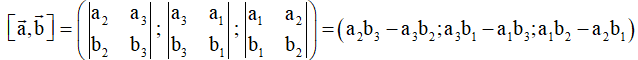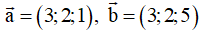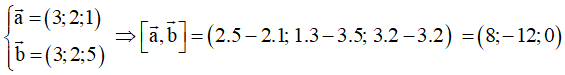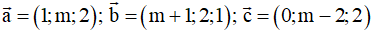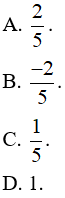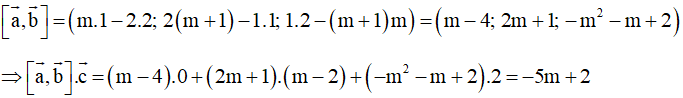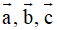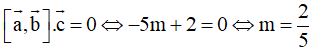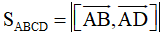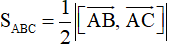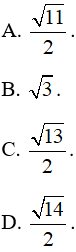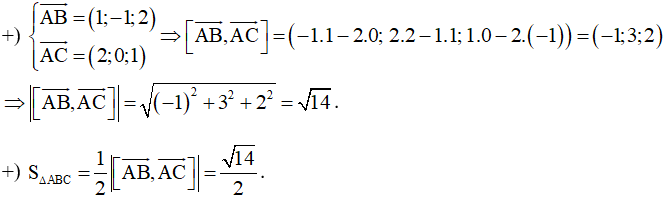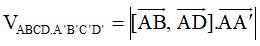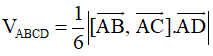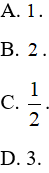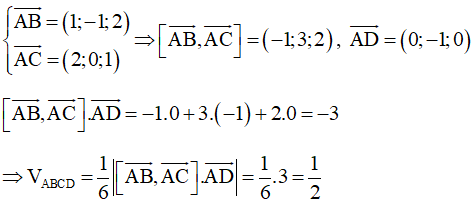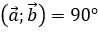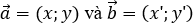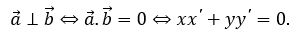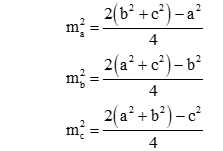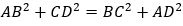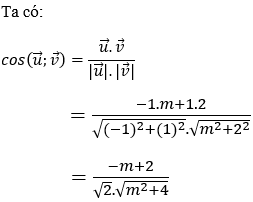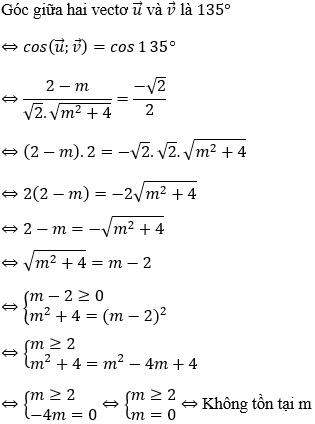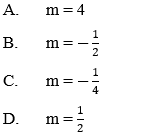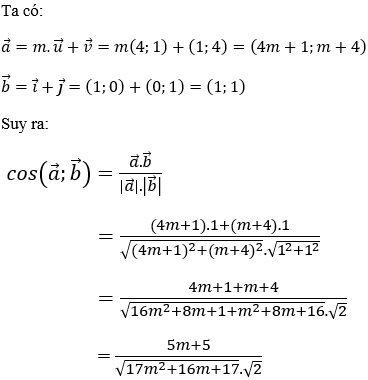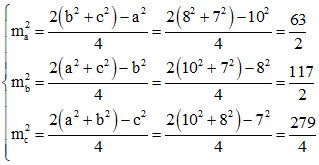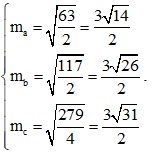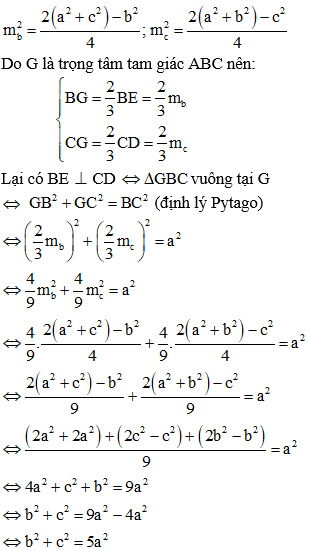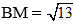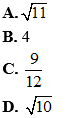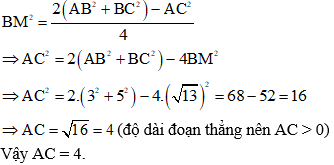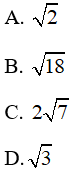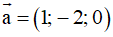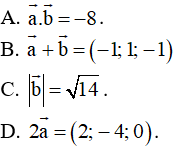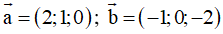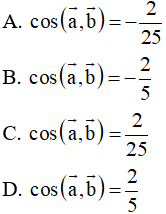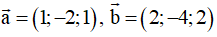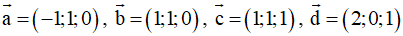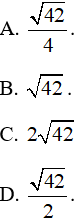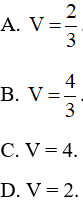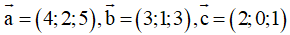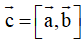Giải bài tập tích có hướng, tích vô hướng của hai vectơ

1. Tích vô hướng và tích có hướng của hai vecto:

1.1. Tích vô hướng của hai vectơ:

a) Tích vô hướng của hai vectơ

Trong không gian Oxyz, tích vô hướng của hai vectơ 

 và 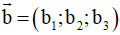 được xác định bởi công thức:

b) Ứng dụng của tích vô hướng

+ Cho vectơ 

, khi đó độ dài của vectơ 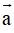 được tính theo công thức:

+ Cho hai điểm

. Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ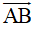. Do đó ta có

+ Cho vectơ

. Khi đó góc giữa hai vectơ  và  được tính theo công thức:

+ Hai vectơ vuông góc: Cho vectơ 

. Khi đó: 

1.2. Tích có hướng của hai vectơ:

a) Tích có hướng của hai vectơ

Trong không gian Oxyz cho hai vectơ

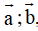
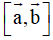
 . Tích có hướng của hai vectơkí hiệu là , được xác định bởi

Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

b) Tính chất của tích có hướng:

+ Độ dài của vectơ tích có hướng 

+ Hai vectơ 

 cùng phương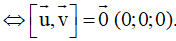

+ Ba vectơ 

 đồng phẳng khi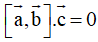 

Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ

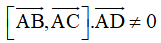
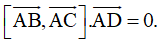
không đồng phẳng hay  và 4 điểm A, B, C, D đồng phẳng khi 

1.3. Ứng dụng của tích có hướng:

Ta sử dụng tích có hướng để tính:

+) Diện tích hình bình hành ABCD: 

+) Diện tích tam giác ABC:

+) Thể tích khối hộp ABCD.A’B’C’D’: 

+) Thể tích tứ diện ABCD:

2. Phương pháp giải và ví dụ minh hoạ:

2.1. Tích vô hướng của hai vectơ:

Dạng 1: Tính biểu thức tọa độ tích vô hướng

Phương pháp giải: Cho hai vectơ

khi đó:

Ví dụ 1: Trong không gian Oxyz, cho

.Khi đó 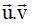 bằng

A. 10

B. 2

C. 3

D. 4

Hướng dẫn giải

Chọn D.

Dạng 2: Tính độ dài của một vectơ

Phương pháp giải: Cho vectơ 

 , khi đó độ dài của vectơ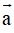được tính theo công thức:

Ví dụ 2: Trong không gian Oxyz cho vectơ

. Độ dài vectơ 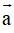là

A. 

B. 

C. 21

D. 7

Hướng dẫn giải:

Độ dài vectơ

là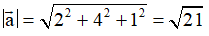

Chọn A.

Dạng 3: Khoảng cách giữa hai điểm

Phương pháp giải: Cho hai điểm A (xA;yA;zA) và B (xB;yB;zB). Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ

. Do đó ta có

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3), trên trục Oz lấy điểm M sao cho 

. Tọa độ của điểm M là

A. M (0; 0; 3).

B. M (0; 0; 2).

C. M (0; 0; -3).

D. M (0; 3; 0).

Hướng dẫn giải

Do M ∈ Oz => M (0; 0; m)

. Mặt khác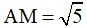nên:

Suy ra M (0; 0; 3). 

Chọn A.

Dạng 4: Góc giữa hai vectơ

Phương pháp giải: Cho vectơ 

. Khi đó góc giữa hai vectơ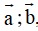được tính theo công thức:

Ví dụ 4: Trong không gian Oxyz, cho bốn điểm A (1; 0; 0), B (0; 1; 0), C (0; 0; 1) và D (-2; 1; -1). Tính góc giữa hai vectơ

.

A. 450

B. 600

C. 900

D. 1350

Hướng dẫn giải

Gọi φ là góc tạo bởi hai vectơ 

 .

Ta có:

. Khi đó: 

=> φ = 450

Chọn A.

Dạng 5: Tìm điều kiện để hai vectơ vuông góc

Phương pháp giải: Cho vectơ

. Khi đó: 

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho các vec tơ

. Mệnh đề nào dưới đây sai?

Hướng dẫn giải

Ta kiểm tra lần lượt từng đáp án:

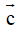
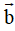
. Suy rakhông vuông góc với. Do đó A sai. 

Có thể kiểm tra thêm 3 đáp án còn lại:

. Do đó B đúng.

. Suy ra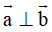 . Do đó C đúng.

. Do đó D đúng.

Chọn A.

2.2. Tích có hướng của hai vectơ:

Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.

Dạng 1: Tính tích có hướng của hai vectơ

Phương pháp giải: Cho hai vectơ 

, khi đó:

Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho

. Khi đó 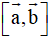có tọa độ bằng

A. (8;-12;5)

B. (8;-12;0)

C. (0;8;12)

D. (0;8;-12)

Hướng dẫn giải

Chọn B. 

Dạng 2: Tìm điều kiện để ba vectơ đồng phẳng 

Phương pháp giải:

 đồng phẳng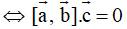

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz cho vectơ 

. Giá trị của m để 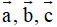 đồng phẳng là

Hướng dẫn giải

Ta có 

Để 

 đồng phẳng thì

Chọn A.

Dạng 3: Tính diện tích một số hình phẳng

Phương pháp giải:

Áp dụng các công thức sau:

+) Diện tích hình bình hành ABCD:

+) Diện tích tam giác ABC:

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A (1; 2; 1), B (2; 1; 3) và C (3; 2; 2). Diện tích tam giác ABC bằng

Hướng dẫn giải

Chọn D.

Dạng 4: Tính thể tích khối hộp và tứ diện

Phương pháp giải:

Áp dụng các công thức sau:

+) Thể tích khối hộp ABCD. A’B’C’D’:

+) Thể tích tứ diện :

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A (1; 2; 1), B (2; 1; 3), C (3; 2; 2), D (1; 1; 1). Thể tích của tứ diện ABCD bằng

Hướng dẫn giải

Chọn C.

3. Các dạng bài tập ứng dụng về tích vô hướng, có hướng:

3.1. Chứng minh hai vecto vuông góc:

Phương pháp 1: Sử dụng định nghĩa

Nếu 

 thì hai vectơ  vuông góc với nhau, kí hiệu .

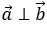
Phương pháp 2: Sử dụng tính chất của tích vô hướng và áp dụng trong hệ tọa độ

Cho 

.

Khi đó:

3.2. Tìm m để góc giữa hai vecto bằng một số cho trước (45 độ, góc nhọn, góc tù):

Các bước làm bài

3.3. Công thức, cách tính độ dài đường trung tuyến:

Áp dụng công thức tính độ dài đường trung tuyến:

Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi ma; mb; mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác. Khi đó

4. Bài tập minh hoạ và hướng dẫn giải:

Bài 1: Cho hai vectơ 

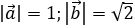
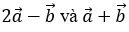
 vuông góc với nhau và . Chứng minh hai vectơ  vuông góc với nhau.

Hướng dẫn giải:

Bài 2: Cho tứ giác ABCD có 

. Chứng minh hai vectơ 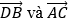 vuông góc.

Hướng dẫn giải:

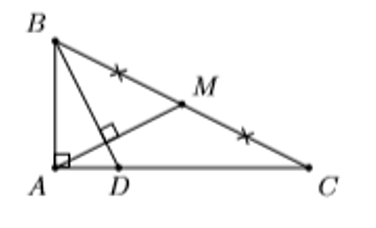
Bài 3: Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC và điểm D bất kỳ thuộc cạnh AC. Tính AD theo a để BD ⊥ AM.

Hướng dẫn giải:

Bài 4: Trong mặt phẳng tọa độ Oxy, cho hai vectơ 

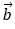
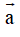
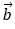
 = (3;m) và  = (1;7). Xác định m để góc giữa hai vectơ  và  là 45°.

Hướng dẫn giải:

Bài 5: Trong mặt phẳng tọa độ Oxy, cho hai vectơ 

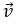
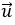
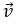
 = (-1;1) và  = (m;⁡2). Tìm m để góc giữa hai vectơ  và  là 135°.

Hướng dẫn giải:

Vậy không tồn tại m để góc giữa hai vectơ 

 và 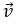 là 135°.

Bài 6: Trong mặt phẳng tọa độ Oxy cho hai vectơ 

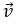
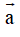
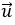
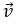
 = (4;1) và vectơ  = (1;4). Tìm m để vectơ =m. +  tạo với vectơ  một góc 45°.

Hướng dẫn giải:

Đáp án C

Bài 7: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài các đường trung tuyến của tam giác ABC.

Hướng dẫn giải:

Gọi độ dài trung tuyến từ các đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc.

Áp dụng công thức trung tuyến ta có:

Vì độ dài các đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:

Bài 8: Cho tam giác ABC, có BC = a, CA = b và AB = c. Chứng minh rằng nếu b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau.

Hướng dẫn giải:

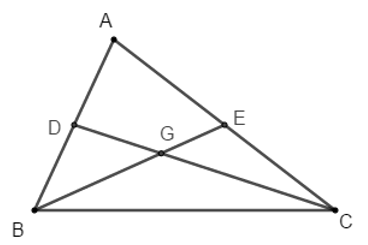
Gọi D và E lần lượt là trung điểm của AB và AC, G là trọng tâm tam giác ABC.

Đặt BE = mb, CD = mc

Áp dụng công thức trung tuyến trong tam giác ABC ta có:

Vậy b2 + c2 = 5a2 thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau. (đpcm)

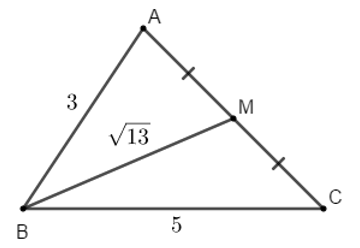
Bài 9: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến 

. Độ dài AC là:

Hướng dẫn giải:

BM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có:

Đáp án B

5. Bài tập trắc nghiệm:

Phần 1:

Câu 1: Cho hình vuông ABCD cạnh a. Khi đó,  bằng:

Câu 2: Cho hai điểm A = (1;2) và B = (3;4). Giá trị của AB là:

Câu 3: Cho tam giác ABC. Hãy tính 

Câu 4: Cho tam giác ABC có . Tính 

A. 20

B. 44

C. 64

D. 60

Câu 5: Tích vô hướng của hai vécto  cùng khác 0 là số âm khi:

A.  cùng chiều.

B.  cùng phương.

C. 

D.

Câu 6: Cho đoạn thẳng AB và điểm I là trung điểm của đoạn thẳng AB. M là một điểm bất kì. Hệ thức nào đây là đúng?

Câu 7: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Biểu thức: bằng:

Câu 8: Cho A(-6 ; 10), B(12 ; 2) . Tính AB.

Câu 9: Cho các vécto . Tích vô hướng của  là:

Câu 10: Trong mặt phằng Oxy, cho . Tính  ta được kết quả đúng là:

Câu 11: Cho tam giác ABC. Hãy tính 

Câu 12: Điều kiện của  và  sao cho  là:

 đối nhau.

 ngược hướng.

 bằng nhau.

 cùng hướng.

Câu 13: Cho tam giác đều ABC có cạnh bằng m. Khi đó  bằng:

Câu 14: Trong măt phẳng toạ độ Oxy cho ba điểm A(3; -1), B(2; 10), C(4; -2). Tích vô hướng  bằng bao nhiêu?

Câu 15: Trong mặt phẳng toạ độ Oxy cho hai điểm A(3; -1), B(2; 10). Tích vô hướng  bằng bao nhiêu?

Câu 16: Trong măt phẳng toạ độ Oxy cho ba điểm A(3; -1), B(2; 10), C(4; -2). Tích vô hướng  bằng bao nhiêu?

B. -12

Câu 17: Góc giữa hai vécto  là

Câu 18: Tam giác ABC vuông ở A và có góc . Hệ thức nào sau đây là sai?

Câu 19: Cho hai vécto . Góc giũa hai vécto  là

A. 90

B. 60

C. 45

D. 30

Câu 20: Trọng tâm G của tam giác ABC với A(-4; 7), B (2; 5), C(-1;-3) có tọa độ là:

A. (-1 ; 4)

B. (2 ; 6)

C. (-1 ; 2)

D. (-1 ; 3)

Đáp án phần trắc nghiệm

1- C	2- C	3-A	4- A	5- D
6- D	7- B	8- B	9- A	10- B
11- C	12- D	13-D	14-B	15- A
16- B	17- C	18- D	19- C	20- D

Phần 2:

Câu 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; -2), B (2; 1; -1). Độ dài của đoạn thẳng AB là

Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ 

 và 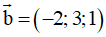. Khẳng định nào sau đây là sai?

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ

. Tính .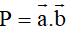

A. P = -10 

B. P = -40

C. P = 16

D. P = -34

Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ 

. Tính.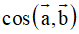

Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho 

. Khi đó 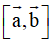 có tọa độ bằng

A. (0 ; 0 ; 0).

B. (1 ; 1 ; 1).

C. (2 ; 8 ; 2).

D. (1 ; -2 ; 1).

Câu 6: Cho bốn véc tơ 

Chọn mệnh đề đúng.

Câu 7: Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A (1; 1; 1), B (4; 3; 2), C (5; 2; 1). Diện tích tam giác ABC là

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có A (1; 0; 1), B (2; 0; -1), C (0; 1; 3), D (3; 1; 1). Thể tích khối tứ diện ABCD là

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD. A’B’C’D’ có A (-1; 0; 2), B (1; 1; -1), D (0; 1; 1), A’ (2; -1; 0). Thể tích V của khối hình hộp ABCD. A’B’C’D’ là

A. V = 1.                   

B. V = 4.                   

C. V = 5.                   

D. V = 6.

Câu 10: Cho ba vectơ

. Chọn mệnh đề đúng:

A. Ba vectơ đồng phẳng.

B. Ba vectơ không đồng phẳng.

C. Ba vectơ cùng phương.

D.

.

Đáp án:

Câu	1	2	3	4	5	6	7	8	9	10
Đáp án	D	B	A	B	A	C	D	A	C	A