Góc đồng vị là gì? Góc duy nhất trong? Góc cùng cạnh – định nghĩa và tính chất? Các dạng bài tập thường gặp? Phương pháp giải bài tập về góc và ví dụ minh họa?
1. Thế nào là góc đồng vị?
1.1. Định nghĩa và tính chất của hai góc đồng vị:
Trong hình học, một góc là một đối tượng hình học được xác định bởi hai tia có một điểm cuối chung. Hai tia này được gọi là tâm của góc và điểm cuối chung của chúng được gọi là đỉnh của nó. Các góc này được xác định nằm trên mặt phẳng Euclide, tuy nhiên một số góc cũng có thể được phân biệt trong hình học Euclide.
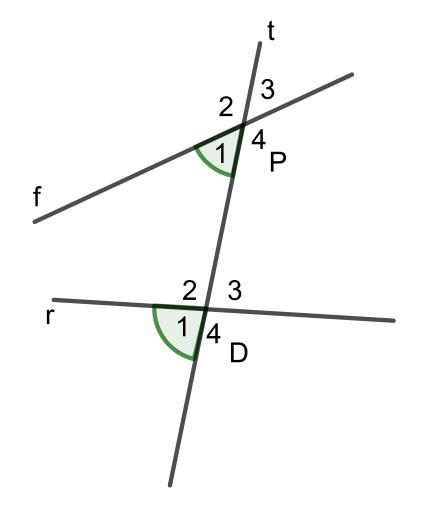
Nếu đường thẳng t cắt hai đường thẳng f và r mà trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc đồng vị còn lại cũng bằng nhau.
Hai góc PĐầu tiên và dễ dàngĐầu tiên được gọi là các góc đồng vị
Ta có thể hiểu hai góc đồng vị là hai góc nằm ở cùng một vị trí.
Có thể rút ra những dấu hiệu cơ bản để nhận biết mối quan hệ góc này là:
– Hai góc không chung gốc.
– Hai góc ở cùng một phía đối với đường thẳng cắt nhau và ở cùng một vị trí trên hai đường thẳng song song.
Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc trong so le trong thì:
– Hai góc so le trong còn lại bằng nhau
– Hai góc đồng vị thì bằng nhau
1.2. Phương pháp xác định hai góc đồng vị:
Để nhận biết hai góc đồng vị ta dựa vào các dấu hiệu sau:
Cho đường thẳng A cắt hai đường thẳng B và C tạo thành các góc. Khi đó các cặp góc đồng vị có đặc điểm:
đầu tiên, Hai góc không thể trùng gốc
Thứ hai, Hai góc đó phải cùng phía đối với đường thẳng A và ở cùng một vị trí trên hai đường thẳng B và C .
1.3. Các dạng bài tập về góc đồng vị:
Bài tập loại 1: Xác định hai góc đồng vị. Phương pháp giải dạng bài tập này dựa vào định nghĩa góc đồng vị.
Bài tập loại 2: Tính số đo góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Phương pháp giải của dạng bài tập này là vận dụng tính chất của góc đồng vị (hai góc đồng vị thì bằng nhau) để tìm hướng tính toán hợp lý.
Dạng bài tập 3: Chứng minh hai đường thẳng song song. Dựa vào định lí đảo góc đồng vị, nếu một đường thẳng cắt hai đường thẳng bất kỳ và hai góc đó trùng nhau một vị trí đồng vị thì hai đường thẳng đó song song.
2. Góc so le trong là gì?
2.1. Góc so le trong là gì?
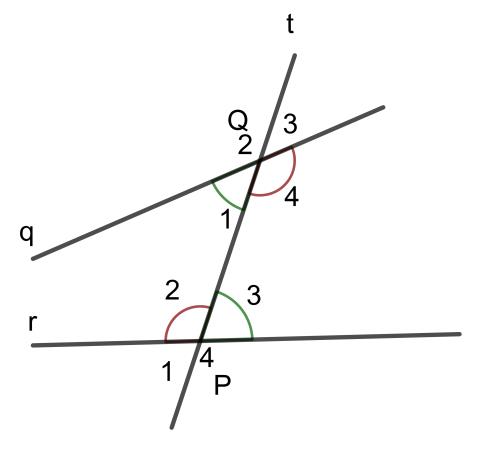
Định nghĩa các góc so le trong: Giả sử có một đường thẳng t cắt đường thẳng q tạo thành bốn góc và cắt đường thẳng r tạo thành bốn góc. Khi đó hai góc so le trong là hai góc không chung đỉnh, nằm bên trong hai đường thẳng q, r và nằm phía đối diện của đường thẳng t.
Ví dụ:
Q. gócĐầu tiên và góc P3 là hai góc so le trong
Tương tự, góc Q4 và góc P2 là hai góc so le trong
2.2 Thiên nhiên:
Nếu đường thẳng cc cắt hai đường thẳng aa và bb mà trong hai góc tạo thành có một cặp góc so le trong thì:
a) Hai góc so le trong còn lại thì bằng nhau.
b) Hai góc đồng vị (trong từng cặp) bằng nhau.
c) Hai góc trong cùng phía thì phụ nhau
Như sau:
Từ hình trên, ta thấy các góc Q3Hỏi4PĐầu tiênP2 là các góc trong của hai đường thẳng u và v.
Q. gócĐầu tiên và P3 là hai góc không có gốc chung gốc, nằm ở phía đối của đường thẳng t nên góc PĐầu tiên và T3 là hai góc so le trong.
Tương tự ta có góc Q4 và P2 là hai góc không có gốc chung gốc, nằm ở phía đối diện của đường thẳng t nên góc Q4 và P2 là hai góc so le trong.
Và góc QĐầu tiên và P2Hỏi4 và P3 cũng là các cặp góc không có chung gốc nhưng nằm cùng phía với đường thẳng q nên các cặp góc đó không phải là góc so le trong.
2.3. Dấu hiệu nhận biết hai góc so le trong:
Cho đường thẳng t cắt hai đường thẳng q và r tạo thành các góc. Khi đó để nhận biết hai góc so le trong ta dựa vào các dấu hiệu sau:
Dấu hiệu 1: Hai góc không thể trùng gốc
Dấu hiệu 2: Hai góc đó phải nằm bên trong hai đường thẳng q và r.
Dấu hiệu 3: Hai góc đó phải so le nhau hay nói cách khác hai góc đó phải nằm về phía đối của đường thẳng t.
3. Thế nào là góc cùng cạnh?
3.1. Định nghĩa:
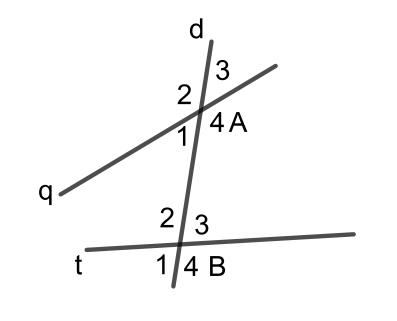
Giả sử có một đường thẳng d bất kỳ cắt hai đường thẳng q và t tạo thành các góc. Khi đó hai góc trong cùng phía là hai góc không đối đỉnh, nằm bên trong hai đường thẳng q và t và cùng phía với đường thẳng d.
Bình luận: Nếu đường thẳng d cắt hai đường thẳng q và t và q và t song song thì các góc trong cùng phía sẽ bù nhau. Khi đó tổng số đo của hai góc trong cùng phía sẽ bằng 180 .o.
Từ hình trên ta thấy góc AĐầu tiên và góc B2 là hai góc trong cùng phía.
Tương tự ta cũng có góc A4 và nhưng3 là hai góc trong cùng phía.
3.2. Cách xác định góc trong cùng phía:
Giả sử có đường thẳng d cắt đường thẳng q tại B và cắt đường thẳng t tại F tạo thành các góc của đỉnh B và đỉnh F. Khi đó để biết hai góc nào là hai góc trong cùng phía ta dựa vào các đặc điểm sau:
– Hai góc đó không chung gốc. Đó là, một góc đỉnh B và một góc đỉnh F.
– Hai góc đó đều nằm trong hai đường thẳng q và t.
– Hai góc đó cùng nằm về một phía của đường thẳng d. Nói cách khác, hai góc đó phải cùng phía với đường thẳng d.
4. Các dạng bài tập thường gặp:
– Dạng 1: Nhận biết các cặp góc trong so le trong, các cặp góc đồng vị, các cặp góc trong cùng phía.
– Dạng 2: Tính số đo của một góc khi biết một trong bốn góc tạo bởi hai đường thẳng.
– Dạng 3: Tìm các cặp góc bằng nhau, các cặp góc kề bù.
– Dạng 4: Xác định vị trí của các góc.
– Dạng 5: Chứng minh vị trí của các góc.
– Dạng 6: Tìm các cặp góc thỏa mãn điều kiện cho trước.
– Dạng 7: Vận dụng vị trí góc vào các bài toán khác: tam giác, vuông, tròn.
5. Phương pháp giải bài tập về góc và ví dụ minh họa:
Để giải tốt bài toán tính số đo góc thì người học đầu tiên Phải có những kiến thức cơ bản sau về góc và các mối quan hệ của nó như sau:
* Trong tam giác:
Tổng ba góc trong bằng 180°.
+ Khi BBiết hai góc ta xác định được góc còn lại.
* Trong tam giác cân: Biết một góc ta xác định được hai góc còn lại.
* Trong tam giác vuông:
Biết một góc nhọn ta xác định được góc nhọn còn lại.
Nếu cạnh góc vuông bằng một nửa cạnh huyền thì góc đối diện với cạnh đó có số đo là 30°30°.
* Trong tam giác vuông cân: Mỗi góc nhọn có số đo là 45°45°.
* Trong tam giác đều: Mỗi góc có số đo là 60°.60°.
* Tia phân giác của một góc chia góc đó thành hai góc có số đo bằng nhau.
* Hai tia phân giác của hai góc bù nhau thì vuông góc với nhau.
* Hai góc bằng nhau.
* Tính chất của góc trong so le trong, đồng vị, trong của một đường thẳng cắt hai đường thẳng song song.
Trong thực tế để giải bài toán tính số đo góc ta thường coi các góc đó trong mối liên hệ với các góc trong các hình đặc biệt nêu trên hoặc coi các góc tương ứng là bằng nhau. .. Đã sau đó bạn sẽ nghĩ ra kết quả.
Ví dụ minh họa 1: Nếu hai đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc trong so le trong thì:
A. Hai góc trong cùng phía thì bằng nhau
B. Hai góc đồng vị thì bằng nhau
C. Hai góc so le trong còn lại có tổng bằng 120°
D. Tất cả các câu trả lời trên đều đúng
Câu trả lời nên chọn là: GET
Nếu đường thẳng c cắt hai đường thẳng a và trong các góc tạo thành có một cặp góc trong so le trong thì: hai góc đồng vị bằng nhau
Ví dụ minh họa #2: Nếu hai đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:
A. Hai góc trong cùng phía thì bằng nhau
B. Hai góc so le trong thì phụ nhau
C. Hai góc trong cùng phía thì phụ nhau
D. Tất cả các câu trả lời trên đều đúng
Đáp án nên chọn là:
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A, B và trong các góc tạo thành có một cặp góc đồng vị bằng nhau, giả sử
+ Xét một cặp góc trong cùng phía chẳng hạn
Do đó hai góc trong cùng phía phụ nhau nên A sai, C đúng
Vậy hai góc so le trong bằng nhau. Đáp án B sai