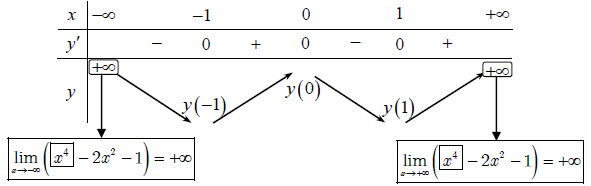1. Hàm số đồng biến khi nào, nghịch biến khi nào:
Ví dụ K là một khoảng, một đoạn hoặc một nữa khoảng và y = f(x) là một hàm số xác định trên K.
+ Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu: ∀ x1, x2 ∊ f (x1) < f (x2)
+ Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu: ∀ x1, x2 ∊ f (x1) > f (x2)
Hàm số đồng biến hoặc nghịch biến trên K
Nhận xét 1: Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên D thì hàm số f(x) + g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f(x) – g(x)
Nhận xét 2: Nếu hàm số f(x) và g(x) là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số f(x)․g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số f(x) và g(x) không là các hàm số dương trên D.
Nhận xét 3
Cho hàm số u = u(x) xác định với x ∊ (a;b) và u(x) ∊ (c;d). Hàm số f [u(x)] cũng xác định với x ∊ (a;b). Ta có nhận xét sau:
Giả sử hàm số u = u(x) đồng biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] đồng biến với x ∊ (a;b) ⇔ f(u) đồng biến với u(x) ∊ (c;d)
Giả sử hàm số u = u(x) nghịch biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] nghịch biến với x ∊ (a;b) ⇔ f(u) nghịch biến với u(x) ∊ (c;d)
-> Định lí 1
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
– Nếu hàm số đồng biến trên khoảng K thì f’(x) ≥ 0, ∀ x ∊ K
– Nếu hàm số nghịch biến trên khoảng K thì f’(x) ≤ 0, ∀ x ∊ K
-> Định lí 2.
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
– Nếu f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên K.
– Nếu f’(x) < 0, ∀ x ∊ K thì hàm số f nghịch biến trên K.
– Nếu f’(x) = 0, ∀ x ∊ K thì hàm số f không đổi trên K.
-> Định lí 3. (mở rộng của định lí 2)
Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:
– Nếu f’(x) ≥ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
– Nếu f’(x) ≤ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f nghịch biến trên K.
2. Cách xác định hàm số đồng biến, nghịch biến:
Muốn xác định hàm số đã cho là hàm số đồng biến hay hàm số nghịch biến sẽ thực hiện theo các bước sau:
– Bước 1: Tìm tập xác định
– Bước 2: Tính đạo hàm của hàm số đã cho
– Bước 3: Tìm các điểm khi f'(x) = 0 hoặc không xác định
– Bước 4: Lập bảng biến thiên, trong đó sắp xếp các điểm theo thứ tự tăng dần
– Bước 5: Từ bảng biến thiên rút ra kết luận về khoảng đồng biến, nghịch biến của hàm số đã cho
3. Dạng bài tập tính đồng biến nghịch biến của hàm số:
Dạng 1: Tìm khoảng đồng biến – nghịch biến của hàm số
Cho hàm số y = f(x)
+) f’(x) > 0 ở đâu thì hàm số đồng biến ở đấy.
+) f’(x) < 0 ở đâu thì hàm số nghịch biến ở đấy.
Quy tắc:
+) Tính f’(x), giải phương trình f’(x) = 0 tìm nghiệm.
+) Lập bảng xét dấu f’(x)
+) Dựa vào bảng xét dấu và kết luận.
Ví dụ 1. Cho hàm số f(x) đồng biến trên tập số thực ℝ, mệnh đề nào sau đây là đúng?
A. Với mọi x1 > x2 ∊ ℝ ⇒ f (x1) < f (x2)
B. Với mọi x1, x2 ∊ ℝ ⇒ f (x1) > f (x2)
C. Với mọi x1, x2 ∊ ℝ ⇒ f (x1) < f (x2)
D. Với mọi x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2)
-> Chọn đáp án D.
Ta có: f(x) đồng biến trên tập số thực ℝ.
⇒ x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2)
Ví dụ 2. Cho hàm số f(x) = -2×3 + 3×2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên ℝ
B. f (a) > f (b)
C. f (b) < 0
D. f (a) < f (b)
-> Chọn đáp án D.
Ta có: f’(x) = -6×2 + 6x – 3 < 0, ∀ x ∊ ℝ
⇒ Hàm số nghịch biến trên ℝ.
0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)
Dạng 2: Tìm điều kiện của tham số
Kiến thức chung
+) Để hàm số đồng biến trên khoảng (a;b) thì f’(x) ≥ 0, ∀ x ∊ (a;b).
+) Để hàm số nghịch biến trên khoảng (a;b) thì f’(x) ≤ 0, ∀ x ∊ (a;b).
*) Riêng hàm số:
. Có TXĐ là tập D. Điều kiện như sau:
+) Để hàm số đồng biến trên TXĐ thì y’ > 0, ∀ x ∊ D.
+) Để hàm số nghịch biến trên TXĐ thì y’ < 0, ∀ x ∊ D.
+) Để hàm số đồng biến trên khoảng (a;b) thì
+) Để hàm số nghịch biến trên khoảng (a;b) thì
*) Tìm m để hàm số bậc 3 y = ax3 + bx2 + cx + d đơn điệu trên ℝ
+) Tính y = 3ax2 + 2bx + c là tam thức bậc 2 có biệt thức ∆.
+) Để hàm số đồng biến trên ℝ
+) Để hàm số nghịch biến trên ℝ
Chú ý: Cho hàm số y = ax3 + bx2 + cx + d
+) Khi a > 0 để hàm số nghịch biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k
+) Khi a < 0 để hàm số đồng biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k
Ví dụ 1. Hàm số y = x3 – 3×2 + (m – 2) x + 1 luôn đồng biến khi:
A. m ≥ 5
B. m ≤ 5
C.
D.
-> Chọn đáp án A.
Ta có: y’ = 3×2 – 6x + m – 2
Hàm số đồng biến trên ℝ khi và chỉ khi y’ = 3×2 – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ
⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5
Ví dụ 2. Hàm số y = ⅓x3 – mx2 – (3m + 2) x + 1 đồng biến trên ℝ khi m bằng
A.
B.
C. -2 ≤ m ≤ -1
D. -2 < m < -1
-> Chọn đáp án C
Ta có: y’ = x2 – 2mx – 3m + 2
Hàm số đồng biến trên ℝ khi và chỉ khi y’ = x2 – 2mx – 3m + 2 ≥ 0, ∀ x ∊ ℝ
⇔ ∆’ ≤ 0 ⇔ m2 + 3m + 2 ≤ 0 ⇔ -2 ≤ m ≤ -1
Dạng 3: Xét tính đơn điêu hàm số trùng phương
Bước 1: Tìm tập xác định
Bước 2: Tính đạo hàm f’(x) = 0. Tìm các điểm xi (i= 1, 2,… n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ 1. Xét tính đơn điệu của mỗi hàm số sau: y = x4 – 2×2 + 1
Hàm số xác định với mọi x ∊ ℝ
y’ = 4×3 – 4x = 4x (x2 – 1)
Cho y’ = 0 ⇒ x = 0 hoặc x = -1 hoặc x = 1
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra:
- Hàm số đồng biến trên các khoảng (-1;0) và (1; +∞).
- Hàm số nghịch biến trên các khoảng (-∞; -1) và (0;1)
Ví dụ 2. Xét tính đơn điệu của mỗi hàm số sau: y = ¼x4 + 2×2 – 1
Hàm số xác định với mọi x ∊ ℝ
y’ = x3 + 4x = x (x2 + 4)
Cho y’ = 0 ⇒ x = 0 (do x2 + 4 = 0 vô nghiệm)
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra:
- Hàm số đồng biến trên khoảng (0; +∞)
- Hàm số nghịch biến trên khoảng (-∞; 0)