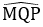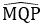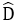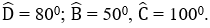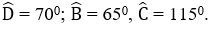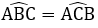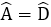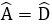Hình thang vuông là một loại hình thang đặc biệt, với một góc vuông tại một trong các đỉnh của nó. Trong hình thang vuông, các cạnh bên kề với góc vuông có độ dài bằng nhau, và đường chéo lớn (đường nối hai đỉnh không đối diện) là đường trung bình của hình thang.
1. Hình thang vuông là gì?
Hình thang vuông là một loại hình thang đặc biệt, với một góc vuông tại một trong các đỉnh của nó. Trong hình thang vuông, các cạnh bên kề với góc vuông có độ dài bằng nhau, và đường chéo lớn (đường nối hai đỉnh không đối diện) là đường
Hình thang vuông còn được gọi là hình bàn chân, vì hình dáng của nó giống như một chiếc bàn chân với gót chân là góc vuông. Hình thang vuông là một khái niệm quan trọng trong hình học, được sử dụng rất nhiều trong thực tế. Ví dụ, trong
Hình thang vuông cũng có ứng dụng trong giải các bài toán hình học, ví dụ như tính diện tích, chu vi, hay các đại lượng hình học khác của hình thang vuông. Nếu bạn là một học sinh học về hình học, hình thang vuông là một khái niệm cần thiết để bạn có thể hiểu và giải quyết các bài toán liên quan đến hình thang và hình học nói chung.
Vì vậy, nắm vững khái niệm về hình thang vuông và các tính chất của nó là rất quan trọng, và có thể giúp bạn cải thiện kỹ năng giải toán hình học của mình.
2. Đặc điểm tính chất hình thang vuông:
Hình thang vuông là một dạng hình học đặc biệt, được sử dụng phổ biến trong nhiều bài toán hình học và các lĩnh vực khác nhau.
2.1. Tính chất chung:
Hình thang vuông có những đặc điểm chung sau:
– Hình thang vuông có hai cạnh đáy song song với nhau và vuông góc với hai đáy, tạo nên một góc vuông ở đáy. Điều này có nghĩa là cả hai đường chéo của hình thang vuông đều là các đường chéo vuông góc với nhau.
– Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy cũng bằng nhau. Điều này có nghĩa là một hình thang có thể có các cạnh đáy và bên bằng nhau. Khi đó, hình thang đó sẽ là một hình thang cân.
– Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau. Điều này có nghĩa là một hình thang có thể có các cạnh bên và đáy bằng nhau. Khi đó, hình thang đó sẽ là một hình thang đều.
2.2. Tính chất đặc biệt:
Ngoài những đặc điểm chung trên, hình thang vuông còn có một số tính chất đặc biệt khác như:
– Tính chất đối xứng: Hình thang vuông là một hình chữ nhật bị cắt một phần bởi một đường chéo. Do đó, hình thang vuông có tính chất đối xứng qua đường chéo.
– Tính chất tiêu biểu: Hình thang vuông là một dạng hình học rất tiêu biểu, có thể được sử dụng để giải quyết các bài toán liên quan đến diện tích, chu vi, và khoảng cách giữa các đường thẳng.
– Tính chất ứng dụng: Hình thang vuông là một hình dạng phổ biến trong các bài toán về diện tích và chu vi, và cũng có thể được sử dụng để giải quyết các bài toán liên quan đến thể tích và khối lượng.
– Tính chất tương tự: Hình thang vuông có thể được coi là một dạng biến thể của hình thang và hình chữ nhật, vì nó kết hợp những đặc điểm chung của hai hình học này. Do đó, tính chất tương tự của hình thang vuông cũng được áp dụng cho các hình học tương tự khác.
Tóm lại, hình thang vuông là một hình học đặc biệt với nhiều đặc điểm và tính chất đặc trưng, có thể được sử dụng để giải quyết nhiều bài toán hình học và các lĩnh vực khác nhau. Việc hiểu rõ về tính chất của hình thang vuông sẽ giúp cho việc giải quyết các bài toán liên quan đến hình học trở nên dễ dàng hơn.
3. Dấu hiệu nhận biết hình thang vuông:
Ngoài việc hình thang vuông có một góc vuông, còn có những đặc điểm khác để phân biệt với các loại hình thang khác. Ví dụ, hình thang vuông có hai đường chéo bằng nhau và vuông góc với nhau, các cạnh đối diện của nó bằng nhau và song song với nhau. Ngoài ra, hình thang vuông còn có thể được phân loại là hình vuông nếu cả bốn cạnh của nó bằng nhau và cả bốn góc của nó đều là vuông.
Vì vậy, khi xác định một hình thang là hình thang vuông, chúng ta cần xem xét các đặc điểm trên để đảm bảo rằng nó thỏa mãn tất cả các tiêu chí của hình thang vuông. Điều này có thể giúp chúng ta phân biệt các loại hình thang với nhau và giúp chúng ta hiểu rõ hơn về tính chất của chúng.
4. Bài tập vận dụng:
Bài 1: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.
Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
Đáp án cần chọn là: C
Bài 2: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E. Chọn khẳng định đúng nhất?
A. Tứ giác BDIC là hình thang
B. Tứ giác BIEC là hình thang
C. Tứ giác BDEC là hình thang
D. Cả A, B, C đều đúng
Đáp án cần chọn là: D
Bài 3: Cho hình thang cân MNPQ (MN // PQ) có góc
= 450 và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
A. 728 cm2
B. 346 cm2
C. 364 cm2
D. 362 cm2
Đáp án cần chọn là: C
Bài 4: Cho hình thang cân MNPQ (MN // PQ) có góc
= 450 và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
A. 418 cm2
B. 209 cm2
C. 290 cm2
D. 580 cm2
Đáp án cần chọn là: B
Bài 5: Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và
= 450. Độ dài đáy lớn CD bằng
A. 12cm
B. 16 cm
C. 18 cm
D. 20 cm
Đáp án cần chọn là: B
Bài 6: Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và
= 450. Độ dài đáy lớn CD bằng
A. 13 cm
B. 10 cm
C. 12 cm
D. 8 cm
Đáp án cần chọn là: A
Bài 7: Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
A. 4,5 cm
B. 4 cm
C. 3,5 cm
D. 3 cm
Đáp án cần chọn là: B
Bài 8: Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
A. 9 cm
B. 8 cm
C. 12 cm
D. 6 cm
Đáp án cần chọn là: C
Bài 9: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
A. Hình thang
B. Hình thang cân
C. Hình thang vuông
D. Cả A, B, C đều sai
Đáp án cần chọn là: B
Bài 10: Hãy chọn câu sai.
A. Hình thang là tứ giác có hai cạnh đối song song.
B. Nếu hình thanh có hai cạnh bên song song thì tất cả các cạnh của hình thang bằng nhau.
C. Nếu một hình thang có hai cạnh đáy bằng nhau thị hai cạnh bên bằng nhau, hai cạnh bên song song.
D. Hình thang vuông là hình thang có một góc vuông.
Đáp án cần chọn là: B
Bài 11: Câu nào sau đây là đúng khi nói về hình thang:
A. Hình thang là tứ giác có hai cạnh đối song song.
B. Hình thang là tứ giác có hai cạnh đối bằng nhau
C. Hình thang là tứ giác có hai cạnh kề bằng nhau
D. Cả A, B, C đều sai
Đáp án cần chọn là: A
Bài 12: Chọn câu đúng nhất.
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau
D. Cả A, B, C đều đúng
Đáp án cần chọn là: D
Bài 13: Hình thang ABCD có
Số đo góc  là:
A. 1300
B. 1400
C. 700
D. 1200
Đáp án cần chọn là: A
Bài 14: Hình thang ABCD có
Số đo góc  là:
A. 1300
B. 1400
C. 700
D. 1100
Đáp án cần chọn là: D
Bài 15: Góc kề cạnh bên của hình thang có số đo là 700. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 1200
C. 1100
D. 1800
Đáp án cần chọn là: C
Bài 16: Góc kề cạnh bên của hình thang có số đo là 1300. Góc kề còn lại của cạnh bên đó là:
A. 700
B. 1000
C. 400
D. 500
Đáp án cần chọn là: D
Bài 17: Cho tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chọn khẳng định đúng
A. ABCD là hình thang
B. ABCD là hình thang vuông
C. ABCD là hình thang cân
D. Cả A, B, C đều sai
Đáp án cần chọn là: A
Bài 18: Cho tam giác ΔAMN cân tại A. Các điểm B, C lần lượt trên các cạnh AM, AN sao cho AB = AC. Hãy chọn câu đúng:
A. MB = NC
B. BCNM là hình thang cân
C.
D. Cả A, B, C đều đúng
Đáp án cần chọn là: D
Bài 19: Cho hình thang vuông ABCD có
= 900, AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
A. 1370
B. 1360
C. 360
D. 1350
Đáp án cần chọn là: D
Bài 20: Cho hình thang ABCD có
= 900, DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
A. 1100
B. 1500
C. 1200
D. 1350
Đáp án cần chọn là: C
Bài 21: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE.
Tứ giác BDEC là hình gì?
A. Hình thang
B. Hình thang vuông
C. Hình thang cân
D. Cả A, B, C đều sai
Đáp án cần chọn là: C