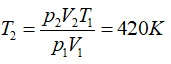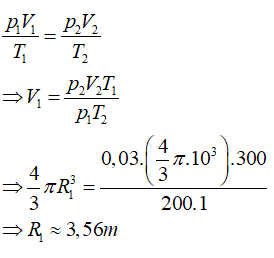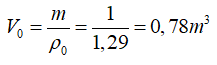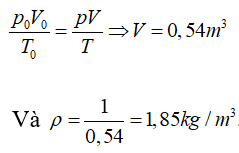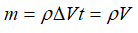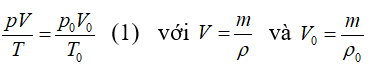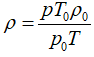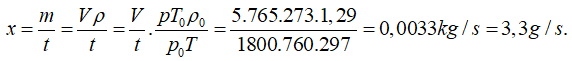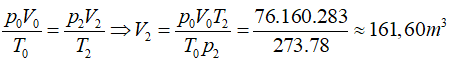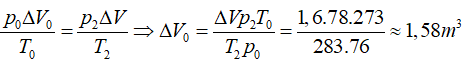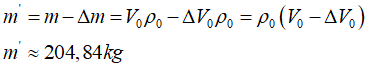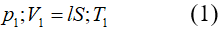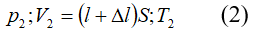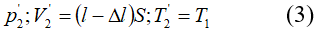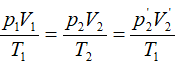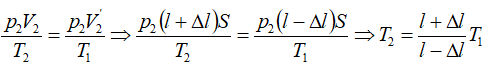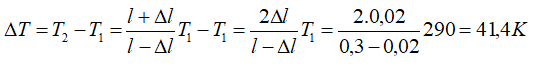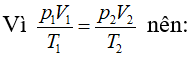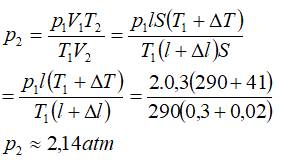Khí lý tưởng là gì? Lập phương trình trạng thái khí lý tưởng?

Bạn đang xem: Khí lý tưởng là gì? Lập phương trình trạng thái khí lý tưởng? tại truongptdtntthptdienbiendong.edu.vn

Các loại khí lý tưởng đóng vai trò quan trọng trong việc hiểu sâu hơn về tính chất của khí và hệ thống hạt trong lý thuyết vật lý. Dưới đây là bài viết về chủ đề: Khí lý tưởng là gì? Lập phương trình trạng thái khí lý tưởng?, mời bạn đọc theo dõi.

1. Khí lý tưởng là gì?

1.1. Khái niệm:

Khí lý tưởng là một khái niệm trong vật lý và hóa học để mô tả một loại chất được giả định tuân theo một số quy tắc và đặc điểm cụ thể. Mô hình khí lý tưởng giúp đơn giản hóa việc nghiên cứu và hiểu các tính chất của các loại khí trong điều kiện nhất định.

Khi khí thực ở trong điều kiện áp suất cao và nhiệt độ thấp, như ở gần các điểm đặc biệt như điểm sôi hoặc điểm đông, các hiệu ứng tương tác giữa các phân tử khí sẽ bắt đầu trở nên đáng kể. Trong các điều kiện này, kích thước của các phân tử, cùng với tương tác không chỉ là va chạm đàn hồi, sẽ tạo ra sự khác biệt so với mô hình khí lý tưởng. Điều này thường dẫn đến việc sử dụng các phương trình trạng thái khác như phương trình Van der Waals để xác định các tính chất khí thực một cách chính xác hơn trong các điều kiện đặc biệt.

1.2. Đặc điểm:

Dưới đây là một số đặc điểm quan trọng của khí lý tưởng:

– Phân tử không gian: Trong khí lý tưởng, các phân tử của khí được giả định không tương tác lẫn nhau, tức là không có tương tác giữa chúng.

– Thể tích phân tử: Phân tử của khí lý tưởng được coi là không có thể tích, tức là chúng rất nhỏ so với thể tích chứa khí.

– Tương tác phân tử và tường thành: Các phân tử trong khí lý tưởng không tương tác với tường thành hoặc bất kỳ vật thể nào khác xung quanh. Sự va chạm giữa các phân tử được xem xét theo mô hình va chạm hoàn toàn đàn hồi.

– Năng lượng nhiệt động: Khí lý tưởng có năng lượng nhiệt động cao, và năng lượng này chủ yếu được chuyển đổi thành chuyển động ngẫu nhiên của các phân tử.

– Chuyển đổi pha: Trong mô hình khí lý tưởng, không có sự thay đổi pha (chuyển từ khí sang lỏng hoặc rắn) khi tăng áp suất hoặc giảm nhiệt độ. Chuyển đổi pha diễn ra ở nhiệt độ và áp suất nhất định được gọi là điểm sôi và điểm đông của chất.

Cần lưu ý rằng, mô hình khí lý tưởng là một mô hình đơn giản và thường chỉ áp dụng trong điều kiện ở áp suất thấp và nhiệt độ cao. Khi áp suất cao và nhiệt độ thấp hơn, các hiệu ứng tương tác giữa các phân tử sẽ trở nên quan trọng và mô hình khí lý tưởng không còn áp dụng.

2. Các loại khí lý tưởng:

Các loại khí lý tưởng đóng vai trò quan trọng trong việc hiểu sâu hơn về tính chất của khí và hệ thống hạt trong lý thuyết vật lý. Khái niệm về khí lý tưởng không chỉ đơn thuần là một mô hình đơn giản để mô tả hành vi của các phân tử khí mà còn là nền tảng để nghiên cứu sự biến đổi và cấu trúc của vật chất.

Loại đầu tiên là khí lý tưởng cổ điển, đây là một mô hình cơ bản trong lý thuyết khí. Mô hình này dựa trên giả thiết rằng các phân tử khí không tương tác mạnh với nhau và có thể coi như không có kích thước. Tính chất chính của khí lý tưởng cổ điển được mô tả bởi phân phối thống kê Maxwell-Boltzmann, trong đó xác suất tìm thấy các phân tử ở một tốc độ cụ thể được biểu thị bởi phân phối Gaussian. Mô hình này không xem xét các hiệu ứng lượng tử và thường chỉ áp dụng ở nhiệt độ cao.

Loại thứ hai là khí lý tưởng lượng tử tuân thủ thống kê Bose. Điều đặc biệt ở loại này là các phân tử giống nhau có thể tồn tại ở cùng một trạng thái. Điều này dẫn đến sự hiện tượng kỳ diệu được gọi là “sự thống nhất của Bose-Einstein”, nơi một số lượng lớn các hạt có thể tồn tại trong cùng một trạng thái năng lượng. Điều này thường được quan sát ở nhiệt độ thấp gần với không động năng tối thiểu.

Khí lý tưởng lượng tử tuân thủ thống kê Fermi là loại thứ ba, nơi ngược lại với loại Bose, các hạt không thể tồn tại trong cùng một trạng thái năng lượng. Đây là nguyên tắc cơ bản đằng sau nguyên tắc loại trừ Pauli, một nguyên tắc quan trọng trong cấu trúc điện tử của các nguyên tử và phân tử. Khí lý tưởng Fermi thường liên quan đến các hệ thống chứa các hạt baryon, chẳng hạn như các nguyên tử trong vật liệu.

Trong thực tế, khí lý tưởng cổ điển có thể được phân chia thành hai loại khác nhau dựa trên tính chất của chúng. Loại thứ nhất, thuần túy cổ điển, cho phép một hằng số vô định được cộng vào entropy. Điều này phản ánh sự không rõ ràng trong việc định rõ tất cả các trạng thái năng lượng của các phân tử khí. Loại thứ hai là giới hạn của hai loại khí lý tưởng lượng tử ở nhiệt độ cao. Trong trường hợp này, hằng số cộng thêm vào entropy được xác định cụ thể, giúp chúng ta hiểu rõ hơn về sự biến đổi của các hệ thống khí ở nhiệt độ cao và tạo điều kiện cho sự chuyển đổi từ hệ thống lượng tử sang hệ thống cổ điển khi nhiệt độ tăng lên.

3. Lập phương trình trạng thái khí lý tưởng:

Phương trình trạng thái của khí lý tưởng là một công cụ quan trọng trong lĩnh vực vật lý và hóa học, cho phép mô tả mối liên hệ giữa áp suất, thể tích và nhiệt độ của một loại khí lý tưởng đang ở trong trạng thái cân bằng nhiệt động. Đây là một khái niệm rất hữu ích để hiểu và dự đoán hành vi của các loại khí trong nhiều điều kiện khác nhau, mặc dù vẫn tồn tại một số giới hạn trong việc áp dụng phương trình này.

Phương trình trạng thái khí lý tưởng được công thức hóa dưới dạng $P V = n RT$ , trong đó:

$P$ là áp suất của khí.
$V$ là thể tích của khí.
$n$ là số mol của khí.
$R$ là hằng số khí lý tưởng.
$T$ là nhiệt độ tuyệt đối của khí.

Phương trình này đã được sáng tạo ra bởi nhà vật lý Benoit Clapeyron vào năm 1834. Ông đã kết hợp các định luật Boyle, Charles và Avogadro để tạo ra phương trình mô tả mối liên hệ giữa các đại lượng này.

Trong hệ đo lường quốc tế, đơn vị áp suất là pascal (Pa), đơn vị thể tích là mét khối (m³), và đơn vị nhiệt độ là kelvin (K). Hằng số khí lý tưởng $R$ trong trường hợp này có giá trị xấp xỉ

Tuy nhiên, trong một số hệ đo lường khác, người ta thường sử dụng giá trị khác cho hằng số $R$ , ví dụ như

khi đơn vị áp suất là atm và đơn vị thể tích là lít.

Cần nhấn mạnh rằng phương trình trạng thái khí lý tưởng chỉ là một mô hình đơn giản và thường chỉ đúng đối với các khí ở trạng thái gần với khí lý tưởng, đặc biệt là các khí đơn nguyên tử, ở nhiệt độ cao và áp suất thấp. Phương trình này bỏ qua kích thước thực tế của các phân tử khí so với thể tích toàn bộ của khí và không xem xét tương tác giữa các phân tử ngoại trừ tương tác va chạm đàn hồi ở khoảng cách rất nhỏ. Đối với các khí có hiệu ứng tương tác lớn hơn, các phương trình trạng thái khác như phương trình Van der Waals sẽ cần được áp dụng để tính toán chính xác hơn.

4. Bài tập về phương trình trạng thái khí lý tưởng:

Bài 1: Một lượng khí đựng trong một xi lanh có pittông chuyển động được. Các thông số trạng thái của lượng khí này là: 2 atm, 300K. Khi pit tong nén khí, áp suất của khí tăng lên tới 3,5 atm, thể tích giảm còn 12l. Xác định nhiệt độ của khí nén.

Lời giải:

Bài 2: Một bóng thám không được chế tạo để có thể tăng bán kính lên tới 10m khi bay ở tầng khí quyển có áp suất 0,03atm và nhiệt độ 200K. Hỏi bán kímh của bóng khi bơm, biêt bóng được bơm khí ở áp suất 1 atm và nhiệt độ 300K ?

Lời giải:

Bài 3: Tính khối lượng riêng của không khí ở nhiệt độ 100°C và áp suất 2.10⁵Pa. Biết khối lượng riêng của không khí ở 0°C và 1,01.10⁵ Pa là 1,29kg/m³.

Lời giải:

Thể tích của 1 kg không khí ở điều kiện chuẩn là:

Ở 0°C và 101 kPa: p_o = 101 kPa

V₀ = 0,78 m³

T₀ = 273 K

Ở 100°C và 200 kPa: p = 200 kPa

T = 373 K

V = ?

Ta có:

Bài 4: Một bình cầu dung dịch 20l chứa oxi ở nhiệt độ 16°C và áp suất 100atm. Tính thể tích của lượng khí này ở điều kiện chuẩn. Tạo sao kết quả tìm được chỉ là gần đúng?

Lời giải:

V₀ = 1889 lít.

Vì áp suất quá lớn nên khí không thể coi là khí lí tưởng. Do đó kết quả tìm được chỉ mang tính gần đúng

Bài 5: Người ta bơm khí oxi ở điều kiện chuẩn vào một bình có thể tích 5000l. sau nữa giờ bình chứa đầy khí ở nhiệt độ 24°C và áp suất 765mmHg. Xác định khối lượng khí bơm vào sau mỗi giây. Coi quá trình bơm diễn ra một cách điều đặn.

Lời giải:

Lượng khí bơm vào trong mỗi giây: 3,3g.

Sau t giây khối lượng khí trong bình là:

Với ρ là khối lượng riêng của khí.

ΔV là thể tích khí bơm vào sau mỗi giây.

V là thể tích khí bơm vào sau t giây.

thay V và V₀ vào (1) ta được: Vật Lí lớp 10 | Chuyên đề: Lý thuyết và Bài tập Vật Lí 10 có đáp án

Lượng khí bơm vào sau mỗi giây là:

Bài 6: Một phòng có kích thước 8m x 5m x 4m. Ban đầu không khí trong phòng ở điều kiện chuẩn, sau đó nhiệt độ của không khí tăng lên tới 10°C, trong khi áp suất là 78 cmHg. Tính thể tích của lượng khí đã ra khỏi phòng và khối lượng không khí còn lại trong phòng.

Lời giải:

ΔV = 1,6m³ ; m’ = 204,84 kg

Lượng không khí trong phòng ở trạng thái ban đầu (điều kiện chuẩn)

p₀ = 76 cmHg ; V₀ = 5.8.4 = 160 m³ ; T₀ = 273 K

Lượng không khí trong phòng ở trạng thái 2:

p₂ = 78 cmHg ; V₂ ; T₂ = 283 K

Ta có:

Thể tích không khí thoát ra khỏi phòng:

ΔV =V₂ – V₀ = 161,6 – 160 = 1,6 m³

Thể tích không khí thoát ra khỏi phòng tính ở điều kiện chuẩn là:

Khối lượng không khí còn lại trong phòng:

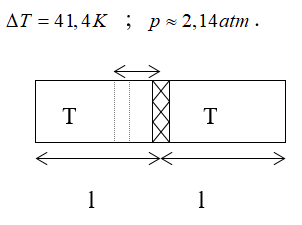
Bài 7: Một xi lanh có pittong cách nhiệt và nằm ngang. Pittong ở vị trí chia xi lanh thành hai phần bằng nhau, chiều dài của mỗi phần là 30cm. Mỗi phần chứa một lượng khí như nhau ở nhiệt độ 17°C và áp suất 2 atm. Muốn pittong dịch chuyển 2cm thì phải đun nóng khí ở một phần lên thêm bao nhiêu ? Áp suất cuả khí pittong đã dịch chuyển là bao nhiêu.

Lời giải: