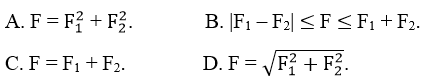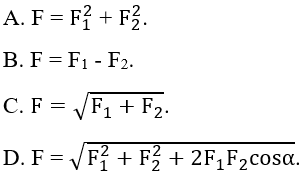Điều kiện cân bằng của một chất điểm là một khái niệm cơ bản trong vật lý và được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu rõ về khái niệm này sẽ giúp chúng ta giải quyết nhiều vấn đề trong cuộc sống và trong học tập, nghiên cứu. Vì vậy, trong bài viết dưới đây chúng tôi sẽ giới thiệu cho bạn đọc những nội dung cơ bản của phân tích lực và điều kiện cân bằng chất điểm.
1. Phân tích lực:
1.1. Phân tích lực là gì?
Phân tích lực là một phương pháp phân tích tác động của hai hoặc nhiều lực đối với một cơ thể. Cách áp dụng phương pháp này là thay thế một lực duy nhất bằng hai hoặc nhiều lực khác có tác dụng giống hệt như lực ban đầu.
1.2. Ứng dụng:
Phân tích lực là một công cụ quan trọng trong lĩnh vực vật lý, kỹ thuật, cơ học và địa chất học. Việc hiểu rõ về phương pháp phân tích lực giúp chúng ta hiểu rõ hơn về cách các lực tác động lên một cơ thể và có thể tách chúng thành các lực khác nhau để dễ dàng đánh giá tác động của từng lực đối với cơ thể.
Các ứng dụng của phân tích lực rất đa dạng. Trong lĩnh vực xây dựng, phân tích lực giúp các kỹ sư đánh giá tải trọng tác động lên các bộ phận của một công trình, từ đó đưa ra những
1.3. Cách áp dụng:
Để áp dụng phương pháp phân tích lực, chúng ta cần biết một lực có thể tác động theo hai hoặc nhiều hướng khác nhau. Nhờ đó, ta có thể tách một lực thành nhiều lực khác nhau và đưa ra những dự đoán chính xác hơn về tác động của chúng đối với cơ thể.
Việc hiểu rõ về phân tích lực cũng giúp chúng ta hiểu rõ hơn về cơ chế hoạt động của các thiết bị, từ đó giúp chúng ta đưa ra những giải pháp tối ưu hóa hiệu suất và độ ổn định của các thiết bị. Ngoài ra, phương pháp phân tích lực cũng giúp chúng ta hiểu rõ hơn về cơ chế hoạt động của các thiết bị, đồng thời giúp chúng ta đưa ra những giải pháp tối ưu hóa hiệu suất và độ ổn định của các thiết bị.
Tóm lại, phân tích lực là một công cụ quan trọng trong việc đánh giá tải trọng và tính ổn định của các công trình, thiết bị và máy móc. Việc áp dụng phương pháp phân tích lực đòi hỏi sự am hiểu sâu sắc về các lực tác động lên một cơ thể, cũng như sự hiểu biết về cơ chế hoạt động của các thiết bị. Tuy nhiên, nếu được áp dụng đúng cách, phương pháp này có thể giúp chúng ta đưa ra những quyết định quan trọng trong việc thiết kế và xây dựng các công trình và thiết bị.
2. Điều kiện cân bằng của chất điểm:
Điều kiện cân bằng của một chất điểm là một khái niệm cơ bản trong vật lý và được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu rõ về khái niệm này sẽ giúp chúng ta giải quyết nhiều vấn đề trong cuộc sống và trong học tập, nghiên cứu.
Thật vậy, khi một chất điểm đứng yên cân bằng, thì tổng hợp các lực đang tác dụng lên nó phải bằng không. Điều này có nghĩa là các lực đang tác động lên chất điểm phải hoàn toàn cân bằng lẫn nhau, không có lực nào chiếm ưu thế hơn lực khác.
Các lực tác động lên chất điểm có thể bao gồm lực đàn hồi, lực ma sát, lực hấp dẫn, lực điện và nhiều loại lực khác. Tuy nhiên, trong trường hợp chất điểm đang đứng yên cân bằng, tổng hợp tất cả các lực này phải bằng không.
Để hiểu rõ hơn về điều kiện cân bằng của chất điểm, chúng ta có thể áp dụng định luật Newton thứ ba. Theo định luật này, mỗi lực tác động lên một chất điểm sẽ đều tạo ra một phản lực tương ứng. Vì vậy, nếu một chất điểm đứng yên cân bằng, tổng hợp tất cả các lực tác động lên nó phải bằng không. Phản lực sẽ có hướng ngược lại với hướng của lực tác động ban đầu.
Ngoài ra, điều kiện cân bằng của chất điểm còn phụ thuộc vào môi trường mà nó đang tồn tại. Ví dụ, khi chất điểm đang đứng yên trên mặt đất, nó sẽ phải chịu lực hấp dẫn của Trái Đất. Tuy nhiên, nếu chúng ta đặt chất điểm đó lên một bề mặt nghiêng, thì lực phản lực của bề mặt sẽ được tính đến để duy trì
Cuối cùng, thông qua điều kiện cân bằng, chúng ta có thể tính toán các giá trị vật lý khác nhau, ví dụ như tốc độ, gia tốc, vận tốc, lực tác động và nhiều giá trị khác. Việc áp dụng điều kiện cân bằng vào các bài toán vật lý sẽ giúp chúng ta giải quyết các vấn đề phức tạp và áp dụng kiến thức vật lý vào thực tế.
3. Bài tập vận dụng:
Câu 1: Cho ba lực đồng phẳng, đồng quy F1→, F2→, F3→ có độ lớn lần lượt là 16 N, 12 N và 12 N. Biết góc tạo bởi các lực (F1→ , F2→) = 30° và (F2→ , F3→) = 120°. Độ lớn hợp lực của ba lực này là
A. 27,62 N.
B. 10 N.
C. 16 N.
D. 20 N.
Câu 2: Cho ba lực đồng quy, cùng độ lớn F và cùng nằm trong một mặt phẳng. Biết góc tạo bởi các lưc (F1→, F2→) = (F2→, F3→) = 120°. Hợp lực của chúng bằng
A. 0.
B. F.
C. 2F.
D. 3F.
Câu 3: Một vật chịu tác dụng của bốn lực đồng phẳng, đồng quy nằm ngang gồm lực F1 = 10 N hướng về phía Tây, lực F2 = 36 N hướng về phía Bắc, lực F3 = 22 N hướng về phía Đông, lực F4 = 20 N hướng về phía Nam. Độ lớn của hợp lực do các lực này tác dụng lên vật là
A. 28 N.
B. 20 N.
C. 4 N.
D. 26,4 N.
Câu 4: Một lực có độ lớn 12 N được phân tích thành hai lực F1→ và F2→. Biết các lực tạo với nhau một góc là: (F1→, F2→) = 150° và F2 có giá trị lớn nhất. Độ lớn của các lực F1→ và F2→ lần lượt là
Câu 5: Hai lực F1→ và F2→ vuông góc với nhau. Các độ lớn là 3N và 4N. Hợp lực của chúng tạo với hai lực này các góc bao nhiêu? (lấy tròn tới độ)
A. 30° và 60°
B. 42° và 48°
C. 37° và 53°
D. Khác A, B, C
Câu 6: Hợp lực của hai lực có độ lớn F và 2F có thể
A. nhỏ hơn F
C. vuông góc với lực F→
B. lớn hơn 3F
D. vuông góc với lực 2F→
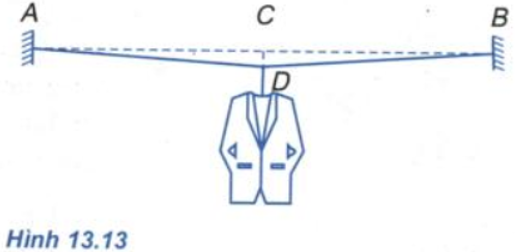
Câu 7: Một chiếc mắc áo treo vào điểm chính giữa của dây thép AB. Khối lượng tổng cộng của mắc và áo là 3kg (Hình 13.13). Biết AB = 4m, CD = 10cm. Tính lực kéo mỗi nửa sợi dây.
A. F1 = F2 = 300,37N.
B. F1 = F2 = 300,00N.
C. F1 = F2 = 150,37N.
D. F1 = F2 = 400,37N.
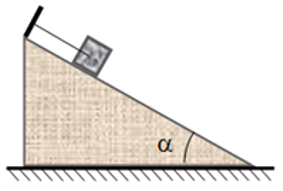
Câu 8: Một vật được giữ như trên hình. Vật nặng 5 kg và lực do thanh tác dụng lên vật là 25 N. Xác định góc α, biết g = 10 m/s2.
A. 60°
B. 30°
C. 45°
D. 15°
Câu 9: Cho vật được đỡ bởi hai thanh như hình vẽ. Biết gia tốc trọng trường g = 10 m/s2. Lực do thanh (1) tác dụng lên vật là 50 N. Khối lượng vật là
A. 2,5 kg.
B. 5 kg.
C. 7,5 kg.
D. 10 kg.
Câu 10: Một vật có khối lượng 1 kg được giữ yên trên mặt phẳng nghiêng bởi một sợi dây song song với đường dốc chính. Biết α = 60°. Cho g = 9,8 m/s2. Lực ép của vật lên mặt phẳng nghiêng là
A. 9,8 N.
B. 4,9 N.
C. 19,6 N.
D. 8,5 N.
Câu 11: Khi nói về phép phân tích lực, phát biểu nào sau đây sai?
A. Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
B. Khi phân tích một lực thành hai lực thành phần thì phải tuân theo quy tắc hình bình hành.
C. Khi phân tích một lực thành hai lực thành phần thì hai lực thành phần làm thành hai cạnh của hình bình hành.
D. Phân tích lực là phép thay thế các lực tác dụng đồng thời vào vật bằng một lực như các lực đó.
Chọn D.
Câu 12: Một chất điểm chịu tác dụng đồng thời của hai lực thành phần có độ lớn F1 và F2 thì hợp lực F→ của chúng luôn có độ lớn thỏa mãn hệ thức:
Chọn B.
Câu 13: Hai lực đồng quy F1→ và F2→ hợp với nhau một góc α, hợp lực của hai lực này có độ lớn là
Chọn D.
Câu 14:Một chất điểm chuyển động dưới tác dụng của hai lực có giá đồng quy F1→ và F2→ thì vectơ gia tốc của chất điểm
A. cùng phương, cùng chiều vs lực F2→.
B. cùng phương, cùng chiều với lực F1→.
C. cùng phương, cùng chiều với phương và chiều của hợp lực giữa F1→ và F2→.
D. cùng phương, ngược chiều với phương và chiều của hợp lực giữa F1→ và F2→.
Chọn C.
Câu 15: Một chất điểm chịu tác dụng đồng thời của hai lực thành phần vuông góc với nhau có độ lớn lần lượt là F1 = 15 N và F2. Biết hợp lực trên có độ lớn là 25 N. Giá trị của F2 là
A. 10 N.
B. 20 N.
C. 30 N.
D. 40 N.
Chọn B.
Câu 16: Hai lực có giá đồng quy có độ lớn là 3 N là 4 N và có phương vuông góc với nhau. Hợp lực của hai lực này có độ lớn là
A. 7 N.
B. 5 N.
C. 1 N.
D. 12 N.
Chọn B.
Câu 17:Hai lực có giá đồng quy có độ lớn F1 = F2 = 10 N, có (F1→, F2→) = 60°. Hợp lực của hai lực này có độ lớn là
A. 17,3 N.
B. 20 N.
C. 14,1 N.
D. 10 N.
Chọn A.
Câu 18: Hai lực có giá đồng quy có độ lớn 7 N và 13 N. Độ lớn hợp lực của hai lực này không thể có giá trị nào sau đây?
A. 7 N.
B. 13 N.
C. 20 N.
D. 22 N.
Chọn D.
Câu 19: Một chất điểm chịu tác dụng của hai lực thành phần có độ lớn 6 N là 8 N. Biết hợp lực của hai lực này có giá trị 10 N, góc tạo bởi hai lực này là
A. 90o.
B. 30o.
C. 45o.
D. 60o.
Chọn A.
Câu 20: Một chất điểm chịu tác dụng của ba lực đồng phẳng, đồng quy có cùng độ lớn 15 N. Biết góc tạo bởi các lực (F1→, F2→) = (F2→, F3→) = 60°. Hợp lực của ba lực này có độ lớn là
A. 30 N.
B. 20 N.
C. 15 N.
D. 45 N.
Chọn A.