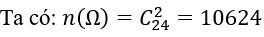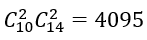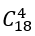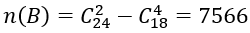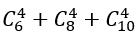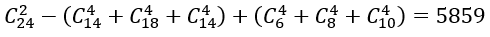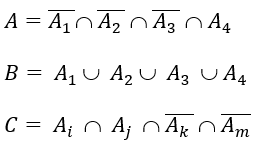Phép thử là gì? Biến cố là gì? Xác suất của biến cố? Toán 11

1. Phép thử là gì? 

Phép thử là một thí nghiệm (hành động, thử nghiệm) mà kết quả xảy ra có tính ngẫu nhiên, không đoán trước được. Mặc dù vậy, ta vẫn có thể xác định được tập hợp tất cả các kết quả của phép thử đó. Phép thử là cách gọi tắt của “phép thử ngẫu nhiên”.Phép thử được kí hiệu bằng chữ “T”.

Không gian mẫu được kí hiệu là Ω, là tập hợp tất cả các kết quả có thể xảy ra của một phép thử nào đó.

Chẳng hạn, tung một con xúc xắc 6 mặt được coi là một phép thử, kết quả thu được là xuất hiện mặt 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm, khi đó ta có: Ω = {1;2;3;4;5;6}

Hay khi ta tung thử đồng xu hai mặt lên cũng được xem là một phép thử, lúc này ta được: Ω = {ngửa; sấp}.

2. Biến cố là gì?

2.1. Định nghĩa: 

Giả sử Ω là không gian mẫu của một phép thử ngẫu nhiên T.

– Nếu A là tập hợp con của Ω thì ta nói A là biến cố

– Trong kết quả của việc thực hiện phép thử T, nếu có một phần tử nào của biến cố xảy ra thì các em có thể nói “biến cố A xảy ra”.

Ví dụ: trong tình huống của ví dụ 1, không gian mẫu của con súc sắc Ω = {1;2;3;4;5;6}

Gọi A là biến cố “Các mặt xuất hiện chấm chẵn”. Khi đó A = {2;4;6}

Hay trong tình huống của ví dụ 3, khi tung đồng xu 2 lần, gọi A là biến cố “cả hai lần xuất hiện mặt khác nhau” thì A = {SN; NS;}

2.2. Phân loại: 

Có rất nhiều loại biến cố, tuy nhiên bài học này, chúng tôi sẽ đi sâu vào phân tích ba loại biến cố thường gặp và phổ biến trong đề thi nhất, đó là: biến cố chắc chắc và biến cố không thể, biến cố ngẫu nhiên

– Biến cố chắc chắn là biến cố chắc chắn xảy ra trong một phép thử.

– Biến cố không thể là biến cố không thể xảy ra trong một phép thử

– Biến cố ngẫu nhiên là biến cố có thể hoặc không thể xảy ra trong một phép thử

Giả sử Ω là không gian mẫu của phép thử ngẫu nhiên T, ta có các định nghĩa như sau:

– Biến cố A được gọi là biến cố ngẫu nhiên, nếu A ≠ Ø (rỗng) và A là tập con của Ω.

– Tập không gian mẫu Ω được gọi là biến cố chắc chắn.

– Tập rỗng Ø được gọi là biến cố không thử (gọi tắt là biến cố không).

Ngoài những biến cố thường gặp trên, còn một số loại biến cố:

– Biến cố sơ cấp: Biến cố A được gọi là biến cố sơ cấp nếu nó không có biến cố cố nào thuận lợi cho nó (trừ chính nó), tức là không thể phân tích được nữa.

Ví dụ: Xét phép thử “tung một đồng xu 2 lần”, biến cố A: “cả 2 lần xuất hiện mặt sấp” và biến cố B: “cả hai lần xuất hiện mặt ngửa” gọi là các biến cố sơ cấp. Còn biến cố C: “tung được hai mặt giống nhau” không là biến cố sơ cấp vì C có thể phân tích thành A⋃B.

– Biến cố hiệu: Là hiệu của hai biến cố A và B, kí hiệu A-B (hay A\B) là một biến cố xảy ra khi và chỉ khi A xảy ra nhưng B không xảy ra.

2.3. Phép toán giữa các biến cố trong cùng 1 phép thử:

Giả sử Ω là không gian mẫu của phép thử T và E, F là các biến cố cùng liên quan đến phép thử T, ta có các định nghĩa và các kết quả sau:

Biến cố đồng nhất:

Định nghĩa: Hai biến cố E và F là đồng nhất hay tương đương với nhau khi và chỉ khi “Tập E bằng tập F”. Kí hiệu: E = F

Hợp và giao giữa các biến cố:

Giả sử E, F là hai biến cố bất kì của cùng một phép thử T. Ta có định nghĩa sau:

– Tập E U F được gọi là hợp của các biến cố E và F. E U F xảy ra khi và chỉ khi E xảy ra hoặc F xảy ra.

– Tập E ⋂ F được gọi là giao của các biến cố E và F. E ⋂ F xảy ra khi và chỉ khi E và F đồng thời xảy ra. Biến cố E F còn được viết là E.F.

Hai biến cố xung khắc:

Hai biến cố E và F là xung khắc với nhau khi và chỉ khi chúng không khi nào cùng xảy ra hay E ⋂ F = Ø.

Biến cố đối

Định nghĩa: Nếu E là biến cố liên quan đến phép thử T thì tập Ω \ E cũng là một biến cố liên quan đến phép thử T và được gọi là biến cố đối của biến cố E, kí hiệu là Ē.

Chú ý: Từ định nghĩa trực tiếp suy ra: Ē = “Không xảy ra biến cố E”.

Từ đó ta có: Ē xảy ra <=> E không xảy ra.

Ē là phần bù của E trong Ω.

F là biến cố đối của biến cố E thì E là biến cố đối của biến cố F (E và F là hai biến cố đối nhau).

Đồng thời ta có:

( E và F là hai biến cố đối nhau) <=> E U F = Ω và E ⋂ F = ∅

Chẳng hạn: Khi gieo đồng xu hai lần

Gọi E là biến cố:”Đồng xu hai lần giống nhau” ⟹ E = {SS; NN}.

Gọi F là biến cố:”Đồng xu hai lần khác nhau” ⟹ F = {SN, NS}.

Ta thấy E U F = Ω và E ⋂ F = ∅ nên E và F là biến cố đối của nhau.

3. Xác xuất của biến cố là gì?

“Xác suất” chỉ xét với các phép thử ngẫu nhiên có hữu hạn kết quả có thể xảy ra.

Giả sử A là biến cố liên quan đến phép thử T và phép thử T có một số hữu hạn kết quả có thể có, đồng khả năng. Khi đó ta gọi tỉ số 

là xác suất của biến cố A. Kí hiệu là  .

Trong đó:

– n(A) là số phần tử của tập hợp A, cũng chính là số các kết quả có thể có của phép thử T thuận lợi cho biến cố A

–  là số phần tử của không gian mẫu Ω, cũng chính là số các kết quả có thể có của phép thử T.

Tính chất:

Quy tắc cộng xác suất:

– A, B xung khắc  hay   ) thì