Thể tích là gì? Đơn vị đo thể tích? Công thức tính thể tích?

Bạn đang xem: Thể tích là gì? Đơn vị đo thể tích? Công thức tính thể tích? tại truongptdtntthptdienbiendong.edu.vn

Thể tích của một hình được áp dụng rất nhiều trong cuộc sống hiện nay. Vậy thể tích là gì? Thể tích được đo bằng đơn vị nào? Những công thức tính thể tích? Bài viết dưới đây sẽ cung cấp cho các bạn những kiến thức cơ bản nhất về thể tích.

1. Thể tích là gì?

Thể tích của một vật đó là lượng không gian mà một vật đó chiếm. Tuy nhiên, bạn cần phải phân biệt được hai khái niệm về thể tích và dung tích. Đây là hai khái niệm hoàn toàn khác nhau và rất dễ bị nhầm lẫn.

Dung tích là khả năng chứa đựng tối đa của một vật nào đó. Ví dụ như dung tích của một chai nước là khả năng chứa nước tối đa của cái chai nước đó.

Thể tích của một vật được ký hiệu là V. Bạn cần lưu ý khi viết ký hiệu là V (in hoa) để phân biệt với v (thường) đây là ký hiệu của vận tốc.

2. Đơn vị đo thể tích:

Đơn vị của thể tích được đo chủ yếu là mét khối, ký hiệu là m³ và lít có ký hiệu là l.

Ngoài đơn vị là mét khối ( m³), thì người ta có thể dùng các đơn vị đo khác nhỏ hơn như là cm³ hay dm³.

Tương tự như mét khối, bên cạnh lít, người ta có thể dùng đơn vị đo khác nhỏ hơn là mililít, ký hiệu là ml hoặc sử dụng đơn vị lớn hơn là megalít, ký hiệu là ML. Các bạn cần để ý kỹ để phân biệt sự khác nhau về ký hiệu giữa hai đại lượng này nhằm tránh nhầm lẫn.

Mối liên hệ giữa các đơn vị đo của thể tích:

1 lít = 1 dm³

1 cm³ = 1 ml

1 lít = 1 dm³ = 1000 cm³ = 1000 ml

1 m³ = 1000 lít = 1000 dm³ = 1000000 cm³ = 1000000 ml

Các đơn vị đo thể tích thường được dùng với các chất lỏng như: nước, xăng, dầu…:

1 m³ = 1000 dm³, 1 dm³ = 1/1000 m³

1 dm³ = 1000 cm³, 1 cm³ = 1/1000 dm³

1 cm³ = 1000 mm³, 1 mm³ = 1/1000 cm³

Mỗi đơn vị đo thể tích gấp 1000 lần đơn vị bé liền sau.

Mỗi đơn vị đo thể tích bằng 1/1000 đơn vị lớn liền trước.

3. Công thức tính thể tích:

3.1. Công thức tính thể tích vật lý:

Trong vật lý, công thức tính thể tích được xác định như sau:

V = m/ D

Trong đó:

V là thể tích

m là khối lượng của vật

D là khối lượng riêng của chất tạo thành vật đó.

Do đó, ta có thể xác định được mối quan hệ giữa thể tích và khối lượng của vật đó là mối quan hệ tỉ lệ thuận.

3.2. Cách tính thể tích chất lỏng:

Cách tính thể tích của chất lỏng hay cách tính thể tích của nước sẽ phải phụ thuộc vào vật chứa số chất lỏng đó để có thể tính một cách chính xác nhất. Nếu vật chứa chất lỏng là hình hộp chữ nhật thì ta cần áp dụng công thức tính thể tích hình hộp chữ nhật để tính toán thể tích. Tương tự như vậy, nếu đó là hình lập phương hay hình trụ thì ta áp dụng công thức tính thể tích của hình lập phương và hình trụ để tính toán thể tích.

Như vậy, sẽ không có một công thức cụ thể nào để tính thể tích của chất lỏng hay nước mà cách tính thể tích của chất lỏng nói chung và của nước nói riêng sẽ phụ thuộc vào vật chứa loại chất lỏng đó.

3.3. Một số công thức tính thể tích của các hình phổ biến:

Thể tích hình hộp chữ nhật: được tính bằng tích của diện tích đáy và chiều cao.

V = a.b.h

Trong đó:

V là thể tích của hình hộp chữ nhật.

a là chiều dài của hình hộp chữ nhật.

b là chiều rộng của hình hộp chữ nhật.

h là chiều cao của hình hộp chữ nhật.

Thể tích hình lập phương: bằng cạnh a mũ 3 lần.

V = a.a.a hay V = a^³

Trong đó:

V là thể tích của hình lập phương.

a là độ dài cạnh của hình lập phương.

Thể tích hình lăng trụ đứng: bằng tích diện tích đáy nhân với chiều cao.

V = S.h

Trong đó:

V là thể tích hình lăng trụ đứng.

S là diện tích đáy hình lăng trụ đứng.

h là chiều cao hình lăng trụ đứng.

Thể tích hình cầu: dựa theo kích thước bán kính của khối cầu.

V = 4/3.π.r^³

Trong đó:

V là thể tích khối cầu.

π là số pi, có giá trị bằng 3,14.

r là bán kính khối cầu

Thể tích khối chóp: tính diện tích đáy và tính chiều cao

V = 1/3.S.h

Trong đó:

V là thể tích khối chóp

S là diện tích đáy khối chóp

h là chiều cao khối chóp.

4. Một số câu hỏi trắc nghiệm:

Câu 1: Thể tích của khối chóp có chiều cao bằng h và diện tích đáy bằng B là:

A. V= (1/2).B.h

B. V= (1/3).B.h

C. V= (2/3).B.h

D. V= (1/6).B.h

Hướng dẫn giải: Đáp án B. Áp dụng công thức.

Câu 2: Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối chóp đã cho bằng bao nhiêu?

A. V= 4a³

B. V= (2/3).a³

C. V= a³

D. V= (4/3).a³

Hướng dẫn giải: Đáp án B.

Diện tích hình vuông là: S = a²=> Thể tích khối chóp đó là: S = (1/3).B.h= (1/3).2a.a² = (2/3).a³

Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, có SA là chiều cao. Biết SA= 5, AB= 4, BC= 3. Tính thể tích khối chóp đó.

A. V= 10

B. V= 15

C. V= 5

D. V=12

Hướng dẫn giải: Đáp án A.

Xét tam giác ABC vuông tại B nên diện tích đáy bằng:

S = ½. AB.BC = ½.4.3 = 6

Thể tích hình chóp S.ABC đó là: V = 1/3.B.h = 1/3.6.5 = 10

Câu 4: Cho hình lập phương có cạnh bằng 3. Tính thể tích hình lập phương đó.

A. V= 9

B. V=10

C. V=27

D. V=15

Hướng dẫn giải: Đáp án C.

Thể tích hình lập phương đó là: V = a.a.a = a³ = 3.3.3 = 27

Câu 5: Cho hình hộp chữ nhật ABCD có chiều dài 8 cm, chiều rộng 5 cm và chiều cao bằng ½ chiều dài. Thể tích của hình hộp chữ nhật ABCD bằng bao nhiêu?

A. V= 40 cm³

B. V= 50 cm³

C. V= 80cm³

D. V= 160 cm³

Hướng dẫn giải: Đáp án D.

Chiều cao của hình hộp chữ nhật ABCD là: h = ½.8 = 4 cm.

Thể tích hình hộp chữ nhật ABCD là: V = 8.5.4 = 160 cm³.

Câu 6: Cho hình lăng trụ đứng có đáy là tam giác vuông có 2 cạnh góc vuông lần lượt là 5 và 6. Biết chiều cao hình lăng trụ là 4. Tính thể tích hình lăng trụ đó.

A. V = 60

B. V = 120

C. V = 100

D. V = 90

Hướng dẫn giải: Đáp án A

Diện tích hình lăng trụ đó là: S = ½.5.6 = 15

Thể tích hình lăng trụ đó là: V = S.h = 15.4 = 60

Bài tập 7: Cho hình cầu có đường kính bằng 6. Tính thể tích hình cầu đó?

A. V = 36π

B. V = 42π

C. V = 12π

D. V= 27,5π

Hướng dẫn giải: Đáp án A.

Bán kính hình cầu đó là: r = d/2 = 3

Thể tích hình cầu đó là: V = 4/3.π.r³ = 36π

5. Bài tập tự luận:

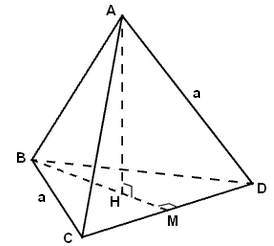
Bài tập 1: Cho một khối tứ diện đều có cạnh bằng a. Tính thể tích khối tứ diện đó?

Hướng dẫn giải:

bài 1 trang 25 sgk hình học 12

Giả sử ABCD là tứ diện đều có cạnh bằng a.

Gọi điểm H là tâm đường tròn ngoại tiếp tam giác BCD.

Ta có: HB = HC =HD => Điểm H nằm trên trục đường tròn ngoại tiếp tam giác BCD.

Xét tứ diện đều ABCD, ta có: AB = AC = AD.

=> AH là trục đường tròn ngoại tiếp tam giác BCD => AH vuông góc với (BCD)

Vì tam giác BCD là tam giác đều nên ta có H là trọng tâm tam giác BCD.

Gọi điểm M là trung điểm của cạnh CD, ta xét tam giác BCD có:

Ta lại có:

Áp dụng định lý Pytago vào tam giác vuông AHB, ta có:

Diện tích tam giác đều BCD có cạnh bằng a là:

Thể tích khối tứ diện đều ABCD là:

Bài tập 2: Tính tỉ số thể tích khối lăng trụ và thể tích khối chóp khi có diện tích đáy bằng với chiều cao?

Hướng dẫn giải:

bài 4 trang 26 sgk hình học 12

Giả sử hình lăng trụ và hình chóp trên có diện tích đáy bằng S và chiều cao bằng h.

Thể tích của khối lăng trụ là: V1 = S.h

Thể tích của khối chóp là: V2 = 1/3.S.h

Tỉ số thể tích khối lăng trụ và thể tích khối chóp là:

Bài tập 3: Cho khối lăng trụ tam giác đều ABC. A1B1C1 có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh AA1. Tính thể tích khối chóp M.BCA1 ?

Hướng dẫn giải:

Vì tam giác ABC là tam giác đều có cạnh bằng a nên diện tích tam giác ABC là: S = (a²√3)/ 4

Ta có: AM = AA1/2 = a/2

Vì hai tứ diện MABC và tứ diện MBCA1 có chung đỉnh C, có diện tích hai đáy MAB và MA1B bằng nhau nên thể tích MABC và thể tích MBCA1 cũng bằng nhau, suy ra:

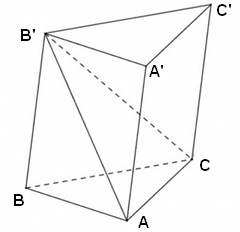
Bài tập 4: Cho hình lăng trụ ABC.A’B’C’ có A’ABC là hình chóp tam giác đều có cạnh đáy AB bằng a. Biết độ dài đoạn vuông góc chung của AA’ và BC là (a√3)/4. Thể tích khối chóp A’BB’C’C bằng bao nhiêu?

Hướng dẫn giải: