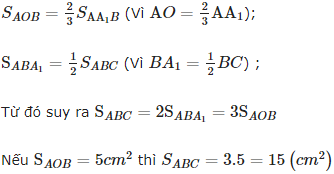Trọng tâm là gì? Tính chất và cách tính trọng tâm tam giác?

1. Trọng tâm là gì?

1.1. Trọng tâm là gì?

Trọng tâm là tâm điểm của một hình, hay nói cách khác trọng tâm của một vật thể là điểm mà nếu bạn đặt một trụ thẳng vào điểm đó thì vật thể đó sẽ có thể đứng một cách cân bằng.

Trọng tâm là một ứng dụng được sử dụng phổ biến trong thực tế đời sống. Với toán học, trọng tâm là một trong các tính chất rất quan trọng, đặc biệt là với hình tam giác.

1.2. Trọng tâm trong tam giác là gì?

Trọng tâm của tam giác là tâm điểm của hình tam giác, là giao điểm của ba đường trung tuyến của hình tam giác đó. Trong đó đường trung tuyến là đường nối từ một đỉnh đến trung điểm của cạnh đối diện. 

Theo sách giáo khoa lớp 7, thì trọng tâm tam giác được định nghĩa rằng: “Trong 1 tam giác có 3 đường trung tuyến. 3 đường trung tuyến này cùng đi qua một điểm, điểm này được gọi là trọng tâm của tam giác”.

2. Tính chất của trọng tâm:

Tinh chất quan trọng nhất của trọng tâm chính là: “Khoảng cách từ trọng tâm đến ba đỉnh của tam giác bằng ⅔ độ dài đường trung tuyến ứng với đỉnh đó”.

Như hình vẽ, ta có tam giác ABC, trọng tâm G, P,M,N lần lượt là trung điểm của các cạnh AB,BC,AC, nên các đường trung tuyến sẽ là CP, AM, BN. 

Như tính chất trên thì ta có:

GA = 2/3 AM

GB = 2/3 AN

GC = 2/3 CP

– Quy tắc trọng tâm tam giác theo vecto:

Trọng tâm tam giác được xác định là giao điểm của ba đường trung tuyến trong tam giác. Vì thế áp dụng quy tắc vecto ta sẽ có:

Sử dụng hình vẽ trên với điểm G là trọng tâm tam giác ABC thì ta có: 

với mọi điểm M bất kỳ.

3. Cách xác định trọng tâm:

Dựa theo định nghĩa và tính chất của trọng tâm, ta có hai cách vẽ trọng tâm tam giác như sau: 

Cách 1: xác định trọng tâm tam giác dựa theo tính chất (trọng tâm tam giác là giao điểm của ba đường trung tuyến)

Bước 1: vẽ tam giác ABC

Bước 2: xác định trung điểm P,M,N lần lượt của các cạnh AB,BC,AC

Bước 3: Nối A với trung điểm M của cạnh BC, làm tương tự nối B với trung điểm N của cạnh AC, và nối C với trung điểm P của cạnh AB.

Bước 4: sau khi thực hiện bước 3 như trên, ta sẽ được ba đường trung tuyến AM, BN, CP của tam giác ABC, giao điểm của ba đường trung tuyến này đặt tên là G và đây chính là trọng tâm của tam giác ABC.

Lưu ý: ba đường trung tuyến này chắc chắn sẽ đồng quy tại một điểm, nếu bạn không vẽ được chúng đồng quy thì có thể bạn đã xác định sai trung điểm ở bước 2.

Cách 2: dựa trên tính chất của trọng tâm tam giác: “Khoảng cách từ trọng tâm đến ba đỉnh của tam giác bằng ⅔ độ dài đường trung tuyến ứng với đỉnh đó”.

Bước 1: vẽ tam giác ABC

Bước 2: xác định trung điểm M của cạnh BC

Bước 3: nối A với M để tạo thành trung tuyến AM của tam giác ABC

 Bước 4: xác định điểm G thuộc cạnh AM sao cho AG = ⅔ AM.

Và G chính là trọng tâm của tam giác ABC.

4. Trọng tâm của một số hình đặc biệt:

4.1. Trọng tâm của tam giác cân:

Xét tam giác ABC cân tại AM với M là trung điểm của BC và G là trọng tâm của tam giác ABC. Ta có: AG vừa là đường trung tuyến vừa là đường phân giác của góc BAC và là đường cao của tam giác ABC => AG vuông góc với BC.

4.2. Trọng tâm của tam giác vuông:

Xét tam giác ABC vuông tại A, I là trung điểm của BC và G là trọng tâm tam giác ABC như hình vẽ dưới đây:

Ta sẽ được AI = ½ BC = BI = CI

Chứng minh điều này rất đơn giản: ta vẽ đường tròn tâm I và đường kính BC, A,B,C là các điểm thuộc đường tròn mà BC là đường kính nên tam giác ABC vuông tại A, từ đây ta có AI,BI,CI là các đường bán kính của đường tròn nên AI = BI = CI.

Từ tính chất trên ta cũng được tam giác ABI và tam giác ACI đều cân tại I và AMIN sẽ tạo thành một hình chữ nhật.

4.3. Trọng tâm của tam giác đều:

Tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác.

Vì vậy theo tính chất của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

5. Một số bài toán áp dụng trọng tâm tam giác:

Bài 1: Cho tam giác MNP cân tại M, có MH vuông góc với NP. Chứng minh MH là đường trung tuyến của tam giác MNP.

Đáp án:

Xét tam giác MNH vuông tại H và tam giác MPH vuông tại H có:

MN = MP ( Vì tam giác MNP cân tại M)

AH là cạnh chung

Do đó, tam giác MNH = tam giác MPH ( cạnh huyền- cạnh góc vuông)

Suy ra NH = PH (hai cạnh tương ứng)

Suy ra H là trung điểm của NP

Vậy MH là đường trung tuyến của tam giác MNP.

Bài 2: Cho tam giác DEF có M, N lần lượt là trung điểm của DE và DF. Biết FM và EN cắt nhau tại H. Chứng minh DH là đường trung tuyến của tam giác DEF.

Đáp án:

Vì M, N lần lượt là trung điểm của DE và EF nên FM và EN là hai đường trung tuyến của tam giác DMN.

Mà FM và EN cắt nhau tại H nên DH là đường trung tuyến thứ ba của tam giác DEF.

Bài 3: Cho tam giác ABC vuông tại A với G là trọng tâm. Chứng minh rằng hai tam giác AIB và tam giác AIC là tam giác cân.

Đáp án:

Xét tam giác ABC vuông tại A với G là trọng tâm. Vì AI là đường trung tuyến của một góc vuông nên ta có: AI = 1/2 BC = BI = CI.

Suy ra, tam giác AIB và tam giác AIC lần lượt cân tại I.

Bài 4: Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính cách từ đỉnh A tới trọng tâm G của tam giác ABC.

Đáp án:

Gọi M là trung điểm của BC

Suy ra: AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên A M = 1/2BC

BC = √ (AB^2 + AC^2) = √ ( 3^2 + 4^2 ) = 5 cm

⇒ A M = 1 / 2 x 5 = 2,5 cm

Vì G là trọng tâm của tam giác ABC nên AG = 2/3 AM = 2/3 .2,5 = 1,7 cm.

Vậy AG = 1,7 cm.

Bài 5: Cho tam giác ADP có hai đường trung tuyến DE và PF cắt nhau ở G. AG kéo dài cắt PD ở M. Chứng minh MP = MD.

Đáp án:

Vì tam giác ADP có hai đường trung tuyến cắt nhau tại G, suy ra G là trọng tâm tam giác ADP.

Mà AM đi qua G nên AM là đường trung tuyến thứ ba.

Suy ra M là trung điểm của DP

Vậy MD = MP.

Bài 6: Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.

Đáp án: 

Gọi trung điểm MN, MP, PN lần lượt là R, O, S.

Khi đó MS, PR, NO đồng quy tại trọng tâm I.

Ta có ∆MNP đều, suy ra:

MS = PR = NO (1).

Vì I là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:

MI = 2/3 MS, PI = 2/3 PR, NI = 2/3 NO (2).

Từ (1) , (2) ⇒ GA = GB = GC.

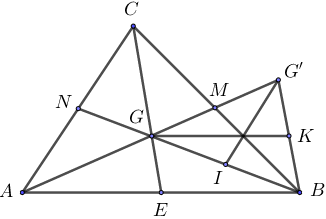
Bài 7: Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.

a) So sánh các cạnh của  tam giác BGG’ với các đường trung tuyến của tam giác ABC

b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Đáp án:

a) So sánh các cạnh của  ∆BGG’ với các đường trung tuyến của  ∆ABC BG cắt AC tại N

CG cắt AB tại E

G là trọng tâm của  ∆ABC

$\Rightarrow GA=\frac{2}{3}AM$

Mà GA = GG’ (G là trung điểm của AG’)

.$\Rightarrow G{G}^{\prime }=\frac{2}{3}AM$.

Vì G là trọng tâm của  ∆ABC $\Rightarrow GB=\frac{2}{3}BN$

Mặt khác: $GM=\frac{1}{2}AG$ (G là trọng tâm)

$AG=G{G}^{\prime }\Rightarrow GM=\frac{1}{2}G{G}^{\prime }$

M là trung điểm của GG’

Do đó $\Delta GMC=\Delta G^{\prime }MB$ vì:

$\begin{array}{c}GM=M{G}^{\prime }\\ MB=MC\\ \angle GMC=\angle G^{\prime }MB\\ \Rightarrow B{G}^{\prime }=CG\end{array}$

Mà $CG=\frac{2}{3}CE$ (G là trọng tâm tam giác ABC)

$\Rightarrow B{G}^{\prime }=\frac{2}{3}CE$

Vậy mỗi cạnh của ∆BGG’ bằng $\frac{2}{3}$

b)  So sánh các đường trung tuyến của ∆BGG’ với cạnh ∆ABC

Ta có: BM là đường trung tuyến ∆BGG’

Mà M là trung điểm của BC nên $BM=\frac{1}{2}BC$

Vì $IG=\frac{1}{2}BG$ (I là trung điểm BG)

$GN=\frac{1}{2}BG$ (G là trọng tâm)

$\Rightarrow IG=GN$

Do đó $\Delta IG{G}^{\prime }=\Delta NGA\left(c.g.c\right)$

$\Rightarrow I{G}^{\prime }=AN\Rightarrow I{G}^{\prime }=\frac{1}{2}AC$

Gọi K là trung điểm BG $\Rightarrow$ GK là trung tuyến ∆BGG’

Vì $GE=\frac{1}{2}GC$ (G là trọng tâm ∆ABC)

$\Rightarrow GE=\frac{1}{2}BG$

Mà K là trung điểm BG’ $\Rightarrow$ KG’ = EG

Vì ∆GMC = ∆G’BM (chứng minh trên)

$\Rightarrow \angle GCM=\angle G^{\prime }BM$ (lại góc sole trong)

$\Rightarrow CE//B{G}^{\prime }\Rightarrow \angle AGE=\angle A{G}^{\prime }B$ (đồng vị)

Do đó $\Delta AGE=\Delta G{G}^{\prime }K\left(c.g.c\right)\Rightarrow AE=GK$

Mà $AE=\frac{1}{2}AB$ nên $GK=\frac{1}{2}AB$

Vậy mỗi đường trung tuyến ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó.

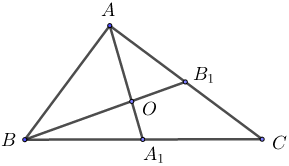
Bài 8: Trong tam giác ABC, hai đường trung tuyến $A{A}_1$ và $B{B}_1$ cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO  bằng $5c{m}^2.$

Đáp án:

Ta có: