Trực tâm là một trong những kiến thức toán học quan trọng đối với học sinh lớp 7, lớp 8, lớp 9, đặc biệt là lớp 10. Vậy trực tâm là gì và thế nào là trực tâm?
Tại đây, đội ĐẢO NGƯỢC Chúng tôi sẽ hướng dẫn các bạn nhận biết thế nào là trực giao và cách chứng minh trực giao rất đơn giản, chi tiết và dễ hiểu qua bài viết dưới đây.
Mục lục bài viết [Ẩn]
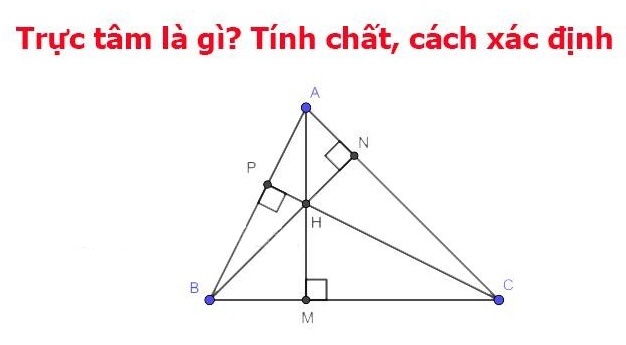
Trung tâm trực tiếp là gì? Công thức trực tâm?
Định nghĩa: Trực tâm là giao điểm của 3 đường cao ứng với 3 đỉnh trong 1 tam giác. Mỗi tam giác chỉ có một trực tâm. Trực tâm có thể nằm trong hoặc ngoài tam giác.
Thiên nhiên: “Khoảng cách từ một đỉnh đến trực tâm của một tam giác gấp hai lần khoảng cách từ tâm đường tròn ngoại tiếp tam giác đó đến trung điểm của cạnh nối hai đỉnh còn lại”. Các dấu hiệu nhận biết như sau:
- Đối với tam giác nhọn: Trực tâm nằm trong miền trong tam giác
- Cho tam giác vuông: Trực tâm là đỉnh của góc vuông
- Đối với tam giác tù: Trực tâm nằm ngoài tam giác
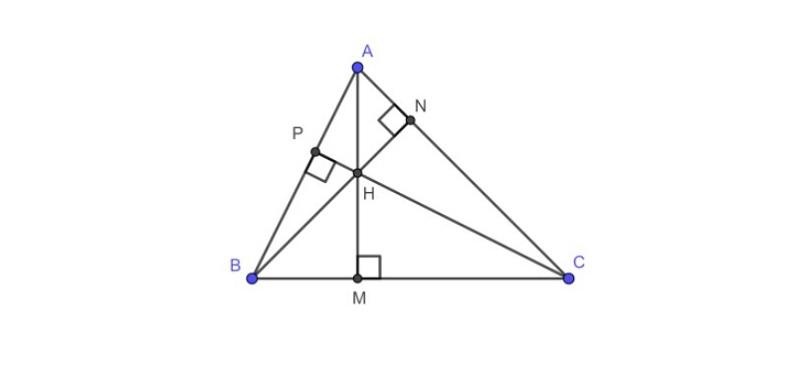
* Công thức tính trực tâm: Sau khi biết trực tâm là gì, chắc hẳn các bạn sẽ có xu hướng tìm kiếm các công thức trực tâm để có thể giải các bài toán một cách dễ dàng. Nhưng trong một số trường hợp đặc biệt, bạn cũng có thể áp dụng công thức tính độ cao trong tam giác cân, tam giác đều, tam giác vuông để suy ra kết quả trực tâm tương ứng. Hãy cùng INVERT tìm hiểu đường cao dưới đây là gì nhé.
Khái niệm đường cao của tam giác
Định nghĩa: Đường cao của tam giác là đoạn vuông góc kẻ từ 1 đỉnh đến đường thẳng chứa cạnh đối diện, độ dài đường cao chính là khoảng cách giữa đỉnh và đáy, theo đó mỗi tam giác sẽ có 3 đường cao.
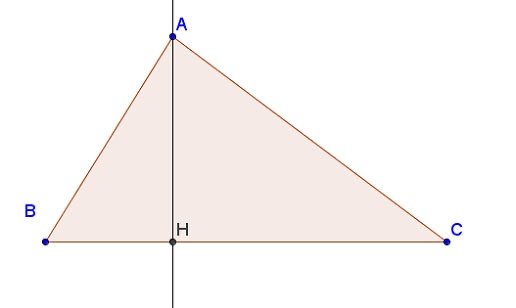
Tính chất của trực tâm của tam giác
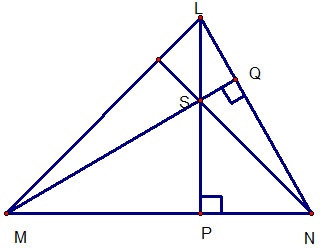
Cho hình vẽ, ba đường cao của tam giác cùng đi qua một điểm S là trực tâm của tam giác LMN. Cụ thể 3 đường cao của tam giác bao gồm các tính chất cơ bản sau:
- Tính năng 1: Trong 1 Tam giác cânđường trung tuyến ứng với cạnh đáy đồng thời là tia phân giác, trung tuyến và đường cao của tam giác đó.
- Tính năng 2: Trong một tam giác nếu có một đường trung tuyến đồng thời là một đường phân giác thì tam giác đó là tam giác cân.
- 3 . tài sản: Trong một tam giác nếu có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác cân.
- Tính năng 4: Trực tâm của tam giác nhọn ABC sẽ trùng với tâm đường tròn nội tiếp tam giác tạo bởi 3 đỉnh lần lượt là chân của 3 đường cao kẻ từ các đỉnh A, B, C đến các cạnh BC, AC, AB.
- Tính năng 5: Đường cao của tam giác ứng với 1 đỉnh cắt đường tròn ngoại tiếp tại điểm thứ 2 sẽ là phép đối xứng của trực tâm qua cạnh tương ứng.
Định lý Carnot: Đường cao của tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ hai là điểm đối xứng của TT qua cạnh tương ứng.
*Kết quả: Trong tam giác đều, trọng tâm, trực tâm, các điểm cách đều ba đỉnh, các điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm bằng nhau.
Ví dụ: Cho tam giác ABC cân tại A, trung tuyến AM và đường cao BK. Gọi H là giao điểm của AM và BK. Chứng minh CH vuông góc với AB.
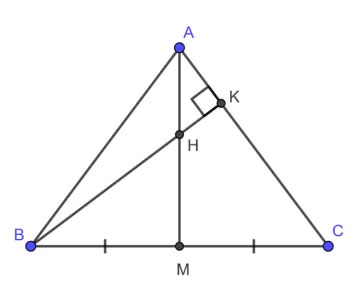
Phần thưởng: Vì tam giác ABC cân tại A nên trung tuyến AM cũng là đường cao của tam giác ABC.
Ta có H là giao điểm của hai đường cao AM và BK nên H là trực tâm của tam giác ABC
=> CH là đường cao của tam giác ABC
Vậy CH vuông góc với AB.
Cách xác định trực tâm trong tam giác
Trong một tam giác, bạn chỉ có thể xác định trực tâm bằng hai đường cao. Theo đó, đối với tam giác tù, tam giác nhọn hay tam giác cân, tam giác đều thì cách xác định trực tâm là như nhau.
Cách xác định: Từ 2 đỉnh của tam giác, bạn vẽ đường cao tương ứng với 2 cạnh đối diện. Khi đó trực tâm của tam giác là giao điểm của hai đường cao đó và chắc chắn đường cao kia cũng đi qua giao điểm này dù không cần vẽ hình.
Cách chứng minh trực tâm của tam giác
1. Trực tâm của tam giác vuông
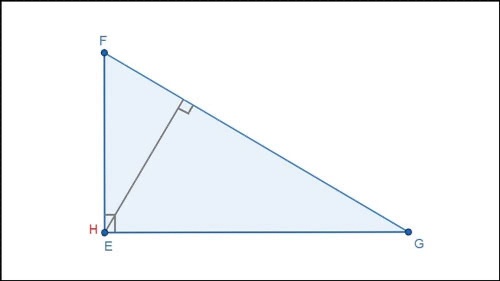
Trực tâm của tam giác vuông là đỉnh của góc vuông.
Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.
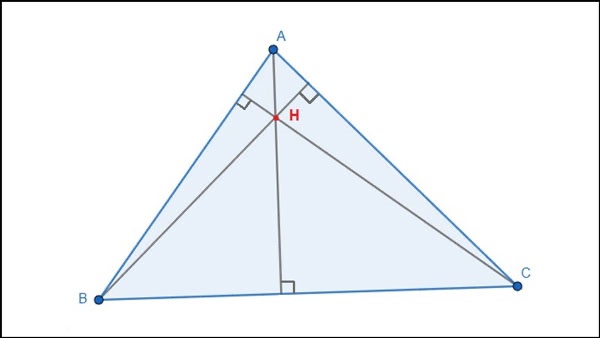
2. Trực tâm của tam giác nhọn
Cho tam giác nhọn ABC có trực tâm H nằm trong tam giác.
3. Trực tâm của tam giác tù
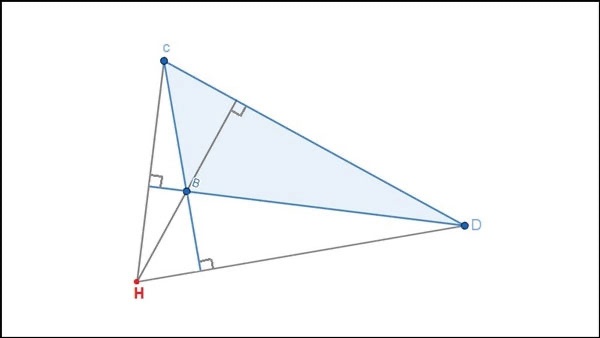
Trực tâm của tam giác tù nằm ngoài tam giác.
Ví dụ: Tam giác tù BCD có trực tâm H nằm ngoài tam giác
V. Một số bài tập về trực tâm
1. Bài tập phương trình có lời giải
Bài tập 1: Cho ΔABC cân tại A, các đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔMED là hình gì?
A. Tam giác cân
B. Tam giác vuông cân
C. Tam giác vuông
D. Tam giác đều.
Trả lời: A
Bài 2: Cho AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C, D sao cho MA = MC, MD = MB. Tia AC cắt BD tại E. Tính số đo góc AEB
A. 300
B. 450
C.600
D.900
Trả lời: DỄ DÀNG
Bài 3: Cho ΔABC vuông tại A, trên cạnh AC lấy các điểm D, E sao cho góc ABD = góc DBE = góc EBC. Trên tia đối của tia DB lấy điểm F sao cho DF = BC. Tam giác CDF là gì?
A. Tam giác cân tại F
B. Tam giác vuông tại D
C. Tam giác cân tại D
D. Tam giác cân tại C
Trả lời: A
Bài 4: Đối với bản vẽ
a) Chứng minh NS LM
b) Khi góc LNP = 50otính góc MSP và góc PSQ.
Phần thưởng:

b)
+ Ta có: trong một tam giác vuông hai góc nhọn phụ nhau nên:
ΔNMQ vuông tại Q có:

Bài 5: Trên đường thẳng d lấy ba điểm phân biệt I, J, K (J nằm giữa I và K).
Vẽ đường thẳng l vuông góc với d tại J. Trên l lấy một điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Chứng minh KN ⊥ IM.
Phần thưởng:
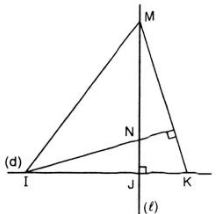
Trong một tam giác, ba đường cao đồng quy tại một điểm là trực tâm của tam giác.

Bài 6: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Chỉ ra các đường cao của tam giác HBC. Từ đó, chỉ ra trực tâm của tam giác đó.
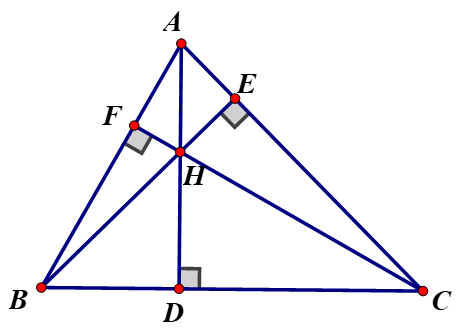
Phần thưởng: Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ A, B, C của ∆ABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
ΔHBC có:
AD ⊥ BC nên AD là đường cao kẻ từ H đến BC.
BA HC tại F nên BA là đường cao kẻ từ B đến HC
CA ⊥ BH tại E nên CA là đường cao kẻ từ C đến HB.
AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.
Bài 7: Cho △ABC có các đường cao AD; BE; CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.
a) Chứng minh: JT⊥EFJT⊥EF
b) Chứng minh: IE⊥JEIE⊥JE
c) Chứng minh: DA là tia phân giác của góc EDF.
d) Gọi P; Q là hai điểm đối xứng của D qua AB và AC .
Chứng minh: P; F; E; Q thẳng hàng.
Câu trả lời:
a) Sử dụng tính chất đường trung tuyến trong tam giác vuông, ta có:
FI = 12AH = EIFJ = 12BC = EJFI = 12AH = EIFJ = 12BC = EJ
Vậy IJ là tia phân giác của EF
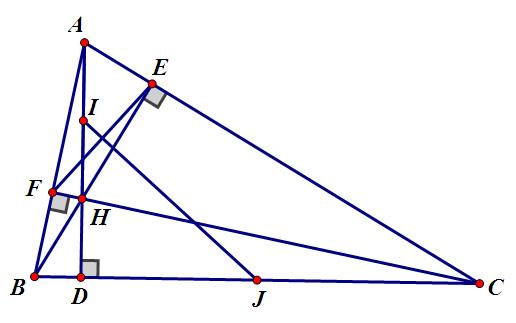
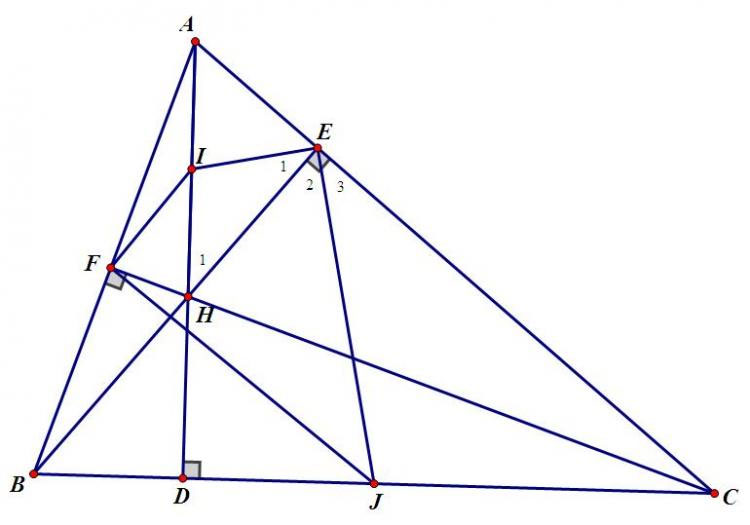
b)
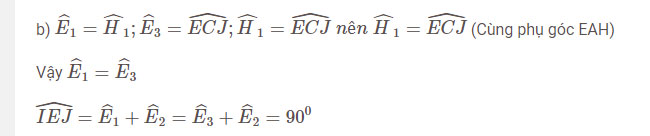
c) Tứ giác BFHD và ABDE nội tiếp (đpcm)
d) H là giao điểm ba đường phân giác của tam giác EFD
Góc PFB = BFD
Góc DFH = EFH
4 góc này cộng lại = 2.90 = 180 => P,E,F thẳng hàng
Tương tự ta có F, E, Q thẳng hàng.
2. Bài tập trực giao không có lời giải

Trên đây là Một số lý thuyết & giải pháp về trực tâm mà nhóm INVERT của chúng tôi đã biên soạn. Hi vọng qua bài viết này các bạn đã có thể hoàn toàn biết được orthocenter là gì cũng như giải các bài tập về orthocenter một cách dễ dàng.
999+ tài khoản GPT Chat miễn phí, Acc OpenAI Free đăng nhập thành công 100%
thẻ:
Trực tâm là gì?cách chứng minh trực giaotrực tâm của tam giác vuông

