Trực tâm của tam giác là giao điểm của ba đường cao của tam giác. Đây là điểm đặc biệt của tam giác. Vì vậy, nó sẽ có các thuộc tính đặc biệt. Bài viết dưới đây sẽ cung cấp thông tin Trúc Tâm là gì? Tính chất và cách xác định trực tâm của tam giác? Mời các bạn tham khảo.
Đầu tiên. Nêu khái niệm trực tâm của tam giác?
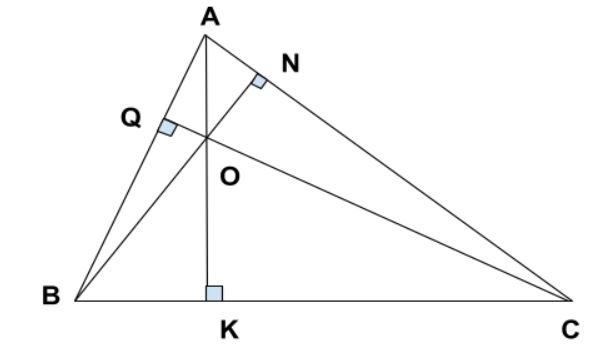
Trực tâm của một tam giác là điểm trùng với giao điểm của ba đường cao trong tam giác đó. Đường cao trong tam giác là đoạn thẳng nối một đỉnh của tam giác với đỉnh đối diện sao cho tạo thành một góc vuông. Cạnh đối diện với đường cao gọi là đáy của đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy của đường cao đó. Trực tâm của tam giác là giao điểm của ba đường cao trong tam giác. Tuy nhiên để xác định trực tâm không nhất thiết phải vẽ cả 3 đường cao mà chỉ cần vẽ 2 đường cao của tam giác về 2 cạnh đối diện. Hai đường cao này sẽ cắt nhau tại trực tâm của tam giác.
Với các dạng tam giác thông dụng như tam giác nhọn, tam giác tù, tam giác cân và tam giác đều, chúng ta đều có chung một cách xác định trực tâm. Từ hai đỉnh của tam giác kẻ hai đường cao đối với hai cạnh đối diện. Giao điểm của hai đường cao này là trực tâm của tam giác, còn đường cao kia chắc chắn đi qua trực tâm mặc dù ta không cần vẽ.
Việc xác định trực tâm của một tam giác không phải dựa vào mắt thường mà dựa vào các tính chất toán học của tam giác. Nếu trong một tam giác có ba đường cao cắt nhau tại một điểm thì điểm đó nhất định là trực tâm của tam giác.
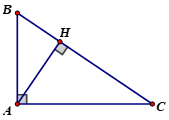
Đây là một ví dụ về trực tâm của một tam giác:
Ta có: H là trực tâm của tam giác ABC.
2. Cách xác định trực tâm của tam giác:
Để xác định trực tâm của một tam giác, ta có thể tìm giao điểm của ba đường cao của tam giác. Tuy nhiên, chỉ cần vẽ hai đường cao của tam giác là ta xác định được trực tâm. Trong trường hợp các tam giác như tam giác nhọn, tam giác tù, tam giác cân, tam giác đều, ta có thể kẻ hai đường cao kẻ từ hai đỉnh của tam giác đến hai cạnh đối diện. Trực tâm của tam giác được xác định tại giao điểm của hai đường cao này. Đường cao còn lại cũng phải đi qua trực tâm của tam giác, mặc dù không cần vẽ. Tuy nhiên đối với tam giác vuông thì trực tâm trùng với đỉnh của góc vuông vì hai cạnh tạo thành góc vuông cũng chính là các đường cao của tam giác.
Trực tâm của các tam giác khác nhau:
+ Trực tâm của tam giác nhọn – trực tâm nằm trong miền của tam giác nhọn.
+ Trực tâm của tam giác vuông – Trực tâm là đỉnh của góc vuông.
+ Trực tâm của tam giác tù – Trực tâm của tam giác tù nằm ngoài tam giác.
3. Tính chất của trực tâm:
Trực tâm trong tam giác có nhiều tính chất đặc biệt sau:
Tính năng 1: Trong một tam giác cân, đường trung trực của đáy là đường phân giác, đường cao và trung tuyến.
Tính năng 2: Nếu đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
Tính năng 3: Nếu đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
Tính năng 4: Trực tâm của tam giác nhọn trùng với tâm đường tròn nội tiếp tam giác có ba đỉnh là chân của ba đường cao kẻ từ các đỉnh đến các cạnh đối diện.
Tính năng 5: Đường cao ứng với một đỉnh của tam giác cắt đường tròn ngoại tiếp tại điểm thứ hai sẽ là phép đối xứng của trực tâm qua cạnh tương ứng.
Từ các tính chất trên ta suy ra rằng trong một tam giác đều thì trực tâm, trọng tâm, điểm nằm trong tam giác, điểm cách đều ba đỉnh và ba cạnh đều là một điểm.
4. Bài tập về trực tâm của tam giác:
4.1. Bài tập trắc nghiệm:
Câu hỏi 1: Đưa cho ΔABC cân tại A, các đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔTam giác MED là gì?
A. Tam giác cân
B. Tam giác vuông cân
C. Tam giác vuông
D. Tam giác đều.
Trả lời: A
Câu 2: Cho AB và điểm M nằm giữa A và B (MA < MB). Vẽ tia Mx vuông góc với AB, trên đó lấy hai điểm C, D sao cho MA = MC, MD = MB.
Tia AC cắt BD tại E. Tính số đo góc
A. 300
B. 450
C. 600
D.900
Trả lời: DỄ DÀNG
Bài 3: Đưa cho ΔABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Chọn phát biểu đúng:
MỘT. ΔABO = ΔCOE
b. ΔBOA = ΔCOE
C. ΔAOB = ΔCOE
Đ. ΔABO = ΔCEO
Xét các tam giác AOB và COE có
+ OA = OC (vì O thuộc đường trung trực của AC )
+ OB = OE (vì O thuộc tia phân giác của BE )
+ AB = CE (giả thiết)
Do đó AOB = COE (ccc)
Chọn đáp án C
4.2. Bài tập tự luận và lời giải:
Bưu kiện Đầu tiên:
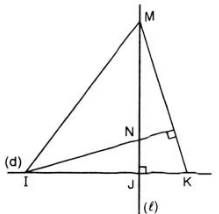
Trên đường thẳng d lấy ba điểm phân biệt I, J, K (J nằm giữa I và K).
Vẽ đường thẳng l vuông góc với d tại J. Trên l lấy một điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Giấy chứng nhận kỹ năng ⊥ TÔI.
PHẦN THƯỞNG
Vẽ hình minh họa:
Trong một tam giác, ba đường cao đồng quy tại một điểm là trực tâm của tam giác.
l ⊥ d tại J và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.
N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.
IN và MJ cắt nhau tại N .
Theo tính chất ba đường cao thì tam giác ⇒ N là trực tâm của ΔMKI.
⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.
Vì vậy, KN IM.
Bài 2: Giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh của góc vuông và trực tâm của tam giác tù nằm ngoài tam giác đó.
PHẦN THƯỞNG
+ Xét ΔABC vuông tại A
AB AC ⇒ AB là đường cao của cạnh AC và AC là đường cao của cạnh AB
hay AB, AC là các đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh của góc vuông
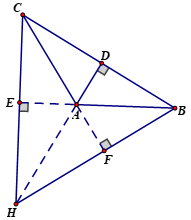
+ Xét ΔABC có góc tù A, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B thì
Vậy E nằm ngoài A và B
⇒ Tia CE nằm ngoài tia CA và tia CB ⇒ Tia CE nằm ngoài ΔABC.
+ Tương tự ta có tia BF nằm ngoài ΔABC.
+ Trực tâm H là giao điểm của BF và CE ⇒ H nằm ngoài ΔABC.
Vậy: trực tâm của tam giác tù nằm ngoài tam giác.
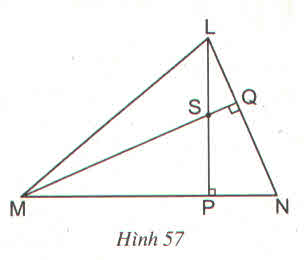
Bài 3: Cho hình
a) Chứng minh NS LM
b) Khi góc LNP = 50o, tính góc MSP và góc PSQ.
câu trả lời gợi ý
a) Trong ∆MNL có:
LP ⊥ MN nên LP là đường cao của ΔMNL.
MQ ⊥ NL nên MQ là đường cao của ΔMNL.
Mà LP, MQ cắt nhau tại điểm S
Vậy: theo tính chất ba đường cao của một tam giác thì S là trực tâm của tam giác.
⇒ SN là đường cao của ΔMNL.
hoặc SN ⊥ML.
b)
+ Ta có: trong một tam giác vuông hai góc nhọn phụ nhau nên:
ΔNMQ vuông tại Q có:
6. Bài tập tự luyện:
Bài 1: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Chỉ ra các đường cao của tam giác HBC. Sau đó chỉ cho ta trực tâm của tam giác đó.
Bài 2: Cho tam giác ABC có các đường cao AD, BE, CF. Trực tâm H.DF cắt BH tại M, DE cắt CH tại N. Chứng minh đường thẳng đi qua A và vuông góc với MN đi qua tâm ngoại tiếp tam giác HBC.
Bài 3: Cho tam giác ABC có trực tâm H. Chứng minh rằng các điểm đối xứng với H qua đường thẳng chứa các cạnh hoặc trung điểm của các cạnh nằm trên đường tròn (ABC).
Bài 4: Cho đường tròn (O, R), gọi BC là một dây cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.
Bài 5: Đưa cho △ABC có các đường cao AD,BE,CF cắt nhau tại HI; J lần lượt là trung điểm của AH và BC.
a) Chứng minh: IJ EF
b) Chứng minh: IE JE
Bài 6: Cho △ABC có các đường cao AD,BE,CF cắt nhau tại HI; J lần lượt là trung điểm của AH và BC.
a) Chứng minh: JT⊥EFJT⊥EF
b) Chứng minh: IE⊥JEIE⊥JE
c) Chứng minh: DA là tia phân giác của góc EDF.
d) Gọi P và Q là hai điểm đối xứng của D qua AB và AC .
Chứng minh: P; F; E; Q thẳng hàng.
Bài 7: Cho tứ giác lồi ABCD có ba góc bằng nhau tại các đỉnh A, B, C. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh O, H, D thẳng hàng.
Bài 8: Cho tam giác ABC có trực tâm H. Chứng minh rằng các điểm đối xứng với H qua đường thẳng chứa các cạnh hoặc trung điểm của các cạnh nằm trên đường tròn (ABC).
Bài 9: Cho tam giác ABC có các đường cao AD, BE, CF. Trực tâm H.DF cắt BH tại M, DE cắt CH tại N. Chứng minh đường thẳng đi qua A và vuông góc với MN đi qua tâm đường tròn ngoại tiếp tam giác HBC.
Bài 10: Cho tam giác ABC có H là trực tâm. P là một điểm bất kỳ trong tam giác đó. Gọi A1B1C1 là tam giác đạp của P với tam giác ABC. Trên HA, HB, HC lấy các điểm để có thể , , . Chứng minh tam giác ABC đồng dạng với tam giác